పరిచయము
ఈమధ్య పారసీక/ఉర్దూ ఛందముల ప్రక్రియలైన రుబాయీలపై, గౙలులపై ఈమాటలో వ్యాసములను వ్రాసినాను. అక్కడ ఒక విషయమును ప్రత్యేకముగా తెలిపినాను; అదేమనగా ఈ ఛందములలో రెండుకన్న లఘువులు పక్కపక్కన ఉండవని. అనగా న-గణము ఛందములో ఎక్కడ కూడ కనిపించదు. ఉదా: సుమన అని వ్రాసినను సుమన్ అని పలుకుట వలన అది లగము అవుతుంది కాని, న-గణము కాదు.
ట్రిబొనాచ్చి సంఖ్యలు
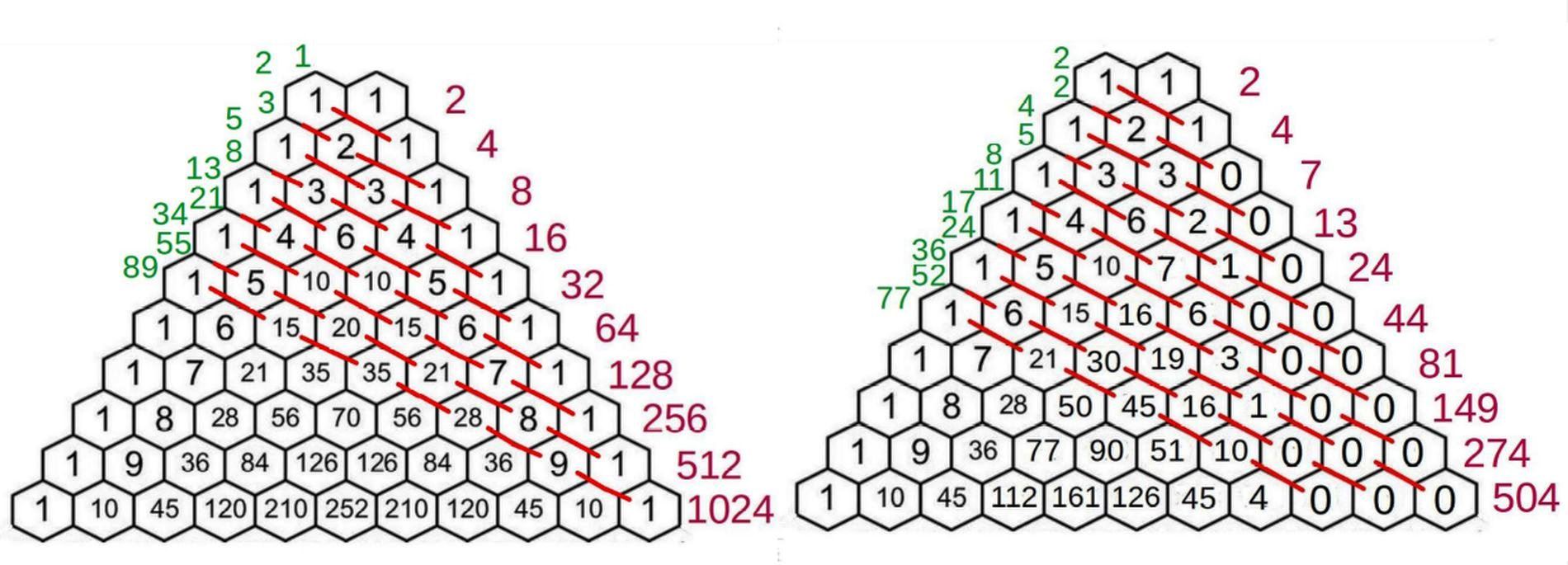
ఏడు అక్షరముల వఱకు గల వృత్తముల అమరికలను మొదటి పట్టికలో చూడ వీలగును. పట్టికలోని సంఖ్యలు 2, 4, 7, 13, 24, 44, 81… ఈ సంఖ్యలను గమనిస్తే ఒక ఆసక్తికరమైన విషయము గోచరిస్తుంది. మొదటి మూడు సంఖ్యలను చేర్చినప్పుడు నాలుగవ సంఖ్య లభిస్తుంది. రెండు నుండి నాలుగు వఱకు సంఖ్యలను కూడిక చేసినప్పుడు ఐదవ సంఖ్య లభిస్తుంది. అనగా nm = n(m-1) + n(m-2) + n(m-3). ఇంతకు ముందు విరహాంకుని సంఖ్యలు లేక ఫిబొనాచ్చి సంఖ్యలను మాత్రా ఛందస్సు వివరణలో చర్చించి యున్నాను. అవి nm = n(m-1) + n(m-2) సమీకరణమును పాటిస్తుంది. పైన చూపిన nm = n(m-1) + n(m-2) + n(m-3) సంఖ్యలకు ట్రిబొనాచ్చి సంఖ్యలు (Tribonacci numbers) అని పేరు. ట్రిబొనాచ్చి అనే ఏరుతో ఏ వ్యక్తియు లేడు. ఇది కేవలము కాల్పనికము మాత్రమే. ఈ ట్రిబొనాచ్చి సంఖ్యలను మొట్టమొదట అగ్రనోమోఫ్ అను శాస్త్రజ్ఞుడు 1914లో ప్రస్తావించెను. కాని అంతకుముందే ఏనుగుల జనసంఖ్యను వివరించుటకై ఛాల్స్ డార్విన్ (Charles Darwin) తన కొడుకైన జార్జ్ హోవర్డ్ డార్విన్ (George Howard Darwin) ప్రతిపాదించిన సిద్ధాంతమును గ్రహించెను. ఇది ఒక మేధోప్రహేళిక (gedenken; thought experiment). ఒక ఆడ ఏనుగు, ఒక మగ ఏనుగు – ఈ రెండింటిని ఒక ఏనుగు జంట అని పిలుద్దాము. ఈ ఏనుగు జంటలు 30, 60, 90 ఏండ్లకు ఆడ మగ ఏనుగులను కంటాయి. 90 ఏళ్ళకు పిదప అవి కొత్త ఏనుగులను కనవు. ఒక్కొక్క తరములో (generation) ఎన్ని కొత్త ఆడమగ ఏనుగుల జంటలు పుట్టాయి అన్నది ఇక్కడ ప్రశ్న[1].
0 → A, 30 → (A) + B,
60 → (A+B) + 2C, 90 → (A+B+2C) + 4D,
120 → (B+2C+4D) + 7E, 150 →(2C+4D+7E) + 13F
180 → (4D+7E+13F) + 24G, 210 → (7E+13F+24G) + 44H,
240 → (13F+24G+44H) + 81I, 270 → (24G+44H+81I) + 149J ….
ప్రతి తరములో జన్మించిన కొత్త జంటలు (B, C, D,… ఇత్యాదులు) 1, 2, 4, 7, 13, 24, 44, 81, 149 …. ఈసంఖ్యలు nm = n(m-1) + n(m-2) + n(m-3) సమీకరణమునకు సరిపోతాయి.
ఫిబొనాచ్చి సంఖ్యలు ఏవిధముగా x2 – x – 1 = 0 వర్గ సమీకరణపు (quadratic equation) పరిష్కారములుగా ఉండే φ మఱియు (1- φ) లకు సంబంధము కలిగి ఉన్నవో, అదే విధముగా ట్రిబొనాచ్చి సంఖ్యలు x3 – x2 – x – 1 = 0 ఘన సమీకరణపు (cubic equation) పరిష్కారములు. ఇందులో ఒకటి మాత్రమే వాస్తవము (real), మిగిలిన రెండు సంకీర్ణములు (complex). φ విలువ కరణీయ సంఖ్యయైన (irrational number) 1.6180339887… = (1 + √5)/2. ట్రిబొనాచ్చి సంఖ్యల సమీకరణపు పరిష్కారములు ɳ = 1.83928675521…, -0.4196433776… + im 0.6062907292…, -0.4196433776… – im 0.6062907292… (im = √-1); ɳ = [1 + 3√(19 – 3. √33) + 3√(19 + 3. √33)]/3,
ఈ ట్రిబొనాచ్చి స్థిరాంకము (ట్రిబొనాచ్చి constant ɳ) ఖగోళసృష్టి శాస్త్రము (cosmology)[2], స్నబ్ క్యూబ్ (snub cube), రౌజీ ఫ్రాక్టల్స్ (Rauzy fractals) మున్నగు చోటులలో కనబడుతుంది. ఛందఃశాస్త్రములో దీని పాత్రను మాత్రమే ఇక్కడ నేను చర్చిస్తాను. పైన చెప్పినట్లు 0, 0, 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, 274, 504, 927, 1705, 3136, 5768, 10609, 19513, 35890, … సంఖ్యలు ట్రిబొనాచ్చి సంఖ్యలు. అక్షర ఛందస్సు ప్రస్తావనలో అక్షరమేరు (Pascal Triangle) నిర్మాణమును గుఱించి వివరించినాను. ఇప్పుడు ఈ ట్రిబొనాచ్చి అంకెలకు పాస్కల్ త్రికోణమువంటి త్రికోణ నిర్మాణమును గుఱించి చర్చిస్తాను. ఈమేరువును త్రిమేరు అని పిలువ దలచినాను.
ట్రాస్కల్ త్రికోణము
మొదటి చిత్రములో ఎడమవైపు పాస్కల్ త్రికోణమును (అక్షరమేరువు), కుడివైపు నేను నిర్మించిన ట్రాస్కల్ త్రికోణము (త్రిమేరు) చూపబడినవి. ఈ చిత్రములో పది పంక్తులు గలవు. ఉదాహరణముగా ఏడవ పంక్తిని తీసికొందాము. పాదమునకు ఏడు అక్షరములు గల వృత్తములు మొత్తము 27 = 128. ఇందులో ఏడు గురువులు ఉన్నది 1 వృత్తము, ఆఱు గురువులు, ఒక లఘువుతో వృత్తములు 7, ఐదు గురువులు, రెండు లఘువులతో వృత్తములు 21, నాలుగు గురువులు, మూడు లఘువులతో వృత్తములు 35, మూడు గురువులు, నాలుగు లఘువులతో వృత్తములు 35, రెండు గురువులు, ఐదు లఘువులతో వృత్తములు 21, ఒక గురువు, ఆఱు లఘువులతో వృత్తములు 7, ఏడు లఘువులతో వృత్తము 1. ఇవి ద్విపద సిద్ధాంతము (binomial theorem) (a+b)7లో am.b(7-m)ల గుణకములు (coefficients). వీటిని కలిపితే మనకు ఆ ఛందములోని మొత్తము వృత్తముల సంఖ్య 128 లభిస్తుంది. కుడివైపు ఉండే త్రికోణమునకు కూడ వివరణ యిదియే. కాని ఇక్కడ రెండింటికన్న, అనగా 3 నుండి 7 లఘువులు గల వృత్తములు పరిగణించబడవు. అప్పుడు మనకు లభించు వృత్తములు వరుసగా: 1, 7, 21, 30, 19, 3, 0, 0. వీటి మొత్తము 81. ఈ 81 ముందున్న మూడు సంఖ్యలను, అనగా 13, 24, 44, కలిపినప్పుడు మనకు లభిస్తుంది.
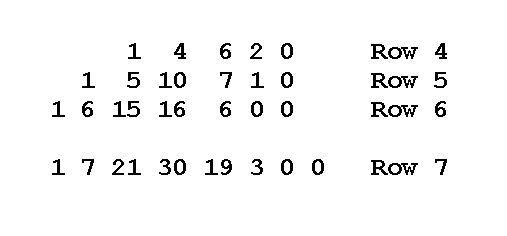
అంతే కాక ఈ 1, 7, 21, 30, 19, 3, 0, 0 సంఖ్యలు ముందున్న మూడు పంక్తులలోని సంఖ్యలను కుడివైపు అమర్చి వాటిని కలిపి చివర ఒక సున్నను ఉంచితే లభిస్తుంది. దానిని రెండవ చిత్రములో చూడ వీలగును. ఇది కూడ ట్రిబొనాచ్చి సిద్ధాంతమే! పాస్కల్ త్రికోణములో ఎఱ్ఱటి రంగుతో ఉండే సరళరేఖలను కలిపితే మనకు లభించు సంఖ్యలు 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, .., ఇత్యాదులు ఫిబొనాచ్చి లేక విరహాంక సంఖ్యలు. ఇవి 1, 2, 3, 4, 5, … మాత్రలు ఎన్ని విధములుగా ఉండునో అనే విషయమును తెలుపుతుంది, ఉదాహరణముగా ఐదు మాత్రలు ఎనిమిది విధములుగా సాధ్యము. అదేవిధముగా ట్రాస్కల్ త్రికోణములో (త్రిమేరులో) ఈ సంఖ్యలు 2, 2, 4, 5, 8, 11, 17, 24, 36, 52, …, ఇత్యాదులు. ఇవి కూడ 1, 2, 3, 4, 5, … మాత్రలు ఎన్ని విధములుగా ఉండునో అనే విషయమునే తెలుపుతుంది, కాని ఈమాత్రలలో రెండింటికన్న ఎక్కువగా లఘువులు ఉండవు. ఉదాహరణముగా ఎనిమిది విధములైన ఐదు మాత్రలలో (IUU, UIU, UUI, IIIU, IUII, IIUI, UIII, IIIII) IIIU, UIII, IIIII మాత్రలలో మూడు లఘువులు ఉన్నాయి కనుక ఇవి నిషిద్ధము, కావున ఇందులో మొత్తము పంచమాత్రలు ఐదే! మఱొక విచిత్రము ఏమంటే ఈ 2, 2, 4, 5, 8, 11, 17, 24, 36, 52, … కూడ ట్రిబొనాచ్చి సంఖ్యలే. కాని ఇవి ముందున్న మూడింటిని కలిపితే రాదు. ముందున్న సంఖ్యను వదలి, దానికి ముందున్న మూడింటిని కలిపితే ఈసంఖ్యలు లభిస్తాయి. అనగా nm = n(m-2) + n(m-3) + n(m-4).
ముగింపు
పారసీక ఛందస్సులో పాదములో ఎక్కడైనను మూడు లఘువుల ఉనికి నిషిద్ధము. దీనివెనుక ఉన్న గణిత సిద్ధాంతమును మొట్టమొదటిసారిగా నేను ట్రిబొనాచ్చి సంఖ్యల ద్వారా వివరించినాను. అక్షరమేరువులోని విరహాంక సంఖ్యలవలె, నేను కల్పించిన ట్రాస్కల్ త్రికోణము లేక త్రిమేరువులో కూడ మూడు లఘువులు లేని మాత్రల సంఖ్య ప్రత్యక్షమవుతుంది.
గ్రంథసూచి
- How fast does Darwin’s elephant population grow? – Janos Podani, Adam Kun and Andras Szilagyi – Journal of the History of Biology, 2017, DOI 10.1007/s10739-017-9488-5.
- Tribonacci Quantum Cosmology – Angus McCoss, Journal of Quantum Information Science, 2019, 41-97.