సంగ్రహము

ప్రాచీన భారతీయ గణితశాస్త్రములో కనుగొనబడిన విశేషాలలో కొన్ని ఛందశ్శాస్త్ర మార్గములో మనకు లభించినవి. యుగ్మాంకగణితము (binary arithmetic), ద్విపద సిద్ధాంతము (binomial theorem), మేరు నిర్మాణము (Pascal triangle), విరహాంక సంఖ్యలు (Fibonacci numbers) పింగళ, హలాయుధ, విరహాంక, గోపాల, హేమచంద్రాదుల అధ్యయన ఫలితమే. షట్ప్రత్యయాలీ సిద్ధాంతముల అంశములను వివరిస్తాయి. అనంతామాత్యుడు ఛందోదర్పణములో వీటిని చక్కగా విశదీకరిస్తాడు. మాత్రాఛందస్సు గురించి ప్రాకృత హిందీ భాషలలో నెక్కువగా వ్రాయబడియున్నను తెలుగులో వీటి చర్చ చాల పరిమితమే. కన్నడ తెలుగు భాషలలోని దేశి ఛందస్సులో అంశ లేక ఉపగణములను ఉపయోగిస్తారు. తెలుగులోని సూర్యేంద్రచంద్రగణములు కన్నడమునందలి బ్రహ్మ విష్ణు రుద్ర గణములనుండి పుట్టినవే. కాని వీటియొక్క మేరునిర్మాణమును గురించిన వ్యాఖ్యలు లేవు. వీటి మేరునిర్మాణము ఇక్కడ ప్రప్రథమముగా చర్చించదలిచాను. అంతే కాదు, యీ సిద్ధాంతమును సార్వత్రీకరించి క్రొత్త క్రొత్త గణములను, ఛందస్సును సృష్టించుటకు వీలగునని నిరూపించడానికి ప్రయత్నించాను.

పరిచయము

భారతీయ గణితశాస్త్రములో కొన్ని నూతనాంశములు ఛందశ్శాస్త్రము ద్వారా వెలుగులోనికి వచ్చాయి. నేడు మనము కంప్యూటరులలో ఉపయోగించే యుగ్మగణిత (binary arithmetic) సిద్ధాంతములు, పరిక్రియలు రెండు వేల సంవత్సరములకు ముందు వాడుకలో నున్నవే. నేడు మనము ఫిబనాచ్చీ శ్రేణి అని పిలిచే సంఖ్యలు సుమారు ఆఱవ శతాబ్దములో భారతదేశములో కనుగొనబడ్డాయి. అక్షర గణములు, మాత్రా గణములు, వీటితో నిర్మించబడిన అక్షర వృత్తములు, మాత్రా వృత్తములు అన్ని భాషలలో కవులచే ఉపయోగించబడినవే. ఇవిగాక కన్నడ తెలుగు భాషలలో అంశ లేక ఉపగణములచే అమర్చబడిన అక్కఱ, ద్విపద, రగడలాటి జాతి పద్యములు, సీసము, ఆటవెలది, తేటగీతివంటి ఉపజాతులకు చెందిన పద్యములు దేశి ఛందస్సు ప్రత్యేకత. ఈ వ్యాసపు ముఖ్యోద్దేశము యీ గణితాంశములపై మనకు ఇంతవఱకు పరిచితమైన విషయాల విశేషాలను తెలుపుట. అంశ లేక ఉపగణములపై నేను కనుగొన్న కొన్ని క్రొత్త విషయాలను, వాటిని ఉత్పత్తి చేసే విధానమును కూడ వివరించ ప్రయత్నిస్తాను.

పద్యములు గణసముదాయములు. గణములు కొన్ని అక్షరములచే నిర్మింపబడినవి. భారతీయ ఛందశ్శాస్త్రములో మనము ఎదుర్కొనే గణములు – అక్షర గణములు, మాత్రా గణములు, అంశ లేక ఉపగణములు, తమిళ ఛందస్సులోని శీరులు. అక్షర గణములు తమిళము తప్ప దాదాపు అన్ని భారతీయ భాషలలో ఉన్నాయి. సంస్కృత ఛందస్సులో మూడు అక్షరములకన్న ఎక్కువగా ఉండే గణములు లేవు. ఈ గణములను వరుసగా మొదటి పట్టికలో చూడవచ్చు. వీటిని గుర్తించడానికి య-మా-తా-రా-జ-భా-న-స-ల-గం అనే ఒక కొండ గుర్తును ఉపయోగిస్తారు. మూడు మూడక్షరములుగా తీసుకొంటే, ఆ గణపు పేరు దానికి మొదట ఉంటుంది, ఉదా. మాతారా – మ-గణము. పై సూత్రమునకు బదులు జ-రా-య-మా-తా-భా-న-స-ల-గం అనే సూత్రమును కూడ వాడవచ్చునని ఒకటి ఉంది. గురువుకు 0, లఘువుకు 1 సంఖ్యను నియోగించినప్పుడు, ఈ గణములు యుగ్మ సంఖ్యలకు (binary numbers) అమరిక అవుతుంది. ప్రాచీన భారతీయ గణితశాస్త్రములో నేటిలా కాక కనిష్ఠ సంఖ్యను ఎడమవైపు, గరిష్ఠ సంఖ్యను కుడివైపు ఉంచుతారు. మూడింటికన్న ఎక్కువగా అక్షరములు ఉన్నప్పుడు, వాటిని ఈ మూడక్షరాల గణములతో వివరిస్తారు, ఉదా. UUIIU – త-ల-గ (తెలుగులో దీనిని త-వ అని కూడ అంటారు), UUIUI – త-గ-ల (తెలుగులో దీనిని త-హ అని కూడ అంటారు). ఈ మూడక్షరాల గణములనే రెండువేల సంవత్సరాలుగా లాక్షణికులు ఉపయోగిస్తున్నారు. ఒకరిద్దరు దీనికి భిన్నముగా గణములను వివరించియున్నారు (మొదటి పట్టిక), కాని ఇవి సర్వజనామోదమును పొందలేదు.

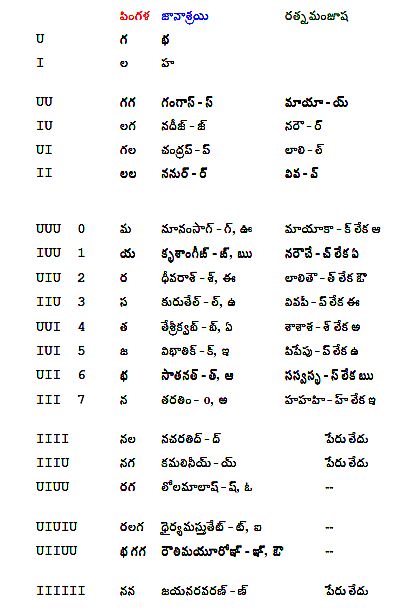
మొదటి పట్టిక – గణములు: ఇందులో U గురువుకు గుర్తు, I లఘువుకు గుర్తు. పింగళ ఛందస్సులోని గణములు ఎడమవైపు, జానాశ్రయిలో^[15] పేర్కొనబడిన గణములు మధ్య వరుసలో, రత్నమంజూషలో^[16] పేర్కొనబడిన గణములు కుడివైపు చూపబడ్డాయి. త్రిక గణములైన మ, భ, జ, స, న, య, ర, త లకు వాటి యుగ్మగణితాంకములు కూడ చూపబడ్డాయి. జానాశ్రయి కర్త గుణస్వామి సహాయముతో వ్రాసిన మాధవవర్మ (క్రీ. శ. 580-620) తాను పేర్కొన్న గణములకు హలంతములతో, అచ్చులతో పేర్లు పెట్టాడు. ఉదాహరణకు మ-గణమును గ్ అనియు లేక ఊ అనియు పేర్కొన్నాడు. అజ్ఞాతుడైన రత్నమంజూష రచయిత (ఇతడు హేమచంద్రునికన్న ముందున్న వాడు) అదే మ-గణమును క్ లేక ఆ అని పిలిచాడు.

షట్ప్రత్యయములు

ఛందశ్శాస్త్రములోని గణితాంశములను షట్ప్రత్యయములు నిరూపిస్తాయి. ప్రస్తారము, నష్టలబ్ధి, ఉద్దిష్టము, వృత్త సంఖ్య, లగ క్రియ, అధ్వము – ఈ ఆఱింటిని షట్ప్రత్యయములు అంటారు. అక్షరములు రెండు విధములు – గురువు, లఘువు. సంయుక్తాక్షరము ముందున్న అక్షరము, పొల్లుతో కూడిన అక్షరము (ఉదా. ద్రుతప్రకృతికము), బిందుయుక్త అక్షరము, ప్లుతము (సాగించి పలికే అక్షరములు) దీర్ఘాక్షరముతో కూడ గురుతుల్యమే. ఒక అక్షరము గురువుగానో లేక లఘువుగానో మాత్రమే పరిగణించబడుతుంది. ఈ షట్ప్రత్యయ వివరాలు చక్కగా అనంతామాత్యుని ఛందోదర్పణములో^[1,2] తెలుపబడ్డాయి.

వృత్త సంఖ్య

కొన్ని అక్షరముల (n) వృత్త పాదము ఒకటి ఉండినప్పుడు, అందులో ఎన్ని వృత్తములు జనింపగలవన్న మొదటి ప్రశ్న వృత్త సంఖ్య. దాని జవాబు – 2 ను 2 తో ఆ అక్షరముల సంఖ్య(n) యెంతో అన్ని సార్లు గుణించగా వచ్చే సంఖ్య, 2ⁿ. ఒక వృత్త పాదములో ఆఱు అక్షరములు ఉండినప్పుడు, మనకు 2.2.2.2.2.2 = 64 వృత్తములు, అనగా 2⁶ వృత్తములు లభిస్తాయి.

ప్రస్తారము

ఇక రెండవ ప్రశ్న – అందులో గురులఘువుల అమరికలు ఏలాగుంటాయి? దీనినే ప్రస్తారము అంటారు. దీనికి జవాబు ఆఱు అక్షరాల వృత్తాల పట్టికలో (రెండవ పట్టిక) చూడ వీలవుతుంది. మొదట అన్ని అక్షరములు గురువులుగా వ్రాయాలి. తరువాత రెండవ పంక్తిలో ఎడమవైపు గురువు క్రింద లఘువును ఉంచి కుడివైపు అక్షరములను అలాగే ఉంచి వ్రాయాలి. ఎడమవైపు లఘువులను గురువులుగా వ్రాయాలి. 6 అక్షరముల వృత్తములలో మొదటిది UUUUUU, రెండవది IUUUUU, మూడవది UIUUUU. ఇలాగే మనము గురులఘువులను మార్చుకొని వ్రాస్తూ వెళ్ళితే, చివరి వృత్తము IIIIII అవుతుంది. UUUUUU వృత్తపు యుగ్మాంకము 0, IIIIII వృత్తపు యుగ్మాంకము 63. వీటికి ఒకటి సంఖ్యను కూడిస్తే మనకు వృత్తపు సంఖ్య దొరుకుతుంది.

మూడవ, నాలుగవ ప్రశ్నలు – ఒక వృత్త సంఖ్యకు గురులఘువుల అమరిక, ఒక గురులఘువుల అమరికకు సరిపోయే వృత్త సంఖ్య ఏ విధముగా పొందుటకు వీలవుతుంది? మొదటి ప్రక్రియను నష్టలబ్ధి అని, రెండవ ప్రక్రియను ఉద్దిష్టము అని అంటారు.

నష్టలబ్ధి

వృత్త సంఖ్యనుండి ఒకటి తీసివేసినప్పుడు వచ్చిన సంఖ్యను యుగ్మాంకముగా వ్రాసి, అందులోని శూన్య సంఖ్యలను గురువుచే, ఏక సంఖ్యను లఘువుచే మార్చగా వచ్చే అమరిక ఆ వృత్తపు గురులఘువుల అమరికను తెలుపుతుంది. ఉదాహరణకు జగతీఛందములో 1171వ వృత్తపు గురులఘువుల అమరిక ఏలాగుంటుంది? 1171 సంఖ్యనుండి 1 తీసివేయగా 1170 మనకు లభిస్తుంది. దశాంశ సంఖ్య 1170 యొక్క యుగ్మాంకము 010010010010 కాబట్టి దీని గురు లఘువులు – UIUUIUUIUUIU, ఇది జగతీఛందములోని స్రగ్విణీ వృత్తము. దీనినే ఈ క్రింది విధముగా పొందవచ్చు: సంఖ్యను 2 అంకెతో విభజించి, అది బేసి సంఖ్య అయితే ఒకటి కలిపి మళ్ళీ ఒకటి సంఖ్య లభించువరకు విభజించాలి. ఎక్కడెక్కడ బేసి సంఖ్య వస్తుందో అక్కడ గురువును, మిగిలిన చోట లఘువును ఉంచితే ఆ వృత్తపు గురులఘువులు మనకు లభిస్తుంది. పై ఉదాహరణలో –

1171+1/2 = 586/2 = 293+1 = 294/2 = UIU

147+1 = 148/2 = 74/2 = 37+1 = 38/2 = UIU

19+1 = 20/2 = 10/2 = 5+1 = 6/2 = UIU

3+1 = 4/2 = 2/2 = 1+1 = 2/2 = 1 UIU

ఉద్దిష్టము

గురువులకు బదులు 0, లఘువులకు బదులు 1 సంఖ్యను ఉంచితే వచ్చిన యుగ్మాంకానికి సరిపోయే దశాంశ సంఖ్యకు ఒకటి చేరిస్తే ఆ గురులఘువుల అమరికకు సరిపోయే వృత్త సంఖ్య లభిస్తుంది. ఉదాహరణకు, పదవ ఛందములో రుక్మవతీవృత్తపు సంఖ్య ఏమి? రుక్మవతి గణములు UII UU UII UU. దీని యుగ్మాంకము 0110001100, అనగా దీని దశాంశ సంఖ్య 0+2+4+0+0+0+64+128+0+0 = 198. దీనికి ఒకటి చేరిస్తే వచ్చిన 199 రుక్మవతీ వృత్తపు సంఖ్య. ప్రతి పాదానికి పది అక్షరాలు ఉండే పంక్తి ఛందం ఈ వృత్తలక్షణం.