1. పరిచయము

నాకు చిన్నప్పటినుండి ముగ్గులంటే చాల యిష్టము. అమ్మగారు, యిద్దరు అక్కలు ముగ్గులు వేస్తుంటే చూడ ముచ్చటగా ఉండేది. చుక్కలను వరుస తప్పకుండా వంకరటింకరలు లేకుండా పెట్టి, వాటిని ఒకే దళసరిగా కలిపి ఒక చిత్రాన్ని పుట్టిస్తూ, అది ముగిసిన తరువాత చివరకు సంతృప్తితో దాని అందచందాలను చూడడము ఇంకా నా స్మృతిపథములో మెరుస్తూనే వుంది. బాల్యములో ముగ్గులు కలిగించిన ఈ ఆకర్షణ నన్ను యింకా వదలలేదు. దానికి ఒక ముఖ్యమైన కారణము నా వృత్తి. వృత్తి రీత్యా నేను ఒక స్ఫటిక శాస్త్రజ్ఞుడిని. స్ఫటిక శాస్త్రములో సామ్యరూపము (symmetry) లేక సౌష్ఠవపు పాత్ర యెంతో విలువైనది. ఒకే రకమైన చుక్కల అమరికతో ఎన్నో విధాలైన కొత్త కొత్త ముగ్గులను వేయడము ఆ కాలములో నాకు చాల సరదాగా ఉండేది. తరువాతి కాలములో అక్కడ భారతదేశములో, ఇక్కడ అమెరికాలో విద్యార్థులకు ఈ సౌష్ఠవపు సిద్ధాంతాలను బోధించే సమయములో ముగ్గులను వాడేవాడిని. గడచిన రెండు మూడు సంవత్సరాలుగా ముగ్గుల వ్యాసంగము ఎక్కువైనది. ఒక ముగ్గు అమరికను గణితశాస్త్రరీత్యా పరిశీలించి అర్థము చేసికొంటే అదే విధముగా ఎన్నో కొత్త కొత్త ముగ్గులను సృష్టించడానికి వీలవుతుంది. అలా చేయగా కలిగిన కొన్ని కొత్త అంశాలను పంచుకోవడమే ఈ వ్యాసపు ముఖ్యోద్దేశము. ఇక్కడ ఒక విషయము చెప్పుకోవాలి. నాకు చేతితో నేలపైన ముగ్గులను వేయడానికి రాదు. కాగితముపైన, కంప్యూటరుపైన మాత్రమే వేయగలను. సుమారు ఐదువందల ముగ్గులను, వాటి వెనుక ఉండే గణితాంశాలను ఐకోలం.కామ్ వెబ్‌సైటులో నా గ్యాలరీలో, బ్లాగులలో, కఫే వ్రాతలలో వివరించాను. పవర్‌పాయింట్, గింప్, పెయింట్, ఇర్ఫాన్‌వ్యూ వంటి సాఫ్ట్‌వేర్లను ఉపయోగించి ముగ్గులను వేస్తాను. నా యీ వ్యాసము చదవడానికి ముందు, ముగ్గులపైన, సౌష్ఠవ సిద్ధాంతాలపైన నేను వ్రాసిన రెండు వ్యాసాలు (కౌముదిలో, ఈమాటలో) చదివితే మంచిది.

2. ముగ్గుల ప్రాచీనత

ముగ్గులు, అందులో ప్రత్యేకముగా మెలిక ముగ్గులు చాల పురాతనమైనవి. సింధులోయ నాగరికత శిథిలాలలో హరప్పాలో యీ నాటి మెలిక ముగ్గులవంటి చిత్రాలను కనుగొన్నారు. మెలిక ముగ్గుల నమూనాలు ఎన్నో ఆలయాలలో స్తంభాలపైన చెక్కియున్నారు. తమిళనాడులోని యిప్పటి కరూరులో పదవ శతాబ్దములో చోళరాజులు కట్టిన పశుపతీశ్వరాలయపు శిల్పాలు యిందులకు తార్కాణము. దక్షిణ చెన్నైలోని తిరువాణ్మైయూరునందలి మరుందీశ్వరర్ (ఓషధీశ్వరుడు) గుడిలో కూడ మూడు త్రిభుజాలతో మెలిక ముగ్గులాటి శిల్పము ఒకటి ఉన్నది. దీనిని బొరోమీయన్ వృత్తాలకు ఉదాహరణగా చెబుతారు. ఇది కాక ఈజిప్టు, గ్రీకు శిల్పాలలో, సెల్టిక్ ముడులలో మెలిక ముగ్గులను బోలిన చిత్రాలు ఉన్నాయి. మధ్య ఆఫ్రికాలోని సోనా ముగ్గులలో, పసిఫిక్ సముద్ర ద్వీపమైన వనూఅటు (Vanuatu) ఇసుక ముగ్గులలో కూడ యిట్టి పద్ధతి ప్రతిబింబితమవుతుంది.

వినుకొండ వల్లభరాయని క్రీడాభిరామములో^[1] మాచల్దేవి చిత్రశాల ప్రవేశద్వారములో వేసిన ముగ్గు గురించి ఒక పద్యము ఉన్నది. అది:

చందనంబునఁ గలయంపి చల్లినారు
మ్రుగ్గు లిడినారు కాశ్మీరమున ముదమున
వ్రాసినా రిందు రజమున రంగవల్లి
కంజములఁ దోరణంబులు గట్టినారు

– వల్లభరాయడు, క్రీడాభిరామము – 178

గంధపు నీళ్ళతో కళ్ళాపి చల్లి, పసుపు కుంకుమలతో ఆనందముగా ముగ్గులు పెట్టారు. పొడితో రంగవల్లిని వ్రాశారు. తామరపూలతో తోరణాలు కట్టారు. ఈ పద్యములో నాకు మరొక విశేషము కనబడుతుంది. ముగ్గులను, రంగవల్లులను వేరువేరుగా ప్రస్తావించడము. అంటే కాకతీయుల కాలములోనే బహుశా చుక్కలుంచి పెట్టిన ముగ్గులకు, స్వతంత్రముగా తోచినట్లు పెట్టే రంగవల్లులకు (freehand drawing) తేడా ఉండినది కాబోలు. ఆ కాలములోని “రెడ్డొచ్చె రెడ్డొచ్చె రెడ్డొచ్చె నమ్మా” అనే ఒక జానపద గీతములో “చేకట్ల పసుపు కుంకుమా పూయించు రంగవల్లుల నూరు రాణింపజేయు” అని రంగవల్లి ప్రస్తావన ఉన్నది. ఈ పాటను, కింది పద్యాన్ని సురవరం ప్రతాపరెడ్డి^[2] పేర్కొన్నారు. విజయనగరసామ్రాజ్యములో బ్రాహ్మణుల యిండ్లను వర్ణిస్తూ శుకసప్తతిలోని ఒక పద్యము “అలికి మ్రుగ్గులు పెట్టినట్టి తిన్నెలు” అని ప్రారంభమవుతుంది. హంసవింశతిలోని మరో పద్యము కూడ బ్రాహ్మణుల యిండ్లలో తులసీ బృందావనమువద్ద పెట్టిన ముగ్గులను గురించి – “పంచవన్నియ మ్రుగ్గు పద్మము ల్నించిన బృందావనము లోఁగిలందె వెలయ” అని ఉన్నది. కృష్ణరాయని ఆముక్తమాల్యద^[3]లోని కింది పద్యము ఆ కాలములో గుడిలో ముగ్గు పెట్టే వాడుక ఉండేదని చెబుతుంది.

బోటి గట్టిన చెంగల్వపూవుటెత్తు
దరు పరిణతోరు కదళి మంజరియు గొనుచుఁ
బోయి గుడి నంబి విజనంబు జేయఁ జొచ్చి
మ్రొక్కి వేదికఁ బలువన్నె మ్రుగ్గుఁ బెట్టి

– శ్రీకృష్ణదేవరాయలు, ఆముక్తమాల్యద, 5-91.

పదిహేడవ శతాబ్దపు పూర్వభాగములో వ్రాయబడిన చేమకూర వేంకటకవి విజయవిలాసము^[4]లోని ఈ పద్యములో కూడ ముగ్గుల ప్రసక్తి ఉన్నది –

ఆణిమెఱుంగుముత్తెపుటొయారపు మ్రుగ్గులు, రత్నదీపికా
శ్రేణులు, ధూపవాసనలు, హృద్యనిరంతర వాద్యఘోషముల్
రాణఁ బొసంగఁ బ్రోలు మిగులం గనువిం దొనరించు నిత్యక-
ల్యాణముఁ బచ్చతోరణమునై జనులందఱు నుల్లసిల్లఁగన్

– చేమకూర వేంకటకవి, విజయవిలాసముం 1-18.

మంచన కేయూరబాహుచరిత్రములోని ఒక సీసపద్యములోని పంక్తి – “అసదృశ కుంకుమరసలిప్తతల పరవశిత ముక్తారంగవల్లికంబు” – వివాహమండపమును ఎలా ముగ్గులతో అలంకరించారో అనే విషయాన్ని తెలుపుతుంది. సీమంతినీకల్యాణము^[5]లో కూడ వివాహ మండపాన్ని వర్ణించే ఒక సీస పద్యములో – “కల్యాణవేదిపై ఘనవృత్తిఁ గ్రొత్త ముత్తెపు రంగవల్లికల్ దీర్చువారు,” అని రంగవల్లి ముచ్చట ఉన్నది.

3. మెలిక ముగ్గులు

ముగ్గులను రెండు రకాలుగా విడదీయవచ్చును – ఒకటి చుక్కలు పెట్టి ముగ్గులు వేయడము, మరొకటి చుక్కలు లేకుండా రంగులు నింపి (freehand drawing) వర్ణచిత్రాలుగా వేయడము. చుక్కల ముగ్గులలో కూడ కొన్ని ముగ్గులలో చుక్కలను కలుపుతారు. ఇట్టి ముగ్గులకు చుక్కలు కేవలము ఒక మార్గదర్శి లేక దిక్సూచిక మాత్రమే. మరి కొన్ని ముగ్గులలో గీతలు చుక్కలను చుట్టుకొని ఒక దానిని మరొకటి ఖండించుకొంటూ ఉంటాయి. ఇట్టి ముగ్గులను మెలిక ముగ్గులు (తమిళములో చిక్కు కోలము) అంటారు. కొన్ని మెలిక ముగ్గులు చుక్కలు లేకుండా కూడా ఉంటాయి. నా యీ వ్యాసములో యీ మెలికముగ్గులను గురించి మాత్రమే చర్చిస్తాను.

4. సోనా ముగ్గులు

సుమారు రెండు సంవత్సరాలకు ముందు నాకు సోనా ముగ్గులతో పరిచయము అయినది. ఈ రంగములో నా కృషికి ఆ సంఘటన యెంతో దోహదకారి అయినదని చెప్పుటలో అతిశయోక్తి లేదు. మధ్య ఆఫ్రికాలో అంగోలా, జాంబియా, జైర్ (కాంగో) దేశాల సరిహద్దులలో చాక్వే అనే ఆదిమజాతివారు ఈ సోనా ముగ్గులను తరతరాలుగా చిత్రించేవారు, అంతేకాదు ఒక్కొక చిత్రానికి ప్రత్యేకమైన ఒక కథను కూడా అల్లేవారు. దీనిని నేర్పడానికి గురువులు ఉండేవారు. సామాన్యముగా యీ ముగ్గులలో ప్రావీణ్యాన్ని మగవాళ్ళు మాత్రమే గడించేవారు.

1. సోనా ముగ్గు

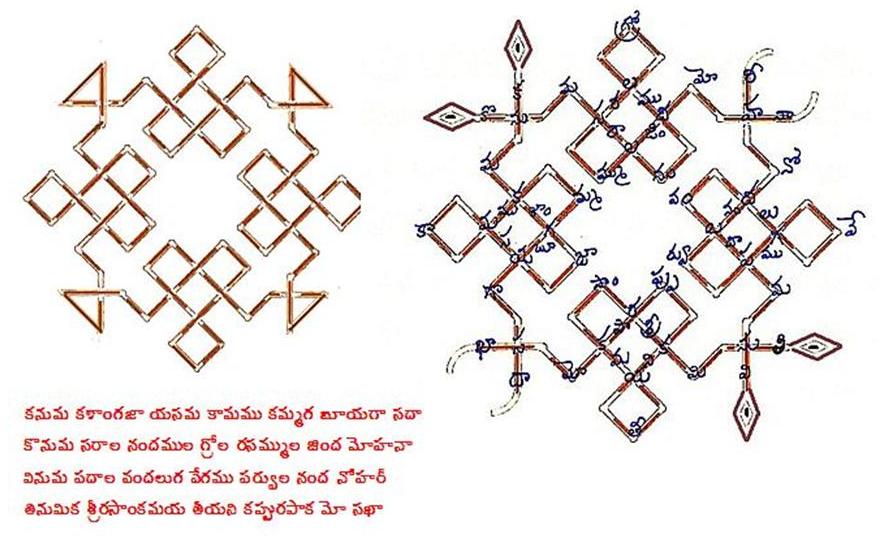
ఇవి చుక్కల ముగ్గులు. చతురస్రముగా చుక్కలను పెడతారు. చుక్కలను వేళ్ళతో ఇసుకపైన పెట్టి వేళ్ళతోనో లేక ఒక కఱ్ఱతోనో ముగ్గును గీస్తారు. దీని విశదీకరణను 1వ చిత్రములో చూడవచ్చును. కొన్ని ముగ్గులకు ఒకే గీత ఉంటుంది, కొన్నిటికి ఒకటికంటే ఎక్కువ గీతలు ఉంటాయి. ఎప్పుడు ఒక గీత ఉంటుందో, ఎప్పుడు ఉండదో అనేది చుక్కలను ఎలా పెడతారో అనే విషయముపైన ఆధారపడి ఉంటుంది. చిన్నవాళ్ళు కూడ చుక్కల అమరికను చూడగానే ఎన్ని గీతలు ఉంటాయో చెప్పగలరట. ఇందులో గణితాంశాలు ఉన్నాయి. అడ్డవరుస సంఖ్య (number of rows), నిడివివరుస సంఖ్య (number of columns) సాపేక్షముగా ప్రధానము లేక అభాజ్యమయితే (relatively prime), అనగా అవి ఏ సంఖ్యతో కూడ విభజించబడకపోతే, మనకు ఒక గీత లభిస్తుంది (ఉదా. 3, 4). వాటి రెంటినీ ఒక సంఖ్యతో విభజించడానికి వీలయితే ఒకటి కన్న ఎక్కువ గీతలు ఉంటాయి (ఉదా. 3, 6 ఈ రెండు అంకెలను 3తో విభజించవచ్చును, దీనికి మూడు గీతలు ఉంటాయి). ఇలాటి ముగ్గును సోనా ముగ్గు అంటారు. 10, 11 కూడ ఇట్టి సంఖ్యలే. వీటితో నేను నిర్మించిన సోనా చిత్రము కథతో సహా ఇంతకుముందే ఈమాటలో చోటు చేసికొన్నది.

4అ. సోనా చతురస్రము

2. సోనా చతురస్రము

ఇంతవరకు సోనా ముగ్గులను గురించి నేను చెప్పిన విషయాలు అందరికీ అవగాహన చేసికొనడానికి అందుబాటులో నున్నవే. ఇట్టి సోనా ముగ్గులను తీసికొని ఇంకా ఏమి చేయడానికి వీలవుతుంది అనేదే తరువాతి నా పరిశోధనలకు అవకాశాన్ని యిచ్చింది. ఈ పరిశోధనల సారాంశాన్ని 2వ చిత్రములో చూడడానికి వీలవుతుంది. ఒకే గీతతో ఉన్న ఒక సోనా ముగ్గును 90 డిగ్రీల చొప్పున తిప్పి ఒకదానితో మరొకదానిని చేరిస్తే మనకు సోనా చతురస్రము లభిస్తుంది. మూడు అడ్డవరుసలు, నాలుగు నిలువు వరుసలతో ఉండే సోనా చతురస్రానికి గల సౌష్ఠవమును పరిశీలిద్దామా?

దీనికి చిత్రతలములో (in the plane of the figure) ఒక దానికొకటి లంబముగా ఉండే రెండు 180డిగ్రీల భ్రమణాక్షములు (mutually perpendicular two-fold axes with 180⁰ rotation) ఉన్నాయి. చిత్రతలానికి లంబముగా మరో 180డిగ్రీల భ్రమణాక్షము ఉన్నది (vertical two-fold axis). రంగుల భేదాన్ని మరచిపోతే దీని సౌష్ఠవము దీనికన్న ఎక్కువ. అప్పుడు దీనికి చిత్రతలానికి లంబముగా 90డిగ్రీల భ్రమణాక్షము (vertical four-fold axis), చిత్రతలములో 45డిగ్రీల చొప్పున నాలుగు 180డిగ్రీల భ్రమణాక్షములు (four two-fold axes) ఉన్నాయి. రంగులతో దీని సౌష్ఠవము తక్కువ, నలుపు-తెలుపుగా దీని సౌష్ఠవము ఎక్కువ. అంచులలో అందాలు అనే నా వ్యాసములో దీనిని గురించి కొద్దిగా చర్చించాను.

3. సోనా సౌష్ఠవము

తరువాత మనము ప్రారంభములో తీసికొన్న సోనాముగ్గును 90 డిగ్రీలు తిప్పితే దానికి అడ్డవరుసలు నాలుగు, నిలువు వరుసలు మూడు ఉంటాయి (four rows and three columns). అట్టి అమరికతో సోనా చతురస్రాన్ని సృష్టించితే 3వ చిత్రము (కుడివైపు, ఎడమవైపు రెండవ చిత్రములోని చివరిది) లభిస్తుంది. దీని సౌష్ఠవము చిత్రతలానికి లంబముగా 90డిగ్రీల భ్రమణాక్షము (vertical four-fold axis), చిత్రతలములో నాలుగు 180డిగ్రీల భ్రమణాక్షాలు (four two-fold axes in the plane of the figure) ఉన్నాయి. అంటే, రంగులు లేకుండా 3 అడ్డ, 4 నిలువు సోనా చిత్రపు సౌష్ఠవము రంగులతో 4 అడ్డ, 3 నిలువు సోనా చతురస్రానికి ఉన్నది. ఇంకా కొన్ని చిత్రాలతో యిట్టి ప్రయోగాలను చేసిన తరువాత దీని వివరణ అర్థమయినది. అదేమంటే –

4ఆ. పరిశోధనల సారాంశము

1. ప్రారంభ సోనా ముగ్గుకు ఒక గీత ఉంటే, సోనా చతురస్రానికి ఎప్పుడూ రెండు గీతలు ఉంటాయి. సుమారు వందకు పైన ముగ్గులతో చేసిన ప్రయోగాలవలన తేలిన సారాంశ మిది. గణితశాస్త్రరీత్యా దీనిని ఇంకా నిరూపించలేదు.
2. నిలువు వరుసల సంఖ్య బేసిగా (odd number of columns) ఉంటే, సోనా చతురస్రానికి సౌష్ఠవము ఎక్కువగా ఉంటుంది (చిత్రతలములో నాలుగు 180 డిగ్రీల భ్రమణాక్షాలు, లంబముగా 90 డిగ్రీల భ్రమణాక్షము, దీనినే శాస్త్రీయముగా 422 అంటారు).

3. 
   4. దారముతో అల్లిన సోనా సౌష్ఠవము

   నిలువు వరుసల సంఖ్య సరి సంఖ్య అయితే (even number of columns), సోనా చతురస్రానికి సౌష్ఠవము తక్కువ (చిత్రతలములో రెండు 180 డిగ్రీల భ్రమణాక్షములు, చిత్రానికి లంబముగా 180 డిగ్రీల భ్రమణాక్షము. దీనినే శాస్త్రీయముగా 222 (three mutually perpendicular two-fold axes) అంటారు.

4. ప్రారంభ ఏకరేఖా సోనాచిత్రాలకూ (starting single line motifs), సోనా చతురస్రాలకు సవ్యాపసవ్య గుణము ఉన్నది (chirality). అంటే యీ ముగ్గులకు బింబప్రతిబింబ ధర్మము ఉన్నది.

5. సోనా మూషికము

ఇట్టి సోనా చతురస్రాలను దారాలతో, తాడులతో నిర్మించవచ్చును. నైలాను దారాలతో నిర్మించిన అట్టి ఒక నా ప్రయత్నాన్ని 4వ చిత్రములో చూడగలరు. ఏకరేఖా సోనా చిత్రాలతో ఇంకా ఎన్నో గమ్మత్తులను చేయవచ్చును. ఒక జంతువు లేక మనిషి ఇత్యాదుల ఆకారములో ఒక సరియైన సోనా చిత్రాన్ని నిర్మించి వాటిని పొడిగిస్తే మనకు ఆ ఆకారము ఏకారేఖా చిత్రముగా పరిణామమవుతుంది. వినాయకుడికి ప్రియమైన మూషికపు ఏక రేఖా చిత్రాన్ని 5వ చిత్రములో చూడవచ్చును.

4ఇ. విరహాంక-హేమచంద్ర-ఫిబనాచ్చి సంఖ్యాశ్రేణి

ఏడవ శతాబ్దములో విరహాంకుడు అనే ఒక ఛందశ్శాస్త్రజ్ఞుడు జీవించాడు. మాత్రావృత్తాలను వివరించేటప్పుడు అతడు ఒక సంఖ్యాశ్రేణిని విశదీకరించాడు. దాని సారాంశ మేమంటే ఒక మాత్రను ఒక విధముగా (I), రెండు మాత్రలను (I – లఘువు -ఒక మాత్ర, U – గురువు, రెండు మాత్రలు) రెండు విధములుగా (U, II), మూడు మాత్రలను మూడు విధములుగా (III, UI, IU), నాలుగు మాత్రలను ఐదు విధములుగా (IIII, IIU, IUI, UII, UU), ఐదు మాత్రలను ఎనిమిది విధములుగా (UUI, UIU, IUU, UIII, IIIU, IUII, IIUI, IIIII), ఇలాగే మిగిలినవి వ్రాయవచ్చును. 1,1,2,3,5,8,13,… దీనిని మాత్రామేరు ప్రస్తారము అంటారు. ఇలాటివి సంగీతములోని తాళాలలో కూడా ఉన్నాయి. తరువాత హేమచంద్రుడు కూడ ఛందోనుశాసనములో ఈ సంఖ్యలను ప్రస్తావించాడు. ఆ తరువాత పశ్చిమ దేశాలలో నేడు ఈ సంఖ్యాశ్రేణిని ఫిబనాచ్చి సీరీస్ (Fibonacci series) అంటారు. దీనిని గురించి మరొకప్పుడు ప్రత్యేక వ్యాసమును వ్రాస్తాను.

6. విరహాంక సౌష్ఠవము

ఈ శ్రేణి ఎక్కడెక్కడ ప్రకృతిలో పెరుగుదల (growth) సంభవిస్తుందో అక్కడ కనిపిస్తుంది. అందుకే దీనిని dynamic symmetry అంటారు. దీనిని ఫిబనాచ్చి (Fibonacci) కంటె మూడు శతాబ్దాలకు ముందు కనుగొన్న విరహాంకునికి గణితశాస్త్రములో పేరు, గౌరవము లభించకుండుట శోచనీయము. ఈ అంకెలతో సోనా ముగ్గులను నిర్మించినప్పుడు నేను ఒక కొత్త విషయాన్ని గమనించాను. a, b, c, d లు నాలుగు విరహాంక సంఖ్యలైతే, c, dలను అడ్డ, నిలువు వరుసలుగా ఒక ఏకరేఖా సోనాచిత్రాన్ని సృష్టిస్తే అందులో మరో మూడు సోనా ముగ్గులు ఉంటాయి. వాటి అడ్డ నిలువు వరుసలు [b, c], [c, b], [a, c]. a+b=c, b+c=d అయితే cd = bc + cb + ac అవుతుంది. ఇట్లు నిర్మించిన విరహాంకసంఖ్యా చిత్రాలలో ఒక దానిని యిక్కడ 6వ చిత్రములో (పైభాగములో 8 అడ్డవరుసల, 13 నిలువు వరుసల సోనా ముగ్గు; క్రింది భాగములో అదే చిత్రములో 5×8, 8×5, 3×8 వరుసల మూడు సోనా ముగ్గులు) చూడ వచ్చును. ఈ ఏకరేఖాచిత్రాలతో సోనా చతురస్రాన్ని నిర్మిస్తే, దానికి రెండు రంగుల గీతలు ఉంటాయి.

4ఈ. శ్రీవత్స చిహ్నము

సోనా ముగ్గులను ముగించే ముందు బౌద్ధులకు పూజార్హమైన పవిత్రమైన అష్ట చిహ్నాలలో ఒకటైన శ్రీవత్స అనే ఒక చిహ్నాన్ని గురించి యిక్కడ చెప్పాలి. రెండు అడ్డ వరుసలు, మూడు నిలువ వరుసల చుక్కలతో ఒక గీతతో ఉండే సోనా ముగ్గుకు అదనముగా పైన, కింద మరో చుక్క పెట్టితే మనకు శ్రీవత్స చిహ్నము లభిస్తుంది. టిబెట్ బౌద్ధమతములో నేడు కూడ లాసాలోని ఆలయాలలో దీనిని పతాకాలుగా వేలాడదీస్తారు. దీనినే అంతులేని ముడి (eternal knot) అంటారు. పునరపి జననం పునరపి మరణం పునరపి జననీ జఠరే శయనం అనే సూక్తిని ఈ శ్రీవత్స చిహ్నము తెలుపుతుంది. విష్ణువు వక్షఃస్థలముపై వెండ్రుకలు యీ శ్రీవత్సాకారములో ఉంటాయని కూడా అంటారు. సోనా సౌష్ఠవముతో ఇలా ఎన్నో కొత్త కొత్త ముగ్గులను సృష్టించాను, కాని వ్యాసపు నిడివి పెరుగుతుందని ఆ విషయాలను యిక్కడ చర్చించడంలేదు.

5. మెర్సాన్ సంఖ్యలతో ముగ్గులు

7. మెర్సాన్ ముగ్గు

గణితశాస్త్రములో మెర్సాన్ సంఖ్యలు (Mersenne numbers) ప్రసిద్ధమైనవి. వీటిని 2ⁿ – 1 where n is 1, 2, 3,… అనే ఫార్ములాతో గుర్తించవచ్చును. ఈ సంఖ్యలు గల చుక్కలతో ముగ్గులను వేయ వీలవుతుంది. ఆ విధానాన్ని 7వ చిత్రములో తెలిపినాను.

8. ఏడు చుక్కల మెర్సాన్ ముగ్గు

ఒక చిన్న చతురస్రానికి నాలుగు వైపుల నాలుగు చిన్న చతురస్రాన్ని (చిత్రము a) చేర్చితే మనకు (b) చిత్రము లభిస్తుంది. ఐదు (b) చిత్రాలను ఒకటిపైన మరొకటి ఉంచితే (c) చిత్రము లభిస్తుంది. దీనికి ఏడు చుక్కలు. ఇలాగే 15 చుక్కలు ఉండే (d) చిత్రము, 31 చుక్కలు ఉండే (e) చిత్రాలను సృష్టించవచ్చును. వీటిని చూస్తే మనకు fractal patterns జ్ఞాపకము వస్తుంది. వీటికి ఒకే గీత ఉంటుంది. ఏడు చుక్కలు ఉండే ఈ మెర్సాన్ ముగ్గును 8వ చిత్రములో చూడవచ్చును.

6. నక్షత్రాకార బహుభుజి

శాస్త్రీయ సిద్ధాంతాలపైన ఆధారపడిన మరి కొన్ని ముగ్గులు నక్షత్రాకార బహుభుజికి (Star Polygon) చెందినవి. ఉదాహరణకు ఒక అష్టభుజాన్ని తీసికొందాము (చిత్రము 9a). పక్కపక్కన ఉండే కొనలు (అగ్రాలు) కలుపబడ్డాయి యిందులో. దీనికి ష్లాఫ్లీ చిహ్నము (Schläfli symbol) ‘8/1’. చిత్రము 9b లో ఇదే అష్టభుజిని రెండు రెండు అగ్రాలకు కలుపగా వచ్చిన ఆకారము చూపబడినది. ఈ ఆకృతి రెండు గీతలతో నక్షత్రాకారములో ఉన్నది. దీని ష్లాఫ్లీ చిహ్నము ‘8/2’. చిత్రము 9c లో మూడు మూడు కొనలు కలుపబడ్డాయి, అలా చేస్తే ఒకే గీతతో ఒక నక్షత్రాకారము వచ్చినది. ఇది అందరికీ పరిచితమైన ముగ్గు.

9. బహుభుజి ముగ్గు

ఇట్టి ముగ్గును మాతృకగా తీసికొని ఒక బంధకవిత్వమును కూడ నేను కౌముదిలో ప్రచురించిన ముగ్గులపై వ్యాసములో వ్రాసినాను. చిత్రము 9d, 9e, 9f లలో హృదయాకారములో ఉండే ఒక అసంపూర్ణ దీర్ఘవృత్తము (incomplete ellipse) 8/1, 8/2, 8/3 నక్షత్రాకృతులకు సరిపోయే కోణాలతో నిర్మించబడినవి. వీటిని ఒక విధమైన హృదయకమలాలు అని చెప్పవచ్చును. చిత్రము 9g లో చిత్రము 9b వలె చెక్కబడిన హంపీలోని ఒక స్తంభముపైన ఉండే శిల్పాన్ని చూపాను. చిత్రము 9h లో చిత్రము 9f వలె నైలాను దారముతో నేను అల్లిన ఒక అమరికను చూపాను. ఇలాగే పంచభుజికి (5/1) 5/2 నక్షత్రము, షడ్భుజికి (6/1) రెండు గీతలతో 6/2 Star of David, సప్తభుజికి (7/1) 7/2, 7/3 ఆకృతులు లభిస్తాయి.

7. ముడుల సిద్ధాంతము

10. ముడి సంఖ్యల ముగ్గు

మెలిక ముగ్గులలోని ముడులు ముడుల సిద్ధాంతమును (knot theory) అనుసరిస్తాయి. ముగ్గులో రెండు గీతలు ఎక్కడ ఒకదాని కింద మరొకటి పోతుందో, ఆ బిందువును సంధి స్థానము (crossover point) అంటాము. నేను ముందు వివరించిన సోనా ముగ్గులో, r అడ్డ వరుసలు, c నిలువు వరుసలు ఉంటే, దానికి (r-1) (c-1) – 1 సంధి స్థానములు ఉంటాయి. ఉదాహరణకు, 6 అడ్డ వరుసలు, 5 నిలువు వరుసలు ఉంటే, మనకు 19 సంధిస్థానాలు ఉంటాయి. ప్రతి సంధి స్థానపు సంఖ్యకు ఎన్నో చిత్రాలను మనము వ్రాయవచ్చును. మూడు, నాలుగు సంధి స్థానాలకు ఒక చిత్రము, ఐదు సంధి స్థానాలకు 2 చిత్రాలు, ఆరింటికి మూడు, ఏడింటికి ఏడు, ఎనిమిదికి 21, తొమ్మిదికి 49, ఇలా పెరుగుతూ పోతుంది ఈ సంఖ్య. అదీకాక, గీత (లేక దారము) ఎప్పుడూ వంకర లేకుండా ఉండాలని లేదు. అలా వంకరటింకర గీతలతో ఒక ప్రత్యేకమైన ముడి సంఖ్యతో మనము మన ఊహకు తోచినట్లు చిత్రాలను సృష్టించవచ్చును. అలా సృష్టించిన ఒక చిత్రాన్ని 10వ చిత్రములో చూడవచ్చును.

8. నాగబంధము

మెలిక ముగ్గులలో ముఖ్యమైన ఒక ముగ్గు నాగమండలము. దీనినే నాగబంధము అని కూడ అంటారు. తమిళనాడులో కావేరీ నదీతీరములో కరూరు పట్టణములో పశుపతీశ్వరుని గుడి ఒకటి ఉన్నది. ఇది సుమారు పదవ శతాబ్దపు కాలము నాటిది. ఈ ఆలయస్తంభాలపైన కొన్ని అపురూపమైన నాగమండలాలు ఉన్నాయి. పదమూడవ శతాబ్దపు ఉత్తరార్ధములో హోయసల రాజులు మైసూరు సమీపములో సోమనాథపుర దేవాలయాన్ని నిర్మించారు. ఈ ఆలయపు పైకప్పులో నాగమండలము(5వ చిత్రము) ఒకటి వుంది. తిరుక్కడైయూరు అమృతఘటేశ్వరాలయములో కూడ ఒక సర్పబంధ శిలాఫలకము గలదు.

11. ఇరట్టై నాగబందం

చిత్రకవితలో ఒక భాగము బంధకవిత్వము, ఈ బంధకవిత్వములో వివిధ ఆకారాలకు సరిపోయేటట్లు అక్షరాలను ఉంచి పద్యాలు వ్రాస్తారు. ఇది పద్యముతో crossword puzzle లాటిది. తొలి బంధకవిత్వాలు (చక్రబంధము, గోమూత్రికాబంధము, మురజబంధము మున్నగునవి) మాఘుని శిశుపాలవధలో, భారవి కిరాతార్జునీయములో, కుమారదాసుని జానకీహరణములో ఉన్నాయి. గోమూత్రికాదులను ఏడవ శతాబ్దపు దండి తన కావ్యాదర్శము^[6]లో ఉదహరించాడు. కాని అందులో నాగబంధము లేదు. ఈ దండి కావ్యాదర్శానికి తండి యలంగారం^[7] అని ఒక తమిళ అనువాదము వుంది. అందులో ఇరట్టై నాగబందం (రెండు పాములతో బంధము)అని ఒక నాగబంధము ఉన్నది.

12. కుమారసంభవ నాగబంధం

దండి దక్షిణ దేశస్థుడైనా (కాంచీపుర నివాసి అంటారు), ఈ తండి యలంగారం దండి వ్రాసినది కాదు, దండి అలంకారానికి అనువాదము కాబట్టి దీనికి తండియలంగారం అని పేరు వచ్చిందని తమిళ ఛందస్సు నెరిగిన పొన్ పశుపతి తెలిపారు. ఏది ఏమైనా, సంస్కృతములో మొట్ట మొదట కుండలినీ నాగబంధము కృష్ణకవి మందారమరంద చంపువులో కనబడుతుంది. ఈ కృష్ణకవి క్రీ.శ. 1650 కాలము నాటివాడు అంటారు^[8].

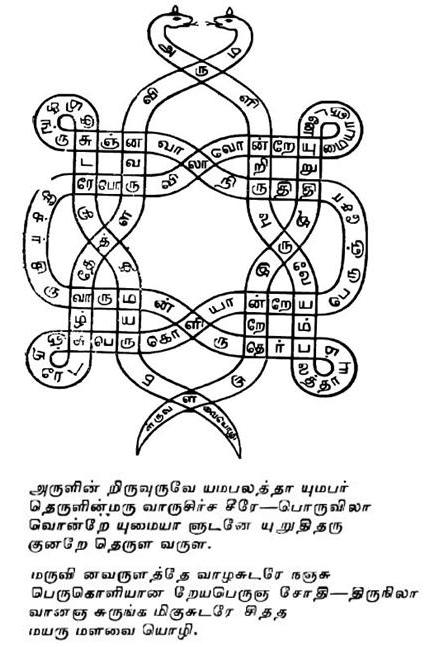
కన్నడములోని కవిరాజమార్గములో కూడ నాగబంధము లేదు. కాని తెలుగులో నన్నెచోడుని కుమారసంభవములో ఒక నాగబంధము ఉన్నది. ఆ పద్యాన్ని 12వ చిత్రములో చూడగలరు. నన్నెచోడుడు బహుశా నన్నయకు సమకాలికుడని యింతకు ముందే నేను చర్చించాను.

13. ఏకరేఖా నాగబంధం

నన్నెచోడునికి ఈ తండి యలంగారపు నాగబంధ చిత్రాలు పరిచితములై ఉండవచ్చును. దానిని, దక్షిణ దేవాలయాల స్తంభలను చూచి యితడు తన నాగబంధాన్ని కల్పించి ఉంటాడని నా ఊహ. ఎఱ్ఱ నైలాను తాడుతో చేసిన నాగబంధ ఏకరేఖ చిత్రాన్ని 13వ చిత్రములో చూడ వీలగును. దీనిని కత్తిరించి తలను, తోకను పెట్టితే అది నాగబంధపు చిత్రము అవుతుంది. సంస్కృతములో నాగబంధాన్ని 21 అక్షరాల స్రగ్ధరావృత్తములో వ్రాస్తారు, తెలుగులో సామాన్యముగా అదే 21 అక్షరాల చంపకమాలలో వ్రాస్తారు దీనిని ఇతర వృత్తాలలో కూడ వ్రాయవచ్చును. నేను ఈ మధ్య వ్రాసిన ఒక కొత్త విధమైన నాగబంధ కవిత ప్రార్థనా చిత్రాన్ని 14వ చిత్రములో చూపుతున్నాను.

9. ముగింపు

సుమారు వంద సంవత్సరాలకు ముందు సామాన్యముగా కులీనుల యిండ్ల స్త్రీలకు కూడ చదువు రాదు. చరిత్రలో ఆతుకూరి మొల్లలు, అవ్వయ్యారులు అరుదు. సామాన్య స్త్రీ పని వంటిల్లు, పిల్లల పెంపకము, పూజలు పునస్కారాలు, పండుగలు పబ్బాలు, యిత్యాదులే. చదువు లేకపోయినా మిగిలిన లలితకళలలో కూడ నాట్యము వారు చేయకూడదు. సానులు తప్ప సంసారుల యిళ్ళల్లో ఆడపడుచులు నాట్యమాడరు. ఇక మిగిలిందల్లా పూజ పాటలు, పెళ్ళి పాటలు, లాలి పాటలు పాడడము, దేవతాగృహములో, యింటి ముంగిలిలో, అరుగులపైన ముగ్గులు వేయడము. కాని యీ రెండు లలితకళలలో వారు ఎంతో ప్రావీణ్యతను గడించారు. తరతరాలుగా స్త్రీలు పాడిన పాటలు కొన్ని మరుగుబడిపోయినా, మరి కొన్ని యింకా చెలామణిలో ఉన్నాయి.

14. నాగబంధ కవితా ప్రార్థన

ముగ్గులు స్త్రీల సొత్తు, నాటికీ నేటికీ కూడ. ఆ కాలములోని కవయిత్రుల వలెనే ఈ కాలములోని పురుష రంగవల్లి కళాకారుల సంఖ్య తక్కువే. సుప్రసిద్ధ కళాకారుడు మనోహర్ దేవదాస్ Greenwell Years^[9] అనే పుస్తకములో ముగ్గులపైన ఆసక్తి చూపే ఒక కుఱ్ఱవాడిని మిగిలిన వాళ్ళు పొట్టయ్యన్ అని ఎగతాళి చేసేవారని రాశాడు. ఈ పొట్టయ్యన్ పదము మన ఆడంగి వంటిది. మిగిలిన దేశాలలో మగవాళ్ళు ముగ్గులవంటి కళలలో ప్రవీణులైనా, మన భారతదేశములో యిప్పుడు కూడ యిది ఆడవాళ్ళ సొత్తే. ముగ్గులు వేయడానికి నేర్పు మాత్రమే కదు, ఓర్పు కూడ కావాలి. ముగ్గులు పెట్టడము నా ఉద్దేశములో ఒక తెరపీ (therapy) లాటిది. మనస్సుకు శాంతిని యిస్తుంది, మెదడుకు ఏకాగ్రతను యిస్తుంది. నేను ఎరిగి ఉన్నవారిలో కొందరు ఉదయము నాలుగున్నరకు లేచి గంట, గంటన్నర ముగ్గులు పెడతారు. మంచి ముగ్గులను వేసి సంతోషించడము మాత్రమే కాదు, దానిని తుడిచేటప్పుడు కష్టమవుతుంది. కాని పాత ముగ్గు ఉన్నచోట మరొక కొత్త ముగ్గు సృష్టించబడుతుంది. కాలచక్రములో దైనందినము జరిగే మార్పులలో యిదొకటి.

10. ముగ్గుపై కవితలు

ఒక రెండు కవితలతో ఈ వ్యాసాన్ని ముగిస్తాను. మొదటిది ముగ్గుపొడి పైన, రెండవది (మత్తకోకిల ద్విపద) ఎన్ని విధాలైన ముగ్గులున్నా అవన్నీ ఆ సర్వేశ్వరునికి సమర్పించే ప్రార్థనాచిత్రాలే.

1. ముగ్గుపొడీ, నువ్వొక పిడికెడు తెల్లటి పొడివి
   నా తలపైన ఉండే ముగ్గుబుట్టకు తోడు నువ్వు
   ఇంతలో ఆమె నిన్ను తన చేతిలో తీసికొంటుంది
   మెల్లగా తన వ్రేళ్ళ ద్వారా నిన్ను రాలుస్తుంది
   నువ్వు ఆశతో నిరీక్షించే చుక్కలయ్యావు
   నువ్వు గీత లయ్యావు, వంపు లయ్యావు, గుండ్రటి వృత్తాలయ్యవు
   నువ్వు భావా లయ్యావు, రూపా లయ్యావు, చిత్ర లయ్యావు
   నువ్వు పువ్వు లయ్యావు, భ్రమరా లయ్యావు
   నువ్వు నెమ ళ్ళయ్యావు, పాము లయ్యావు
   నువ్వు కల లయ్యావు, ఆనందపు టల లయ్యావు,
   నువ్వు ఆట లయ్యావు, పాట లయ్యావు
   నువ్వు నవ్వు లయ్యావు, దివ్వె లయ్యావు
   నువ్వు చైతన్య మయ్యావు, నువ్వు జీవంత మయ్యావు
   వాడి చేతిలోని వెదురు పిల్లనగ్రోవి అయింది
   ఆమె చేతిలో నువ్వు ప్రార్థనాచిత్రమై
   స్వర్గానికే నిచ్చెన వేశావు
2. చిన్న ముగ్గులు పెద్ద ముగ్గులు చిక్కు ముగ్గులు చూడ రా
   సన్న ముగ్గులు మెలిక ముగ్గులు సంజ ముగ్గులు నీకెరా

   వన్నె ముగ్గులు పూల ముగ్గులు పాము ముగ్గులు గాంచ రా
   కన్నె ముగ్గులు రవల ముగ్గులు కావి ముగ్గులు నీకెరా

   పూస ముగ్గులు పొడుల ముగ్గులు పూజ ముగ్గులు కనగ రా
   కాసు ముగ్గులు గింజ ముగ్గులు గవ్వ ముగ్గులు నీకెరా

   పిండి ముగ్గులు నిడివి ముగ్గులు పీట ముగ్గులు వేడ్కరా
   పెండ్లి ముగ్గులు రంగు ముగ్గులు ప్రేమ ముగ్గులు నీకెరా

   తట్ట ముగ్గులు సుద్ద ముగ్గులు తమ్మి ముగ్గులు సొంపురా
   మట్టి ముగ్గులు పట్టె ముగ్గులు మణుల ముగ్గులు నీకెరా

   పసుపు ముగ్గులు తీగ ముగ్గులు పలక ముగ్గులు చెలువురా
   యిసుక ముగ్గులు తాడు ముగ్గులు యెఱుపు ముగ్గులు నీకెరా

   నవత ముగ్గులు రేకు ముగ్గులు నగల ముగ్గులు భళిభళీ
   కవిత ముగ్గులు ఆకు ముగ్గులు కమ్మి ముగ్గులు నీకెరా

గ్రంథసూచి

1. క్రీడాభిరామము, వినుకొండ వల్లభరాయడు, ఎమెస్కో బుక్స్, విజయవాడ, 1997.
2. ఆంధ్రుల సాంఘిక చరిత్ర, సురవరము ప్రతాపరెడ్డి, ఆంధ్ర సాహిత్య పరిషత్తు, హైదరాబాదు, 1950.
3. ఆముక్త మాల్యద, శ్రీకృష్ణదేవరాయలు, తెలుగు విశ్వవిద్యాలయము, హైదరాబాదు, 1995.
4. విజయవిలాసము, చేమకూర వేంకటకవి, తెలుగు విశ్వవిద్యాలయము, హైదరాబాదు, 1995.
5. శ్రీవర్ణనరత్నాకరము, 1,2, దాసరి లక్ష్మణస్వామి, శ్రీ విద్వజ్జన మనోరంజనీ ముద్రాక్షరశాల, పిఠాపురము, 1928; శ్రీవర్ణనరత్నాకరము, 3,4, దాసరి లక్ష్మణస్వామి, శ్రీ విద్వజ్జన మనోరంజనీ ముద్రాక్షరశాల, పిఠాపురము, 1930.
6. కావ్యాదర్శః, దండి, వ్యాఖ్య పుల్లెల రామచంద్రుడు, ఆంధ్రప్రదేశ్ సాహిత్య అకాడమీ, హైదరాబాదు, 1981.
7. తండి యలంగారం, సుబ్రమణ్య దేశికర్ వ్యాఖ్య, తిరునెల్వేలి తెన్నిందియ శైవ శిత్తాంద నూర్పదిప్పు కళగం, తిరునెల్వేలి, 1943.
8. చిత్రం – చిత్రబంధ, V. బాలసుబ్రమణ్యం, రాష్ట్రీయ సంస్కృత సంస్థానం, న్యూ ఢిల్లీ, 2010.
9. Green Well Years, Manohar Devadoss, East-West Books, Madras, 1997.