ఇది నోబెల్ బహుమతుల సమయం. మన చుట్టూ ఉన్న అజ్ఞానపు చీకటిని కొంతైనా తొలగించడానికి జ్ఞాన దీపాలని వెలిగించిన మహామేధావులని సన్మానించే సమయం. ఈ సందర్భంలో కొడవటిగంటి కుటుంబరావు మాటలు గుర్తుకొస్తున్నాయి: “జ్ఞానం ప్రసాదించే జ్ఞానజ్యోతిలో విశేషమేమంటే, ఎక్కడికక్కడ దాని ప్రకాశం పరిమితంగా ఉంటుంది. … ఎప్పటికప్పుడు కొత్త శాస్త్ర జ్ఞానం లభిస్తూంటే తప్ప మానవుడికి ఐహిక, సాంఘిక పురోగమనం ఉండదు. అందుచేత ఎప్పటికప్పుడొక కొత్త జ్ఞానజ్యోతిని వెలిగించిన వారు మహాపురుషుల వంటి వారు. పరిణామవాదానికి రూపం ఇచ్చిన డార్విన్, సాపేక్ష సిద్ధాంతాన్ని ప్రతిపాదించిన ఐన్‌స్టయిన్ లాంటి శాస్త్రవేత్తలు మహాపురుషులు.”

ఆ కోవకి చెందిన వాడే బ్రిటిష్ గణితవేత్త ఆలన్ ట్యూరింగ్ (Alan Mathison Turing, 23 జూన్ 1912 – 7 జూన్ 1954.)

ఆలన్ ట్యూరింగ్ (1912 – 1954)

మీ జేబులోని ఫోనులో ఓ చిన్న కంప్యూటర్ ఉంది. మీ ఒళ్ళోని ల్యాప్‌టాప్లో అంతకన్నా వేగంగా పనిచేసే కంప్యూటర్ ఉంది. ప్రభుత్వ పరిశోధనా సంస్థల్లోనూ, ప్రైవేటు కంపెనీలలోనూ దాని కన్నా అనేక రెట్లు వేగంగా పనిచేసే కంప్యూటర్లు ఉన్నాయి. కాని ఆ పెద్ద పెద్ద కంప్యూటర్లు చెయ్యగల పని దేనినయినా సరే మీ జేబులోని కంప్యూటర్ కూడా చెయ్యగలదు. ఒక కంప్యూటర్ చేసే పని ఏదైనా మరో కంప్యూటర్ చెయ్యగలదు. ఒకటి తొందరగా చేస్తే మరొకటి నింపాదిగా చెయ్యవచ్చు గాని, ఫలితంలో మార్పు ఉండదు.

అంతకన్నా చిత్రమైన విషయం, ఆ కంప్యూటర్లు చేసేదేదైనా సరే ఓ కాగితపు టేపు మీద గడులపై పెన్సిలుతో కదుల్తూ రాసే యంత్రం చెయ్యగలదు. అంతే కాదు, ఆ పేపరు-పెన్సిలు యంత్రం చెయ్యలేనిది మరే కంప్యూటర్లూ – ఇప్పుడున్నవే కాక భవిష్యత్తులో ఇంజనీర్లు కనుక్కునేవి కూడా – చెయ్యలేవు. ఒక్కసారి ఆగి ఆ వాక్యంలోని లోతైన భావాన్ని గ్రహించండి. మనం కంప్యూట్ చెయ్యగలిగే వాటికి హద్దులున్నాయి – మినహాయింపులు లేని హద్దులు. ఆ హద్దులూ ఈ పేపరు-పెన్సిలు యంత్రం హద్దులూ ఒకటే.

అది వాస్తవమైన యంత్రం కూడా కాదు. కేవలం ఓ భావన. గణిత పునాదులపై డేవిడ్ హిల్బర్ట్ వేసిన ఓ సవాలుని సాధించే యత్నంలో ఆలన్ ట్యూరింగ్ తలవని తలంపుగా ఆధునిక కంప్యూటర్‌కి 1936లో అంకురం వేశాడు. అలా అతను వెలిగించిన గోరంత దీపం ఇవాళ ప్రపంచంలో నలుమూలలా కొండంత వెలుగు నిస్తుందనడంలో అతిశయోక్తి లేదు. కాని అతని పని, జీవితం గురించి మన దేశంలో చదువుకున్నవాళ్ళలో కూడా చాలామందికి తెలిసింది బహు తక్కువనే చెప్పాలి.

కంప్యూటర్ సైన్సులో నోబెల్ బహుమతి లేదు కాని ట్యూరింగ్ పేరు మీద దానికి దీటైన బహుమతి వుంది. దాదాపు గత యాభై ఏళ్ళుగా ప్రతి సంవత్సరం దీనిని కంప్యూటర్ సైన్సులో చెప్పుకోదగ్గ పరిశోధనలని చేసిన వారికి ఇస్తున్నారు. మన దేశస్థులలో కంప్యూటర్ ఇంజనీర్లు అనేక లక్షల మంది ఉన్నా ఇంతవరకు ఇది మనకి ఒకే ఒక్కసారి దక్కిందంటే కొంత విచారం కలగచ్చు. కాని అది మన తెలుగువాడికని కాస్త గర్వపడొచ్చు. కార్నెగీ మెలన్ విశ్వవిద్యాలయంలో రొబోటిక్స్ ప్రొఫెసరు దబ్బల రాజగోపాల్ రెడ్డి (Raj Reddy) కృత్రిమమేధారంగంలో (Artificial Intelligence) చేసిన పరిశోధనలకి 1986 అవార్డుని స్టాన్‌ఫర్డ్ విశ్వవిద్యాలయం ప్రొఫెసర్ ఫైగెన్‌బామ్‌తో (Edward Feigenbaum) పంచుకున్నారు.

ట్యూరింగ్ జీవితం విస్మయ విషాదాలతో కూడుకున్నది. చాలా మంది కంప్యూటర్ సైన్సు చదివిన వాళ్ళకి కూడ తెలియని విషయం ఒకటి చెప్పనా? అసలు ఈ ట్యూరింగ్ వాళ్ళమ్మ కడుపున పడింది మన తెలుగుదేశపు సరిహద్దుల్లోనే. ఎవరో కొందరు గణితవేత్తలకి మాత్రమే పట్టే పరిశోధనకి పరిమితమైన వాడు కాదు. రెండవ ప్రపంచ యుద్ధంలో శత్రుసేనలని ఓడించడంలో ట్యూరింగ్ కీలక పాత్ర వహించాడు. జర్మన్ సైన్యాల రహస్య సందేశాలని విడగొట్టే యుక్తులు కనిపెట్టాడు. వాటితో బ్రిటిష్ సైన్యం నాజీ జర్మన్లు చెయ్యబోయే దాడులని ముందే పసిగట్టి, వాళ్ళ నావలని సముద్రంలో కూల్చి విజయం సాధించగలిగింది. అందుకు బ్రిటిష్ ప్రభుత్వం ట్యూరింగ్‌కి అత్యున్నత పురస్కారం (Order of the British Empire) ఇచ్చి గౌరవించింది. యుద్ధం తర్వాత ఆ ప్రభుత్వమే, అతని స్వలింగసంపర్క ప్రవర్తనని అప్పట్లో అమలులో ఉన్న చట్ట నిబంధనల ప్రకారం ‘తీవ్రమైన అసభ్యతా నేరం’గా (gross indecency) పరిగణించి కోర్టు కేసు పెట్టింది. ట్యూరింగ్ క్షమాపణ చెప్పడానికి నిరాకరించాడు. జడ్జి కొంత మానవీయ దృష్టితో జైలు శిక్ష వెయ్యకుండా, లైంగిక కోరికలు తగ్గించే హార్మోనుల చికిత్స విధించాడు. కొన్నాళ్ళు వాడి మందులనిక భరించలేక ట్యూరింగ్ సైనైడ్‌లో ముంచిన యాపిల్ ముక్క తిని ఆత్మహత్య చేసుకున్నాడు. అప్పటికతని వయసు 41 సంవత్సరాలు మాత్రమే. దాదాపు అరవై ఏళ్ళ తర్వాత, 2013లో ట్యూరింగ్ శతజయంతి సందర్భంగా, ట్యూరింగ్ చేసిన పనులు ఆధునిక కంప్యూటర్ యుగంపై అతని ప్రభావం ప్రపంచ వ్యాప్తంగా తెలియ వచ్చింతర్వాత, బ్రిటిష్ ప్రభుత్వం క్షమాపణ చెప్పుకుంది.

ట్యూరింగ్ బాల్యం

అవి మన దేశాన్ని బ్రిటిష్ వాళ్ళు పాలించే రోజులు. ఇంగ్లాండులో జూలియస్ ట్యూరింగ్ ప్రతిష్ఠాత్మకమైన ఇండియన్ సివిల్ సర్వీస్ పరీక్షలో మంచి ర్యాంకుతో పాసయ్యాడు. బ్రిటిష్ పాలనా పద్ధతులూ మన దేశ చరిత్రా చదువుకున్నాడు. తమిళ భాషని నేర్చుకున్నాడు. 1896లో మద్రాసు ప్రెసిడెన్సీకి డిప్యూటీ కలెక్టరుగా ఉద్యోగం వచ్చింది. పదేళ్ళు బెళ్ళారి, కర్నూలు, విజయనగరం మొదలైన జిల్లాలలో పల్లెటూళ్ళని విస్తృతంగా పర్యవేక్షించాడు. వ్యవసాయం, నీటివసతి, పారిశుద్ధ్యం, ఆరోగ్యం, వీటన్నిటి మీదా నివేదికలు రాశాడు. తెలుగు భాషని కూడా నేర్చుకున్నాడు.

మన దేశం నుండి అమెరికా చదువుకోడానికి వచ్చిన అబ్బాయిలు, ఉద్యోగం రాగానే తిరిగి వెళ్ళి అమ్మాయిని చూసి పెళ్ళి చేసుకురావడం ఈ మధ్య దాకా ఆనవాయితీ. అప్పట్లో మన దేశంలో ఉన్న బ్రిటిష్ యువకుల పద్ధతి కూడా అదే. పదేళ్ళ తర్వాత పెళ్ళి చేసుకోడానికి జూలియస్ తన దేశం ప్రయాణమయ్యాడు. ఓడలో ఈథెల్ సేరాతో పరిచయమయింది. ఈథెల్ తండ్రి ఎడ్వర్డ్ స్టోనీ (Edward Stoney) మన దేశంలో రైల్వేలకు (Madras and Southern Mahratta Railway) ఛీఫ్ ఇంజనీరుగా పనిచేశాడు. అనేక నదుల మీద కట్టిన బ్రిడ్జులలో, ముఖ్యంగా తుంగభద్ర బ్రిడ్జి కట్టడంలో కీలక పాత్ర వహించాడు. రైళ్ళకి సంబంధించి చాలా పేటెంట్లు పొందాడు – వాటన్నిట్లోకీ నిద్రాభంగం కలగకుండా గాలి వీచే చక్రం (Stoney’s silent Punkah-wheel) మీద పేటెంట్ ఆంగ్లో-ఇండియన్లకి నచ్చింది. ఈథెల్ పుట్టింది మద్రాసు దగ్గర పొదనూరులో, పెరిగింది ఐర్లాండులో. ఆరేడేళ్ళు మన దేశంలో ఉండి తను కూడా పెళ్ళి చేసుకోడానికి తన దేశం ప్రయాణమయింది.

ఓడ తీరాన్ని చేరేటప్పటికి ఇద్దరి మనసులు కలిశాయి. డబ్లిన్‌లో పెళ్ళి చేసుకొని మన దేశానికి తిరిగొచ్చారు. కూనూరులో మొదటి సంతానం కలిగింది. జూలియస్ ఉద్యోగరీత్యా కుటుంబం దూర ప్రయాణం చెయ్యాల్సొచ్చింది. పార్వతీపురం, విశాఖపట్నం, అనంతపూర్, విజయవాడ, కర్నూలు, ఇలా వివిధ ప్రదేశాలు తిరుగుతూ, 1911 మొదట్లో ఇప్పటి ఒరిస్సాలోని ఛత్రపూరులో ఉండగా ఈథెల్ నెల తప్పింది. జూలియస్ సెలవు తీసుకొని కుటుంబ సమేతంగా ఇంగ్లాండు వచ్చాడు. 1912 జూన్ 23న లండన్లో ఆలన్ ట్యూరింగ్ పుట్టాడు.

మన దేశంలో వేడికి తట్టుకోలేక జబ్బుల పాలవుతారని, చదువుకోడానికి తగిన సదుపాయాలుండవనీని, పిల్లలు ఇంగ్లాండులోనే పెరగాలని తల్లిదండ్రులు నిశ్చయించారు. రెండేళ్ళయినా నిండని ఆలన్, నాలుగేళ్ళ వయసున్న జానీలని రిటైరయిన మిలిటరీ దంపతుల సంరక్షణలో పెట్టి వాళ్ళమ్మ 1913లో ఇండియా వెళ్ళి కొన్ని నెలల్లోనే జూలియస్‌తో కలిసి తిరిగి వచ్చింది. మొదటి ప్రపంచ యుద్ధం మూలంగా ప్రయాణం అపాయం కావడాన వాళ్ళమ్మ ఇంగ్లాండులో నిలిచి పోయింది. ఆ విధంగా యుద్ధం ఆలన్‌కి కలిసొచ్చింది. 1917 లో రీడింగ్ వితౌట్ టియర్స్ (Reading without Tears) అన్న పుస్తకం చూసి మూడు వారాల్లో తనంతట తానే చదవడం నేర్చుకున్నాడు. ప్రతి దీపస్తంభం దగ్గరా ఆగి దాని సీరియల్ నంబరు తెలుసుకునేవాడు. కుడి వైపేదో ఎడమ వైపేదో తెలిసేది కాదు. గుర్తుగా ఎడమ బొటనవ్రేలి మీద చుక్క పెట్టుకున్నాడు. 1919లో వాళ్ళమ్మ ఇండియా వెళ్తూ ఆలన్‌ని రిటైరయిన దంపతుల సంరక్షణలో మళ్ళీ పెట్టింది. తల్లిదండ్రులు చుట్టపుచూపుగా మాత్రమే వస్తూ పోవడంతో, పిల్లలు సరైన ఇంటి వాతావరణం అనేది లేకుండా పెరిగారు.

1921లో ట్యూరింగ్ వాళ్ళమ్మ ఇండియా నుండి తిరిగి వచ్చేటప్పటికి కొడుకు సరిగా ఎదగలేదని బాధపడింది. ఇతరులతో పెద్దగా కలవకుండా తనలో తను ఉండేవాడు. చదువు నిర్లక్ష్యం చేశాడు. తొమ్మిదేళ్ళు వచ్చినా ఇంకా భాగహారం చెయ్యడం తెలియదు. సరి చెయ్యగలిగినంత చేసి, హేౙెల్‌హర్స్ట్ ప్రిపరేటరీ బోర్డింగ్ స్కూల్లో చేర్చి తల్లిదండ్రులు మద్రాసు వెళ్ళారు. సగటు మార్కులతో ట్యూరింగ్ చదువు సాగించాడు.

పదేళ్ళ వయసున్న ట్యూరింగ్‌కి 1922లో ఎవరో ఎడ్విన్ బ్రూస్టర్ (Edwin Brewster) వ్రాసిన పుస్తకం (Natural Wonders Every Child Should Know) ఇచ్చారు. చిన్న పిల్లలకి కుతూహలం పెంచడానికి, సందేహాలు-సమాధానాల రూపంలో వ్రాసిన పుస్తకం: గుడ్డులోకి పిల్ల ఎలా వెళ్ళింది? అబ్బాయిలు బంతాటకీ అమ్మాయిలు బొమ్మలాటకీ ఎందుకిష్టపడతారు? ప్రపంచంలో మనం చూసే ప్రతి దానికీ కారణమంటూ ఉండాలనీ, దానికి దేవుడు కాక సైన్సు ఆధారమనీ ఆ పుస్తకం చెప్తుంది. ఈ పుస్తకం ట్యూరింగ్‌ని ఎంతో ప్రభావితం చేసింది. మొదటిసారిగా సైన్సు అనేదొకటి ఉందని దీని ద్వారానే తెలుసుకున్నాడు. రసాయన ప్రయోగాలు చేయడానికి ఎక్కువ ఉత్సాహం చూపెట్టేవాడు.

హైస్కూల్లో ట్యూరింగ్

1926 మే నెలలో పధ్నాలుగేళ్ళ వయసులో షెర్‌బోర్న్‌ బోర్డింగ్ స్కూల్లో చేరాడు. చేరే రోజునే చుట్టుపక్కల కలకలం సృష్టించాడు. సమ్మె మూలంగా రైళ్ళ రాకపోకలు రద్దయినా, ట్యూరింగ్ అరవై మైళ్ళు సైకిలు మీద ప్రయాణం చేసి బడికి చేరుకున్నాడు. కాని ఆ ఉత్సాహం ఎన్నాళ్ళో నిలవలేదు. షెర్‌బోర్న్‌ వాతావరణం అతని స్వతంత్ర భావాలకి సరిపడలేదు. స్నేహితులు తక్కువ. స్కూల్ రిపోర్టులు – పరిశుభ్రత తెలియదనీ, షర్టు మీద ఎప్పుడూ సిరా మరకలుంటాయనీ, చేతివ్రాత చదవలేమనీ – చూసి తండ్రి మండిపడేవాడు. అంత డబ్బు ఖర్చు చేసి పంపిస్తే కొడుకు సద్వినియోగ పరచుకోవడం లేదని. చాలా సబ్జెక్టులు శ్రద్ధగా చదివేవాడు కాదు. కాని కొన్నిసార్లు చదవకపోయినా పరీక్షల్లో అందరికన్నా మంచి మార్కులు తెచ్చుకునేవాడు – అది చూసి టీచర్లకి చిరాకు కలిగేది. తనకిష్టమైన గణితంలో బాగా చదివినా గుర్తించిన వాళ్ళు లేరు. అక్కడ ఆటలకిచ్చిన ప్రాధాన్యం చదువుకి, ముఖ్యంగా గణితాని కివ్వలేదు.

కాని ఒక టీచరు మాత్రం, ట్యూరింగ్ తెలివితేటలు గుర్తించి అతని మానాన అతన్ని వదిలి పెట్టాడు. అప్పుడు, 1928లో ట్యూరింగ్ ఐన్‌స్టయిన్ సాపేక్ష సిద్ధాంతం మీద సామాన్య పాఠకుల కోసం వ్రాసిన పుస్తకం చదివాడు. ఐన్‌స్టయిన్ కొన్ని వందల సంవత్సరాలగా వాడుకలో ఉన్న యూక్లిడ్ ప్రతిపాదించిన స్వయంసిద్ధ సత్యాలు (Euclid axioms) వాస్తవమా కాదా అని సందేహించడం ట్యూరింగ్‌కి నచ్చింది. కొన్ని సూత్రాలని ట్యూరింగ్ స్వయంగా రాబట్టి వాళ్ళమ్మకి వ్రాశాడు. 1929లో సర్ ఎడింగ్‌టన్ (Arthur Eddington) వ్రాసిన ది నేచర్ ఆఫ్ ఫిౙికల్ వర్ల్డ్ (The Nature of Physical World) కూడా చదివాడు.

అదే సమయంలో ట్యూరింగ్‌కి క్రిస్టఫర్ మార్కమ్ (Christopher Morcom) అన్న తోటి విద్యార్థితో పరిచయం అయింది. క్రిస్టఫర్ కూడా ఆలన్ లాగే సైన్సూ గణితాలలో దిట్ట. అంతే కాదు, అతను మిగిలిన సబ్జెక్టులలో కూడా రాణించాడు. చాలా శుభ్రంగా ఉండేవాడు. తనకన్నా అన్నిట్లోనూ మిన్నగా ఉన్న క్రిస్టొఫర్‌పై ఆలన్‌కి ఇష్టం కలిగి, ఆకర్షణ పెరిగి, గాఢమైన ప్రేమగా మారింది. అది చివరకి ఎలా పరిణమించేదో కాని, ఫిబ్రవరి 1930లో ఉబ్బసపు వ్యాధితో క్రిస్టఫర్ చనిపోయాడు. కానీ ఆలన్ జీవితాంతం క్రిస్టొఫర్ అతనికి ఆదర్శప్రాయుడయ్యాడు.

కాలేజ్ చదువు

ట్యూరింగ్ ఆపైన షెర్‌బోర్న్‌లో చివరి సంవత్సరాని కొచ్చేటప్పటికి చదువులో బాగా రాణించి, 1931లో కేంబ్రిడ్జ్ విశ్వవిద్యాలయం కింగ్స్ కాలేజీలో స్కాలర్షిప్ సంపాదించాడు. హైస్కూలు వాతావరణం కన్నా కేంబ్రిడ్జ్ వాతావరణం ట్యూరింగ్‌కి నచ్చింది. లిబరల్ విలువలు, అన్నింటికన్నా ముఖ్యంగా విజ్ఞానశాస్త్ర భావనలని ప్రోత్సహించే వాతావరణం అతని స్వభావానికి సరిపడింది. హైస్కూలులో ఎవరి పుస్తకాలు చదివి ప్రభావితమయ్యాడో వారిక్కడ తనకి ప్రొఫెసర్లు. ప్రపంచ ప్రసిద్ధి గాంచిన వాళ్ళు. వారిలో ఒకరు మన రామానుజన్‌ని తెప్పించుకున్న హార్డీ (G. H. Hardy) – సంఖ్యాశాస్త్రంలో ఉద్దండుడు. మరొకరు గణిత భౌతికశాస్త్రవేత్త సర్ ఆర్థర్ ఎడింగ్‌టన్ – ఐన్‌స్టయిన్ సాపేక్ష సిద్ధాంతాన్ని ప్రయోగాత్మకంగా నిరూపించిన వాడు. (అతనికీ అప్పుడే మన దేశం నుండి వచ్చిన యువ శాస్త్రవేత్త ఎస్. చంద్రశేఖర్‌కీ మధ్య నక్షత్రాలపై సిద్ధాంతాల గురించి పెద్ద వివాదాలు జరిగింది ఈ కాలం లోనే.)

1933 మార్చిలో ట్యూరింగ్, బెర్ట్రాండ్ రసెల్ (Bertrand Russel) గణితతాత్వికతపై వ్రాసిన పుస్తకం (An Introduction to Mathematical Philosophy) చదివాడు. రసెల్ పుస్తకం ముగిస్తూ ఒక్క విద్యార్థి అయినా ఈ పుస్తకం చేత ప్రభావితుడైతే లక్ష్యం నెరవేరినట్లేనన్నాడు. నవంబరుకల్లా ట్యూరింగ్ దాని మీద పెద్ద పెద్ద ప్రొఫెసర్ల ముందరే ఉపన్యాసమిచ్చాడు. గణితంలో అతని ప్రతిభ బాగా పెరిగింది.

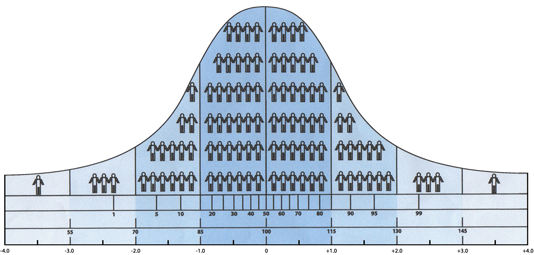
గాసియన్ వితరణ

ప్రకృతి లోనూ సాంఘిక జీవనం లోనూ పరిశోధనకి సంబంధించిన కొలతలని గ్రాఫు గీస్తే, అవి గంట ఆకారాన్ని పోలి ఉంటాయి. ఓ ప్రదేశంలో ఉష్ణోగ్రత, మనుషుల ఎత్తు, పువ్వుల సైజు, ఇలా చాలా కొలతలని చూస్తే అవన్నీ గంట ఆకారాన్ని కలిగి ఉంటాయి. దీన్ని గాసియన్ వితరణ (Gaussian distribution) అని పిలుస్తారు. సగటుకి ఎక్కువగా ఎన్ని ఉంటాయో తక్కువగా కూడా దాదాపు అన్నే ఉంటాయి. సగటుకి దూరంగా పోయే కొలదీ ఆ విలువ వున్నవి చాలా తక్కువ ఉంటాయి. ఇలా క్రమంగా ఉండటాన చాలా పరిశోధనలని సులువు చేస్తుంది – ఓ కొలత సగటు కన్నా చాలా తేడాగా ఉంటే దానికి ప్రాముఖ్యత ఉండొచ్చు.

కాని కొన్ని ముఖ్యమైన కొలతలు గంట ఆకారాన్ని పోలి ఉండవు. ఉదాహరణకి కుటుంబ ఆదాయం – కుబేరులు సగటుకు చాలా దూరంలో ఉంటారు, కుచేలులు సగటుకి దగ్గర్లో ఉంటారు. విచిత్రమైన విషయమేమిటంటే, అలాంటి కొలతల్లో కూడా, నమూనాగా (sample) వాటిల్లో కొన్ని తీసుకొని వాటి సగటు కనుక్కొని, మళ్ళీ ఇంకో నమూనాని తీసుకొని దాని సగటు కనుక్కొని, ఇలా నమూనాల సగటు విలువల గ్రాఫు గీస్తే అది గంట ఆకారంలో ఉంటుంది. దానిని బట్టి మనం అసలు కొలతల గురించి పరిశోధనలు సులువుగా చెయ్యవచ్చు. ఇది చాలా ఆశ్చర్యకరమైన విషయమే గాక, అనేక రంగాలలో చాలా ఉపయోగపడుతుంది. కొద్ది మందిని ఎవరికి ఓటు వేశారో అడిగి తెలుసుకొని జనాభా అంతా ఎలా ఓటు వేశారో చూచాయగా చెప్పవచ్చు. అలాగే ఓ మందు ప్రభావం తెలుసుకోడానికి ప్రజలందరి మీదా ప్రయోగాలు చెయ్యకుండా కొద్ది మందిమీదనే చేసి ఉజ్జాయింపుగా అందరికీ ఎలా వర్తిస్తుందో కనుక్కోవచ్చు. దీనిని సులభంగా వివరించే చక్కటి వీడియోని చూడండి.

అన్నిచోట్లా అగుపించే ఈ వితరణ గురించి ఎడింగ్‌టన్ తన లెక్చర్లలో పదే పదే చెప్పడంతో అది ట్యూరింగ్‌ని బాగా ఆకర్షించింది. కాని ఎడింగ్‌టన్ ఇచ్చిన వివరణ సంతృప్తికరంగా లేకపోవడంతో ట్యూరింగ్ నిర్దుష్టమైన గణితపరమైన వివరణ కోసం పరిశోధన మొదలు పెట్టి కొద్ది నెలల్లోనే సాధించాడు. దాని మీద ఓ వ్యాసం రాశాడు. కాని పాపం, కొన్నేళ్ళ క్రితమే, వేరొకరు అదే విషయాన్ని కనిపెట్టారనీ, దాని పేరు మధ్యమితి సిద్ధాంతమనీ (Central Limit Theorem) అనీ అతనికి తెలియదు. పూర్వం ఎవరన్నా దీని గురించి ఆలోచించారా లేదా అని పట్టించుకోకుండా స్వతంత్రంగా పరిశోధన చెయ్యడం ట్యూరింగ్ స్వభావం. అయినా విశ్వవిద్యాలయం వాళ్ళు అతని ప్రతిభని గుర్తించి, 1934లో ఫెలోషిప్ ఇచ్చారు. అతనికి మద్దతు ఇచ్చిన వారిలో కేన్స్ (John Maynard Keynes) ఒకరు. అప్పటికి ఆలన్ వయసు ఇరవై రెండేళ్ళు మాత్రమే.

కొద్ది కాలంలోనే theory of almost-periodic functions అనే ప్రత్యేక రంగంలో ఫాన్ నాయ్‌మన్ (John von Neumann: గత శతాబ్దంలో ఎంతో పేరుగాంచిన అరుదైన గణితవేత్త. అతని గురించి వచ్చే వ్యాసాలలో తెలుసుకుందాం.) పరిశోధనలని మెరుగుపరుస్తూ మరో పేపరు ప్రచురించాడు. ఇలా పనిచేస్తే ట్యూరింగ్ గణిత రంగంలో రాణించే వాడే కాని అతని పరిశోధనలు ఏ కొద్దిమందికో పరిమితమయి ఉండేవి. ఇవాళ మనం చెప్పుకునేటంతగా గొప్పవాడు కావడానికి కారణం అతను 1935 మొదట్లో ప్రొఫెసర్ న్యూమన్ (Max Newman) లెక్చర్లకి హాజరవడం.

న్యూమన్ పనిచేసింది స్థిరధర్మశాస్త్రం (Topology) అనే గణిత విభాగంలో. అది మనం చిన్నప్పుడు చదువుకున్న రేఖాగణితం (geometry) లోని రూపాలతో కూడుకున్నదే కాని ఓ ముఖ్యమైన తేడా ఉంది: ఈ రేఖ పొడవెంత, ఆ వృత్తం వ్యాసమెంత, ఆ రేఖల మధ్య కోణమెంత లాంటి కొలతలని పట్టించుకోకుండా ఈ భాగం ఆ భాగం పక్కపక్కన ఉన్నాయా, ఒక బిందువు నుండి మరో బిందువుని చేరుకునే మార్గముందా — ఇలాంటి వాటి గురించిన శాస్త్రం.

నాలుగు రంగుల్లో ప్రపంచం

టాపాలజీలో ఓ పేరున్న కుతూహలం కలిగించే సమస్య – నాలుగు రంగుల సమస్య. ప్రపంచ పటాన్ని తీసుకొని దాంట్లో పక్కపక్కనున్న దేశాలకి వేరేవేరే రంగులుండేటట్లుగా వెయ్యమన్నారనుకోండి. ఎన్ని రంగులు కావాలి? (దేశంలో పక్కపక్క రాష్ట్రాలు, రాష్ట్రంలో పక్కపక్క జిల్లాలు అన్నా అదే సమస్య.) 1852లో ఫ్రాన్సిస్ గత్రీ (Francis Guthrie) బ్రిటన్ పటానికి రంగులు వేస్తూ, నాలుగు రంగులు అవసరం అని కనుగొన్నాడు. ఎలాంటి పటానికైనా సరే నాలుగు సరిపోతాయి అని ప్రతిపాదించాడు. మరో వంద ఏళ్ళకి పైగా పండిత పామరులూ, గణితంలో హేమాహేమీలూ దీనిపై సాము చేశారు. వాస్తవమైన పటమైనా, ఊహా ప్రపంచానికి సంబంధించిందైనా, ఎలాంటి పటమైనా సరే, పక్క పక్క ప్రదేశాలకి వేరే వేరే రంగులుండేలా చెయ్యడానికి నాలుగు రంగులకి మించి అవసరం లేదు. నిరూపించలేకపోయినా అందు మూలంగా వేరే గణిత విభాగాలే పుట్టుకొచ్చాయి. ఎట్టకేలకు 1976లో దీనిని నిరూపించారు. కాని అది చాలా విచిత్రమైన నిరూపణ – కంప్యూటర్ సాయంతో నిరూపించిన మొదటి ముఖ్య గణిత సిద్ధాంతం.

న్యూమన్ 1928లో బొలోన్‌లో (Bologne) జరిగిన గణిత సమావేశానికి హాజరై హిల్బర్ట్ ప్రసంగం విన్నాడు. తర్వాత గోడెల్ హిల్బర్ట్ పథకాన్ని వమ్ము చెయ్యడం గురించి చదివాడు.

హిల్బర్ట్ పథకం మునుపటి వ్యాసం నుంచి స్థూలంగా గుర్తు తెచ్చుకుందాం. ఏ గణితశాస్త్రంలో నయినా కొద్ది స్వయంసిద్ధసత్యాలతో (axioms) మొదలుపెట్టి, తార్కిక నియమాలతో (rules of inference) ఆ శాస్త్రం లోని సిద్ధాంతాలనన్నిటినీ రాబట్టవచ్చు. ఉదాహరణకి సంఖ్యాశాస్త్రంలో:

• 0 సహజ సంఖ్య.
• ప్రతి సహజ సంఖ్య n కీ, దాని తరువాత సహజ సంఖ్య S(n) – Successor of n – ఉంటుంది.
• x, y, z సహజ సంఖ్యలలో x, y కీ, y, z కీ సమానమైతే, x, z కి సమానం.

ఇలా ఓ పది సూత్రాలకి మించవు. ఇవి సత్యాలంటే సహజంగానే అందరూ నమ్ముతారు. వీటి నుండి కొన్ని సిద్ధాంతాలని రాబట్టవచ్చు. ఆ సిద్ధాంతాలని ఉపయోగించుకొని మళ్ళా కొన్ని కొత్త సిద్ధాంతాలని రాబట్టవచ్చు. అబ్బురపడాల్సిన విషయమేమిటంటే, ఎంత జటిల సిద్ధాంతమైనా సరే ఇలా స్వయంసిద్ధసత్యాలతో మొదలెట్టి తార్కికంగా నిరూపించవచ్చు.

1928లో హిల్బర్ట్ గణిత ప్రపంచానికి మూడు ముఖ్యమైన ప్రశ్నలు వేశాడు:

1. గణితం సంపూర్ణమా (complete)? గణితంలో నిజమైన ప్రతిపాదనలన్నిటినీ స్వయంసిద్ధ సత్యాలతో మొదలుపెట్టి నిరూపించగలమా?
2. గణితం విరుద్ధ రహితమా (consistent)? స్వయంసిద్ధ సత్యాలతో మొదలెట్టి కొత్త సిద్ధాంతాలని రుజువుచేసే క్రమంలో 2 + 2 = 5 లాంటి విరుద్ధాలకి దారితీయదని నిక్కచ్చిగా చెప్పగలమా?
3. గణితం నిర్ధారణీయమా (decidable)? ఓ కచ్చితమైన పద్ధతి ద్వారా ఏ ప్రతిపాదన అయినా నిజమో కాదో చెప్పగలమా? దీనినే, హిల్బర్ట్ నిర్ణయ సమస్య (Hilbert’s Entscheidungsproblem అంటారు – decision problemకి జర్మన్) అందాం.

గణితవేత్తలనందరినీ పరిశోధించి రుజువు చెయ్యమనీ, అంతకన్నా ఉత్కృష్టమైన పని లేదనీ హిల్బర్ట్ ఉసి గొలిపాడు. ఈ మూడింటికీ సమాధానం అవును అనే హిల్బర్ట్ నమ్మాడు. కాని 1931లో గూడెల్ అన్న వియన్నా యువకుడు, మొదటి రెండు ప్రశ్నలకూ సమాధానం ‘కాదు’ అని రుజువు చేసి, అందరినీ విస్మయపరిచాడు. తన అసంపూర్ణ సిద్ధాంతంతో, సంఖ్యాశాస్త్రం లాంటి గణితవిభాగాల్లో, కొన్ని నిజమైన ప్రతిపాదనలని రుజువు చెయ్యలేమని రుజువు చేశాడు. అలాగే, సంఖ్యాశాస్త్రం విరుద్ధరహితమని నిరూపించలేమని నిరూపించాడు.

ఇక్కడ ఒక విషయం గమనించాలి; సంఖ్యాశాస్త్రం 2 + 2 = 5 లాంటి విరుద్ధాలకి దారి తీయవచ్చని గోడెల్ సిద్ధాంతం చెప్పదు; దారి తీయదు అని నిరూపించలేము అని మాత్రమే చెప్తుంది.

గూడెల్ అసంపూర్ణ సిద్ధాంతం హిల్బర్ట్ మూడో ప్రశ్నకి కూడా ‘కాదు’ అనే సమాధానం ఇవ్వలేదా అన్న సందేహం రావచ్చు. సూక్ష్మమైన తేడా ఉంది. గూడెల్ గణితంలో నిరూపించలేని సత్యాలున్నాయన్నాడు. హిల్బర్ట్ మూడో ప్రశ్నని కాస్త సవరించి, గణితంలో ఏదైనా ప్రతిపాదనని ఇచ్చినప్పుడు, దానిని నిరూపించగలమా లేదా అని చెప్పగలిగే యాంత్రిక పద్ధతి ఉన్నదా? అని అడిగితే దానికి గూడెల్ సిద్ధాంతం సమాధానం చెప్పలేదు. ఆ విధంగా అది విడిపడని సమస్యగానే మిగిలి ఉంది.

ఈ విషయాలు ఎంతో ఆసక్తికరంగా ఉండటంతో పాటు, వాటికీ తన రంగమయిన టాపాలజీకీ దగ్గరి సంబంధం ఉండటాన, న్యూమన్ 1935లో గణిత పునాదుల మీద కోర్సు మొదలెట్టి పాఠాలు చెప్పడం ప్రారంభించాడు. ట్యూరింగ్ ఆ కోర్సులో చేరాడు. గోడెల్ నిరూపణలు ఆ కోర్సుకి ముగింపు. మిగిలిపోయిన మూడో ప్రశ్న ట్యూరింగ్‌ని బాగా ఆకట్టుకుంది.

గణితం గురించి మాట్లాడేటప్పుడు ప్రతి మాటకీ స్పష్టమైన అందరూ ఒప్పుకున్న అర్థం ఉండాలి. మరి హిల్బర్ట్ నిర్ణయ సమస్యలో ‘యాంత్రిక పద్ధతి’ అంటే ఏమిటి? ఈ యాంత్రికం అన్న మాట ట్యూరింగ్ మనసులో నాటుకుపోయింది.

యాంత్రిక పద్ధతి

మాలతీ చందూర్ వంటలు-పిండి వంటలులో అమృతగుటకలు ఎలా చెయ్యాలో ఇలా చెప్తుంది:

1. బియ్యం ఒక గంటసేపు నీళ్ళలో నానవెయ్యి.
2. ఆపైన మెత్తగా కాటుకమాదిరి రుబ్బు.
3. సీమబాదం పప్పు ఓ పావుగంటసేపు నీళ్ళలో నానవెయ్యి.
4. వాటిపై తోలు తీసి సన్నగా చీలికలు మాదిరి తరుగు.
5. తరిగినముక్కల్ని నేతిలో వేయించు.
6. …

అలాగన్న మాట. మొత్తం అయేటప్పటికి బ్రహ్మాండమైన వంటకం తయారవుతుంది. రకరకాల వంటకాలు చెయ్యడానికి అడుగడుగునా చెయ్యవలసిన పనులు ఇలా స్పష్టంగా ఉంటాయి. మనమెవరం చేసినా, పుస్తకంలో చెప్పిన పద్ధతిని అక్షరాలా పాటిస్తే, వంటలో తేడా ఉండదు. అది యాంత్రికమని ఒప్పుకుంటారు కదా.

గణితంలో కూడా అంతే. అడుగడుగునా సులభమైన కూడికలూ, తీసివేతలూ, ఒకదానితో మరొకటి పోల్చడమూ చేస్తాము. వాటిని ఓ క్రమ పద్ధతిలో చేస్తే తగిన ఫలితం వస్తుంది. మనలో ఎవరం చేసినా ప్రతి అడుగుకీ చెప్పినట్లు చేస్తే వచ్చే ఫలితం ఒకటే. ఇదీ యాంత్రికమని ఒప్పుకుంటారు కదా. గణితంలో ఈ యాంత్రిక పద్ధతిని ఆల్గరిదమ్ (Algorithm) అంటారు – మధ్య యుగంలో బాగ్దాద్‌కి చెందిన అల్-ఖ్వారిౙ్‌మీ (Abu Abdullah Muhammad Ibn Musa Al-khwarizmi) అన్న పారశీక గణిత శాస్త్రజ్ఞుడి పేరు మీద. (ఇతను బీజగణితంలో కొన్ని ప్రక్రియలకీ మన దేశ గణాంక పద్ధతిని ప్రపంచమంతటా వ్యాప్తి చెందడానికీ ముఖ్య కారకుడు.)

దీనిని ఓ ఉదాహరణతో వివరిస్తాను. మీరంతా హైస్కూలులో గ.సా.భ. (గరిష్ట సామాన్య భాజకము, GCD – Greatest Common Divisor), క.సా.గు.ల (కనిష్ట సామాన్య గుణింతం, LCD – Least Common Divisor) గురించి చదువుకున్నారు. ఓ రెండు పూర్ణ సంఖ్యలిచ్చి (x, y), వాటి గ.సా.భ. కనుక్కోవాలంటే, దానికి రెండు వేల ఏళ్ళ క్రితం యూక్లిడ్ ఈ ఆల్గరిదమ్ ఇచ్చాడు:

1. if (x equals y) then Print x, Stop;
2. if (x is greater than y) then Set x = x – y; else Set y = y – x;
3. Go to Step 1;

మొదటి అడుగులో, రెండు సంఖ్యలనూ ఒక దానికొకటి పోల్చి, అవి సమానమైతే, అదే సమాధానమని చెప్పి పని ముగిస్తాము. సమానం కాకపోతే, రెండో అడుగుకెళ్ళి, పెద్ద సంఖ్య లోనుంచి చిన్న సంఖ్యని తీసివేసి, మూడో అడుగు కెళ్తాము. మూడో అడుగు మళ్ళా మొదటి అడుగుకి పంపిస్తుంది.

(x, y) విలువలు (15, 25) తో మొదలయితే, అవి (15, 10), (5, 10), (5, 5) అయి, సమాధానం 5 అని వస్తుంది.

(x, y) విలువలు (11, 3) తో మొదలయితే, అవి (8, 3), (5, 3), (2, 3), (2, 1), (1, 1) అయి, సమాధానం 1 అని వస్తుంది.

ఈ మూడడుగుల ఆల్గరిదమ్ ఎంతెంత పెద్ద సంఖ్యలిచ్చినా సరే, చివరకు సరైన సమాధానం ఇస్తుంది.

కాని హిల్బర్ట్ అడిగింది గ.సా.భ. లాంటి ఏదో ఒక గణిత సమస్యకి ఆల్గరిదమ్ కనుక్కోమని కాదు. గణితంలో ఏ ప్రతిపాదన చేసినా దానిని నిరూపించగలమో లేదో తేల్చి చెప్పే ఆల్గరిదమ్.

గణితంలో ఎందరో మేధావులు శతాబ్దాలుగా కృషి చేసినా సాధించలేని సమస్యలు కొన్ని ఉన్నాయి. సంఖ్యాగణితంలో మనకి ఆశ్చర్యం కలిగించే విషయం – వాటిలో కొన్నిటిని పదో తరగతి పిల్లలకి కూడా సులభంగా అర్థమయేలా చెప్పగలం. మచ్చుకొకటి: ప్రతి సరి సంఖ్య రెండు ప్రధాన సంఖ్యల కూడిక ఫలితం (every even number is a sum of two primes). దీనిని గోల్డ్‌బాఖ్ (Christian Goldbach) ప్రతిపాదించి రెండు వందల ఏళ్ళకి పైనే అయింది. మహామహులెందరో తమ జీవితమంతా శ్రమించారు కాని ఇంతవరకు ఇది నిజమో కాదో నిరూపించలేక పోయారు. హిల్బర్ట్ సమస్యని సాధించగలిగే ఆల్గరిదమ్ ఉంటే, దానికి ఈ ప్రతిపాదన ఇస్తే అది దీనిని నిరూపించగలమో లేదో చెప్తుంది. నిరూపించలేము అని తీర్పు చెప్తే, వృధా ప్రయాస తప్పుతుంది.

హిల్బర్ట్ ప్రణాళిక ప్రకారం గోల్డ్‌బాఖ్ ప్రతిపాదనల లాంటివెన్నిటినో అవలీలగా నిరూపించగలమో లేదో యాంత్రికంగా తేల్చి పారేయవచ్చు. గొప్ప గొప్ప మేధావులకే లొంగని సమస్యలని అంత తేలికగా తేల్చేసే విధానం ఉంటుందనుకోవడం వట్టి భ్రమ, అలాంటిదుంటే ఇక గణితవేత్తలెందుకు అని హార్డీ చిరాకు పడ్డాడు. గణితవేత్తలు కొత్త కొత్త సిద్ధాంతాలని ఏదో అద్భుత యంత్రం ముందు కూర్చొని దాని చక్రం తిప్పి కనుగొంటారని కలలు కనేది మరీ అమాయకులు మాత్రమేనని వేళాకోళం చేశాడు. నైపుణ్యం గల చేతి పనివాళ్ళంతా (కుమ్మరి, కమ్మరి, చేనేత) తమ తమ పనులని యంత్రాలు చెయ్యలేవని గొప్పలకి పోయి భ్రమపడి, చివరకు జీవనోపాధి కోల్పోవడం మనకి తెలిసిన విషయమే. (ఈ పనిమంతుడన్నది చివరకి నిజమయిందనుకోండి.) వేరే చూపుతో చూస్తే, గణితంలో రుజువులన్నీ, కొన్ని నియమిత సూత్రాలతో పకడ్బందీగా ఉంటాయి కాబట్టి, అందుకు యాంత్రిక పద్ధతి ఎందుకు ఉండకూడదు అని సందేహం వస్తుంది. ఉండే అవకాశమే లేదని హార్డీ లాగా ఎలా కొట్టి పారేయగలం?

ఆల్గరిదమ్ అంటే ఓ క్రమ వరుసలో అడుగడుక్కీ ఒక స్పష్టమైన పనిని యాంత్రికంగా చెయ్యగలగడం అని తెలుసుకున్నాం. ట్యూరింగ్ ఆ అడుగుల్లో ఏమున్నాయో అవతల బెట్టి వాటిని యాంత్రికంగా ఎవరైనా చేసేటప్పుడు వాళ్ళెలా చేస్తారో దాని మీద చూపు సారించాడు. అప్పుడు మనిషి చేసేది కొన్ని పరిమితమైన, చాలా సాధారణమైన సులభమైన చర్యలని గ్రహించాడు. మరి అవి అంత సులభమైనవయితే, మనిషికి బదులు యంత్రాన్ని వాడవచ్చు అని తీర్మానించి ఆ యంత్రం ఎలా ఉంటుందో కచ్చితంగా వర్ణించాడు. ఆ యంత్రంతో ఎన్నో పరికలనలు (computations) ఎలా చెయ్యవచ్చో చూపెట్టాడు. ఆల్గరిదమ్ వాడి, అంటే యాంత్రికంగా చెయ్యగలిగే పరికలనలు ఏవైనా ఆ యంత్రం చెయ్యగలదు అని ప్రతిపాదించాడు. అప్పుడు, ఆ యంత్రం చెయ్యలేని ఓ సమస్యని చూపెట్టాడు – అనగా ఆ సమస్యని సాధించే ఆల్గరిదమ్ లేదు. అంటే, హిల్బర్ట్ ఏ సమస్యనైనా సరే తీర్చే యాంత్రిక పద్ధతి ఉందా? అన్న ప్రశ్నకు సమాధానం, ‘లేదు’ అని అర్థం – ఆల్గరిదమ్ లేని సమస్య ఒకదానిని చూపెట్టాడు కనుక. ఈ పరిశోధనలో ఉపఫలితంగా, అన్ని రకాల పరికలనలు చేసే యంత్రానికి గణిత పరమైన నమూనాని కనుక్కున్నాడు. ఇదంతా ఎలా చేశాడో కాస్త లోతుగా తెలుసుకుందాం.

నిత్యజీవితంలో పరికలనం

ట్యూరింగ్ కాలం నాటికి కంప్యూటర్లు లేవు. మనుషులే (ఎక్కువగా ఆడవాళ్ళు) లెక్కలు చేసేవాళ్ళు. ఎట్లా చేస్తారో ట్యూరింగ్ జాగ్రత్తగా ఆలోచించాడు. లెక్కలు చేసే అమ్మాయి అసలు ఏం చేస్తుంది? ఓ కాగితం మీద గుర్తులు వేయడం, కొన్నిటిని చెరిపేసో కొట్టేసో, వేరే గుర్తులు వేయడం. అంతే కదా? అలా చేసేటప్పుడు, ముందర తన చూపు కొన్ని గుర్తుల మీద ఉంచుతుంది, మరి కాసేపటికి చూపు పక్క గుర్తుల మీదకు సాగుతుంది. ఈ విధానంలో అక్కరలేని ప్రక్రియలనన్నిటినీ, ట్యూరింగ్ అవతల పెట్టాడు – అమ్మాయి మధ్యలో కాఫీ తాగుతోందా, సంగీతం వింటోందా, ఇలాంటివన్నీ అనవసరం. అలాగే వాడేది పెన్నా, పెన్సిలా అన్నదీ అనవసరమే. చేసే లెక్కని బట్టి, సరిపడా కాగితాలు కావాలి. ఓ పేజీ నిండితే కొత్త పేజీకి వెళ్తుంది. ఒక్కొక్కప్పుడు, ఇంతకు ముందు పేజీలలో ఏముందో చూడాల్సి రావచ్చు. పేజీలున్న పుస్తకం కాకుండా, కావలసినన్ని గడులున్న కాగితపు టేపు మీద లెక్క చేసిందనుకోండి. ఫలితంలో తేడా ఉండదు గదా.

నిర్దిష్టమైన ఓ ఉదాహరణ తీసుకుందాం. రెండు సంఖ్యలని గుణించాలంటే ఏం చేస్తుంది?

     125
X 53
——–

        375
+ 6250
———
= 6625

అలా కాగితం మీద నిలువుగా కాకుండా దానినే రూళ్ళు ఉన్న కాగితపు టేపు మీద ఇలా వ్రాస్తుంది:

1

2

5

X

5

3

=

3

7

5

+

6

2

5

0

=

6

6

2

5

ఇలా అడ్డంగా ఒకే వరుసలో లెక్క చెయ్యడం కాస్త చిరాకుగా ఉండవచ్చు గాని, అదేం పెద్ద సమస్య కాదని ట్యూరింగ్ నమ్మాడు. ఈ గుణింతాన్ని అమ్మాయి కాగితపు టేపు మీద ఎలా చేస్తుందో జాగ్రత్తగా గమనిద్దాం. చూపు మొదటి రెండు అంకెల (5, 3) మీద పెడుతుంది.

1

2

5

X

5

3

=

ముందర హెచ్చించి తర్వాత కూడితే కదా ఫలితం వచ్చేది. హెచ్చిస్తే వచ్చేది 15, కాని దాంట్లో 5 మాత్రమే టేపు మీద రాసి, 1 అన్నది మిగులుగా మనసులో గుర్తు పెట్టుకుంటుంది:

1

2

5

X

5

3

=

5

ఇప్పుడు తన చూపు వేటి మీద పెడుతుంది? మొదటి సంఖ్య లోని రెండో అంకె (2) మీద, రెండో సంఖ్య లోని మొదటి అంకె (3) మీద:

1

2

5

X

5

3

=

5

ఇంకా హెచ్చించే దశలోనే ఉన్నది కనుక, వీటి ఫలితం 6 గా గుర్తించి, మనసులో ఉన్న మిగులుతో పాటు ఫలితం 7 అని 5 పక్క గడిలో రాస్తుంది:

1

2

5

X

5

3

=

7

5

ఇలా హెచ్చించే దశ పూర్తి అయింతర్వాత, వచ్చిన రెండు పాక్షిక ఫలితాలని కూడాలి. అంటే ఇది కూడే దశ అని అమ్మాయి మనసులో గుర్తు పెట్టుకొని, చూపు ఆ ఫలితాల మొదటి అంకెల (5, 0) మీద పెడుతుంది:

1

2

5

X

5

3

=

3

7

5

+

6

2

5

0

=

వాటిని కూడిన ఫలితం 5 అని టేపు మీద గుర్తు పెట్టి, ఇప్పుడు మిగులు 0 అని మనసులో ఉంచుకుంటుంది:

1

2

5

X

5

3

=

3

7

5

+

6

2

5

0

=

5

తర్వాత చూపు (7, 5) మీద పెట్టి, ఫలితాన్ని నమోదు చేసి, చూపు (3, 2) మీదకు మరలుస్తుంది:

1

2

5

X

5

3

=

3

7

5

+

6

2

5

0

=

2

5

ఇంతకు ముందు (2, 3) అంకెలని చూసినప్పుడు అప్పుడు ఉన్నది హెచ్చించే దశ, కాని ఇప్పుడు ఉన్నది కూడే దశ. వాటిని కూడి, మిగులు 1 అని మనసులో ఉండటాన, ఫలితం 6 అని నమోదు చేస్తుంది:

1

2

5

X

5

3

=

3

7

5

+

6

2

5

0

=

6

2

5

అడుగడుగడుగునా ఇలా వివరించడం, మీకు కొంత విసుగు కలిగించి ఉండవచ్చు కాని, దీని వలన మనకేమి అర్థమయింది?

• మన చూపు ఎప్పుడూ కొద్ది గుర్తుల మీదనే నిలిచి ఉంటుంది. పై ఉదాహరణలో మూడుకి మించలేదు.
• ప్రతి అడుగుకీ మనం తీసుకునే చర్య, కేవలం అప్పుడు మన చూపులో ఉన్న గుర్తుల మీదా, మనఃస్థితి మీదా మాత్రమే ఆధారపడి ఉంటుంది. (పై ఉదాహరణలో మనఃస్థితి అంటే, హెచ్చించే దశలో ఉన్నామా, కూడే దశలో ఉన్నామా, మిగులు ఉందా అని.)

ఒకే సమయంలో ఎన్ని గుర్తుల మీద చూపు పెట్టగలం? అది మనిషి మనిషికీ వేరుగా ఉన్నా, అనేకం కాదు – పది పదహారుకి మించవు. కాని లెక్క (కంప్యుటేషన్) సరిగ్గా చెయ్యడానికి ఒక్క సమయంలో ఎన్ని గుర్తుల మీద చూపు నిలపెట్టగలగాలి? ఒకే ఒక్కటి. ఇది మీకు కొంత ఆశ్చర్యం కలిగించి ఉండొచ్చు. కాని వేరే చోట ఉన్న గుర్తు కావాలంటే మనం ఒక గడి తర్వాత మరొకటి దాటుకుంటూ పోయి దానిని పరిశీలించవచ్చు. లెక్క సరిగ్గా చెయ్యడానికి ఎన్ని మనఃస్థితులు కావాలి అంటే అది చెయ్యవలసిన లెక్క మీద ఆధారపడి ఉంటుంది. ఈ విశ్లేషణతో ఇప్పుడు మనం ఎలాంటి కంప్యుటేషన్ అయినా సరే అతి సరళమైన ఈ క్రింది చర్యలతో చేసెయ్యవచ్చు:

• గడులు వున్న కాగితపు టేపు మీద కొన్ని గుర్తులు రాసుకోవాలి.
• ఏ సమయానా, చూపు ఒకే ఒక్క గడి మీద ఉంటుంది.
• తరువాత చెయ్యవలసిన పని, ప్రస్తుత స్థితి మీదా, చూసిన గుర్తు మీదా ఆధారపడి ఉంటుంది. కేవలం ఆ రెంటి మీదనే.
• ఆ పని ఏమిటి? అవసరమైతే ఆ గడిలో వేరే గుర్తు పెట్టి, స్థితి మారి, కుడి వైపో ఎడమ వైపో పక్కనున్న గడికి జరగడం, కాకపోతే ఆగిపోవడం.

ప్రతి అడుగుకీ చెయ్యవలసిన పని కేవలం ఓ గుర్తుని చదవడం, అవసరమైతే దాని స్థానంలో వేరే గుర్తుని రాసి, స్థితి మారి అటో ఇటో కదలడం. అంతే. ఈ మాత్రం చెయ్యడానికి మనిషి ఎందుకు, ఓ యంత్రాన్ని పెడితే సరిపోతుంది గదా. అదీ ట్యూరింగ్ ఆలోచన. ఆ యంత్రానికి కావాల్సింది సరిపడా గడులున్న కాగితపు టేప్, తల స్థానాన్ని ఒక గడి నుండి పక్క గడికి మార్చ గలగడం, ఉన్న గడిలో గుర్తుని చూసి వేరే గుర్తుని రాయగలగడం. మనిషి మనఃస్థితులని ఈ యంత్రం యాంత్రికస్థితులుగా (configurations) అనుసరించాలి.

ఇది కారు లాంటి యంత్రమా? గేర్లు ఉంటాయా? కరెంటు మీద నడుస్తుందా, బ్యాటరీ మీదనా? ఇవేవీ ముఖ్యం కాదు. ఇది కేవలం గణిత భావానికి ఆకారం ఇవ్వడం. పోయి నిర్మించాలని లేదు. కాని ముఖ్యంగా గ్రహించాల్సింది – ఎలాంటి ఆల్గరిదమ్ అయినా సరే ఇలాంటి యంత్రంతో చేసెయ్యవచ్చు. మీకది నమశక్యం కాదంటే నేనర్థం చేసుకోగలను. మీకు నమ్మకం కలగాలంటే యంత్రాలతో కొన్ని లెక్కలు చేయించాలి.

ట్యూరింగ్ యంత్రాలు

ట్యూరింగ్ యంత్రం ప్రతి అడుగుకీ చెయ్యవలసిన పనిని క్లుపంగా ఐదుపాళ్ళ అంశంతో (quintuple) వర్ణించవచ్చు. కొన్ని ఐదుపాళ్ళ అంశల ఉదాహరణలు, వాటి అర్థాలు:

1. (S1, a, b, S2, R) : S1 స్థితి లో ఉన్నప్పుడు, ప్రస్తుత గడిలో గుర్తు a అయితే, ఆ గడిలో b రాసి, S2 స్థితి కి మారి కుడి వైపు గడిలోకి జరుగు.
2. (S1, a, b, S2, L) : దీనికీ పైదానికీ తేడా అల్లా, కుడి వైపుకి బదులు ఎడమ వైపుకి జరగాలి.
3. (S1, a, b, S2, N) : దీనికీ మొదటి దానికీ తేడా అల్లా, జరగకుండా (N for No Move) ఉన్న గడిలోనే ఉండాలి.
4. (S1, a, a, S2, R) : చూసిన గుర్తునే తిరిగి రాస్తున్నాం అంటే చూసిన గడిని మార్చడం లేదని అర్థం.
5. (S1, #, a, S2, R) : ప్రస్తుత గడి ఖాళీ గా ఉంటే, దాంట్లో a రాయి. (ఖాళీ గడిని # గుర్తుతో సూచిస్తున్నాం.)
6. (S1, a, #, S2, R) : ప్రస్తుత గడి లో a ఉంటే, దానిని చెరిపేయి – అంటే దాని స్థానంలో ఖాళీ గుర్తుని రాయి.

కూడిక యంత్రం

ట్యూరింగ్ యంత్రాలని అర్థం చేసుకోడానికి మనమో చిన్న కూడిక యంత్రాన్ని తయారు చేద్దాం. తయారు చెయ్యడమంటే ఏమిటి? దాని స్థితులనీ, కదలికలనీ నిర్వచించే ఐదుపాళ్ళ అంశల పట్టిక తయారుచెయ్యడమే. (స్థితులలో ఒకదానిని మొదటి స్థితిగా గుర్తించాలి – యంత్రం ఆ స్థితిలో మొదలవుతుంది.) ఈ కూడిక యంత్రం, టేపు మీద ఉన్న రెండు సంఖ్యల్ని (M, N) కూడి వాటి స్థానంలో ఫలితాన్ని (M+N) రాయాలి. సులభంగా ఉండటానికి, ఆ సంఖ్యలు దశాంశ పద్ధతి లో కాకుండా కేవలం ఒంటి గణితంలో ఉన్నాయనుకుందాం. రెండూ, మూడూ కూడితే ఐదు కదా. టేపు మీద 11#111 ఇస్తే, యంత్రం 11111 ని ఫలితంగా ఇవ్వాలి:

దీనిని సులభంగా చెయ్యడం ఎలా? మొదటి సంఖ్యలో వరుసగా ఉన్న రెండు ఒకట్లనీ కుడి వైపు ఒక గడి మాత్రం జరిపితే సరిపోతుంది. కాని మన యంత్రానికి అలా గళ్ళ సముదాయాన్నంతటినీ ఒకేసారి జరపడం ఎలాగో తెలియదు. తెలిసిందల్లా, ఉన్న గడి మీద గుర్తు రాయడం, కుడి వైపు గడికో ఎడమ వైపు గడికో కదలడం. కాబట్టి మొదటి సంఖ్య లోని మొదటి అంకెని # గా మార్చి, కుడి వైపు ఒక్కో గడి దాటుకుంటూ రెండు సంఖ్యల మధ్యన ఉన్న # ని 1 గా మారిస్తే సరైన ఫలితం వస్తుందని గ్రహించవచ్చు. మొదటి సంఖ్యలోని మొదటి అంకెని చేరడానికి ఓ స్థితీ, దానిని మార్చింతర్వాత ఆ సంఖ్య గడులన్నీ దాటడానికి మరో స్థితీ, చివరన రెంటినీ విభజిస్తున్న # ని మార్చినప్పుడు మరో స్థితీ ఉంటే సరిపోతుంది. ఈ చర్యలని క్రింది పట్టికలో చూడవచ్చు:

# మీద చర్యలు	వివరణ	1 మీద చర్యలు	వివరణ
(S1, #, #, S1, R)	మొదటి సంఖ్యకి చేరేదాకా కుడి వైపు కదులు. (1)	(S1, 1, #, S2, R)	మొదటి సంఖ్యలో మొదటి అంకెకి చేరాం. 1 ని # చేసి, S2 కి మారి కుడి వైపు కదులు. (2)
(S2, #, 1, S3, R)	మొదటి సంఖ్యని దాటి విభజన గడికి చేరాం. # ని 1 చేసి, S3 కి మారి కుడి వైపు కదులు. (4)	(S2, 1, 1, S2, R)	మొదటి సంఖ్య చివరిదాకా, 1 ని మార్చకుండా కుడి వైపు కదులు. (3)

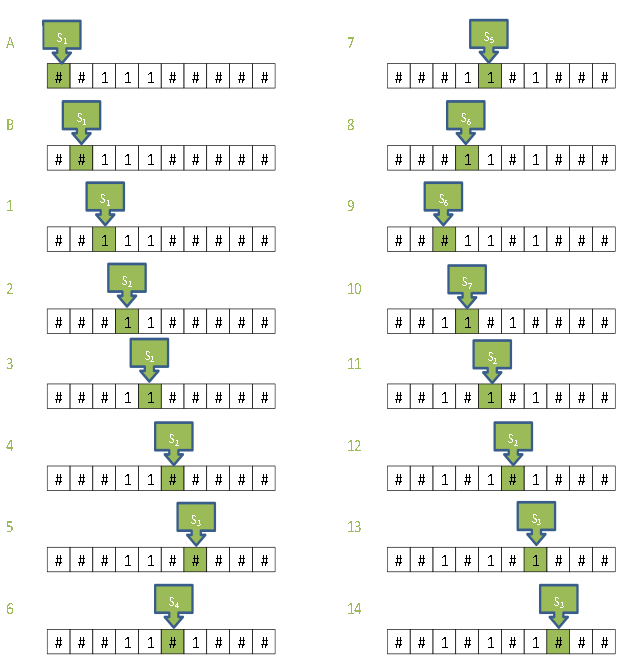
పై పట్టికలో S3 స్థితికి సంబంధించిన చర్యలు లేవు. యంత్రం ఆ స్థితిలో ఉన్నప్పుడు, పట్టికలో దానికి చర్యలు లేవు కనుక ఆగిపోతుంది. టేపు మీద, సంఖ్యలు రెండు, మూడు ఇస్తే, యంత్రం పై పట్టిక ప్రకారం అడుగడుక్కీ ఏం చేస్తుందో ఈ క్రింది బొమ్మలో చూడవచ్చు (పట్టికలో వివరణతో పాటు బ్రాకెట్లలో, బొమ్మలో కొన్ని కదలికల్ని సూచించాను):

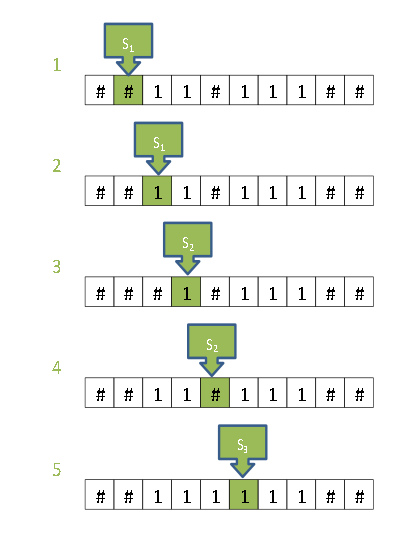
ఓ గడిలో 1 ని చెరిపేసి, మరో ఖాళీ గడిలో 1 రాసి, దీన్నో పెద్ద కూడిక యంత్రంగా వర్ణిస్తున్నానని తీసి పారేయకండి. ఇది చాలా అల్పమైన యంత్రమే. కాని గమనించండి, నాలుగంటే నాలుగు అయిదింతలతో మనమీ యంత్రం పని తీరుని పూర్తిగా వర్ణించాము. అంతకు మించి మనం చెయ్యాల్సిందేమీ లేదు. కావలసినన్ని గళ్ళున్న టేపునిస్తే, ఇది ఎంత పెద్ద సంఖ్యలనైనా కూడి సరైన సమాధానం ఇస్తుంది.

కూడికలు సులభమే, హెచ్చవేతలు చెయ్యగలదా? ట్యూరింగ్ యంత్రంతో ఎలా చెయ్యగలమో ఆలోచించండి. టేపు మీద #11#111# ఇస్తే సమాధానం #111111# రావాలి (2×3=6 కనుక). కూడికలంత సులభం కాదు. కాని ఓ కిటుకు చెప్తాను. కాపీ చెయ్యడం ఎలాగో తెలిస్తే, అప్పుడు కాస్త తేలిక: మొదటి గ్రూపులో ఉన్న 1 గళ్ళని టేపులో వేరే చోటకి కాపీ చెయ్యాలి. రెండో గ్రూపులో ఎన్ని 1 గళ్ళు ఉంటే అన్ని సార్లు కాపీ చేస్తే సరిపోతుంది. అయితే ముందర కాపీ యంత్రాన్ని తయారు చేద్దాం. అంటే దాని కదలిక పట్టికని తయారుచెయ్యడం. టేపు మీద #111# ఇస్తే కాపీ యంత్రం చివరకి #111#111# ఇవ్వాలి. వివరించేటప్పుడు మొదటి సంఖ్యని N అనీ కొత్తగా కాపీ చేసిన సంఖ్యని P అనీ అందాం.

కాపీ యంత్రం

# మీద చర్యలు	వివరణ	1 మీద చర్యలు	వివరణ
(S1, #, #, S1, R)	మొదటి సంఖ్య ని (N) చేరే దాకా కుడి వైపు కదులు. (A, B)	(S1, 1, #, S2, R)	మొదటి సంఖ్య లో (N) మొదటి అంకె కి చేరాం. 1 ని # చేసి, S2 కి మారి కుడి వైపు కదులు. (1)
(S2, #, #, S3, R)	విభజన గుర్తు చేరాం. దాటి కుడి వైపు కదులు. (4, 12, 20)	(S2, 1, S2, R)	మొదటి సంఖ్య చివరిదాకా, 1 ని మార్చకుండా కుడి వైపు కదులు. (2, 3, 11)
(S3, #, 1, S4, L)	రెండో సంఖ్య (P) కుడి చివర్న 1 కాపీ చెయ్యి. (5, 14, 23)	(S3, 1, 1, S3, R)	రెండో సంఖ్య (P) కుడి చివర దాకా కదులు. (13, 21, 22)
(S4, #, #, S5, L)	విభజన గుర్తు చేరాం. S5 కి మారి ఎడమ వైపు కదులు. (6, 16, 26)	(S4, 1, 1, S4, L)	రెండో సంఖ్య (P) ని దాటుకుంటూ ఎడమ వైపు కదులు. (15, 24, 25)
(S5, #, 1, S8, L)	విభజన గుర్తుకి వెంటనే ఎడమ వైపున # చూశాం. అంటే N లో అన్ని అంకెలనీ కాపీ చేశాం. తిరిగి 1 రాసి, ఎడమ వైపు కదులు. (27)	(S5, 1, 1, S6, L)	విభజన గుర్తు కి వెంటనే ఎడమ వైపున 1 చూశాం. S6 కి మారి ఎడమ వైపు కదులు. (7, 17)
(S6, #, 1, S7, R)	# గుర్తుని కుడి వైపు జరపడం మొదలెట్టు. (9, 18)	(S6, 1, 1, S6, L)	N లో అన్ని అంకెలనీ దాటుకుంటూ ఎడమ వైపు కదులు. (8)
(S7, #, #, N, N)	Not encountered.	(S7, 1, #, S2, R)	# గుర్తుని కుడి వైపు జరిపాం. 1 ని కాపీ చెయ్యడం తిరిగి మొదలెట్టు. (10, 19)
(S8, #, #, N)	కాపీ పూర్తయింది. (30)	(S8, 1, 1, S8, L)	N లో అన్ని అంకెలనీ దాటుకుంటూ ఎడమ వైపు కదులు. (28, 29)

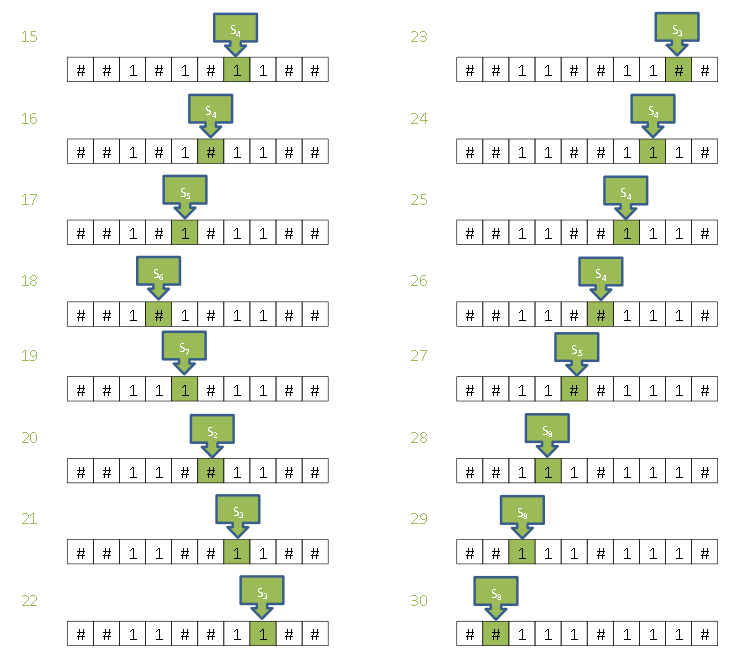
టేపు మీద #111# ఇస్తే, యంత్రం దానిని కాపీ చేసి, #111#111# గా ఎలా ఇస్తుందో, ప్రతి కదలికతో సహా క్రింది బొమ్మలో చూడవచ్చు. యంత్రం కుడి వైపు కదలుతూ మొదటి సంఖ్యలోని మొదటి అంకెని చేరుకుంటుంది. దానిని ఖాళీ గా మార్చి, కుడి వైపు కదలుతూ మొదటి సంఖ్యని దాటుతుంది. మరొక గడి దాటి, అక్కడ 1 కాపీ చేస్తుంది. ఇప్పుడు ఎడమ వైపు కదలుతూ రెండు సంఖ్యల మధ్య విభజన రేఖని చేరుతుంది. ఇంకా ఎడమ వైపు సాగి మొదటి సంఖ్యలో ఎక్కడ పోయిన సారి కాపీచేశామో అక్కడకి చేరి (అది ఖాళీగా గుర్తు పెట్టుకున్నాం), దానిని 1 చేసి, కుడి వైపుకి జరిగి అక్కడ 1 ఉంటే మరలా పైన చెప్పినట్లు తిరిగి కాపీ మొదలెడతాం. పట్టికనీ బొమ్మనీ కలిపి జాగ్రత్తగా పరిశీలిస్తే ఇది సరిగా కాపీ చేస్తుందని మీరు రూఢి పరచుకోవచ్చు. (ఇంతకు ముందు లాగానే, పట్టికలో వివరణతో పాటు బ్రాకెట్లలో, బొమ్మలో కొన్ని కదలికల్ని సూచించాను)

హెచ్చవేత యంత్రం

హెచ్చవేత యంత్రం టేపు మీద #11#111# ఇస్తే చివరకి #11#111#111111# ఇవ్వాలి. ఈ సంఖ్యలని, M, N, P అని పిలుద్దాం. N ని M సార్లు కాపీ చెయ్యాలి. మొదటి సారి కాపీ చేసేటప్పుడు M మొదటి అంకె స్థానంలో 1 కి బదులు #, రెండో సారి కాపీ చేసేటప్పుడు M రెండో అంకె స్థానంలో 1 కి బదులు #, అలా # ని జరుపుకుంటూ పోవాలి. అది విభజన గుర్తుకి చేరిందంటే తగినన్ని సార్లు కాపీ చేసినట్లు. అందుకు S10, S11, …, S15 స్థితులు వాడుదాం. (S10 హెచ్చవేత యంత్రం మొదటి స్థితి.) కాపీ చెయ్యడానికి సిద్దమయినప్పుడు, S11 నుండి S1 స్థితిలోకి మారుతుంది. S1 కాపీ యంత్రం మొదటి స్థితి అని గమనించండి. కాపీ యంత్రం చర్యలు ముగిసేటప్పటికి S8 స్థితిలో ఉంటుంది. ఆ స్థితిలో ఆగిపోకుండా (కేవలం ఒక కాపీ అయితే ఆగవచ్చు), తరువాత కాపీ చెయ్యడానికి చర్యలు (అంటే M లో # ని జరపడం) చెయ్యాలి.

# మీద చర్యలు	వివరణ	1 మీద చర్యలు	వివరణ
(S10, #, #, S10, R)	మొదటి సంఖ్య (M) లో ఎడమ చివరి అంకె 1 చేరేదాకా కుడి వైపు కదులు. (101)	(S10, 1, #, S11, R)	మొదటి సంఖ్య (M) లో మొదటి అంకె కి చేరాం. 1 ని # చేసి, కుడి వైపు కదులు. (102)
(S11, #, #, S1, R)	M కీ N కీ మధ్య విభజన గడికి చేరాం. S1 కి మారడం ద్వారా కాపీ మొదలెట్టు. (104, 138)	(S11, 1, S11, R)	M లో అంకెలని దాటుకుంటూ కుడి వైపు కదులు. (103)
(S8, #, #, S12, L)	N కీ M కీ మధ్య విభజన గడికి చేరాం. ఎడమ వైపు కదులు. కాపీ పూర్తయింది. (134, 185)	(S8, 1, 1, S8, L)	N ఎడమ చివరకు కదులు. (బొమ్మలో లేదు)
(S12, #, 1, S15, L)	N కీ M కీ మధ్య విభజన గడికి ఎడమ పక్కన # గుర్తుకి చేరాం. అంటే హెచ్చవేయడం పూర్తయింది. 1 ని తిరిగి ఇచ్చి ఎడమ వైపు కదులు. (186)	(S12, 1, 1, S13, L)	N కీ M కీ మధ్య విభజన గడికి ఎడమ పక్కన M లోని 1 గుర్తుకి చేరాం. S13 అంటే కి మారు. (135)
(S13, #, 1, S14, R)	M లో # గుర్తు ని కుడి వైపు జరపడం మొదలెట్టు. (136)	(S13, 1, S13, L)	M లో అన్ని అంకెలనీ దాటుకుంటూ ఎడమ వైపు కదులు. (బొమ్మలో లేదు)
(S14, #, N, N)	Not encountered.	(S14, 1, #, S11, R)	M లో # గుర్తు ని కుడి వైపు జరపడం పూర్తిచెయ్యి. కాపీ చెయ్యడం తిరిగి మొదలెట్టు. (137)
(S15, #, #, N)	హెచ్చవేత పూర్తయింది. ఆగు.
(S15, 1, 1, S15, L)	M లో అన్ని అంకెలనీ దాటుకుంటూ ఎడమ వైపు కదులు. (187)

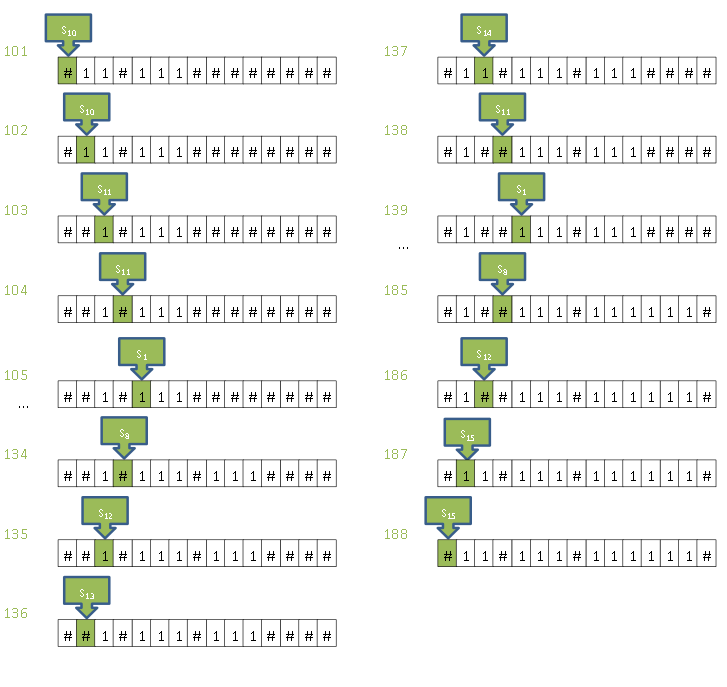
క్రింది బొమ్మని చూడండి. 2×3=6 అని చెయ్యడానికి 88 అడుగులు (101 నుండి 188 దాకా) తీసుకుంది. 105 అడుగులో S1 కి మారింతర్వాత 134 దాకా కాపీ యంత్రం చర్యలే; అలాగే 139 నుండి 185 దాకా (… ద్వారా సూచించాను).

దశాంశ పద్ధతిలో కూడే యంత్రం

ఇలా ఒంటి గణితం కాకుండా మనం రోజూ వాడే దశాంశ పద్ధతిలో ట్యూరింగ్ యంత్రం పనిచేస్తుందా అంటే, తప్పకుండా. టూకీగా కూడిక యంత్రం ఎలా పని చేస్తుందో ఓ ఉదాహరణతో (736 + 45 = 781) చెప్తాను:

#

#

#

#

#

!

7

3

6

+

4

5

#

#

#

#

#

#

#

1

!

7

3

#

+

4

#

#

#

#

#

#

#

8

1

!

7

#

#

+

#

#

#

#

#

#

#

7

8

1

!

#

#

#

#

#

#

#

#

#

యంత్రం టేపు మీద 7 ఉన్న గడిలో మొదలవుతుంది. మొదటి సంఖ్యలో కుడి చివరి అంకెకి వెళ్ళాలి: కుడి వైపుకి జరుగుతూ, స్థితి మారకుండా + ఉన్న గడి దాకా వస్తుంది; అప్పుడు ఎడమ వైపుకి జరిగి, అక్కడ ఉన్న అంకె (6) స్థానంలో # వ్రాసి, ఆ అంకెని గుర్తుంచుకుంటుంది. ఎలా? వేరే స్థితిలోకి మారి. అక్కడ 0 నుండి 9 దాకా ఏ అంకె అయినా ఉండవచ్చు కనుక గుర్తుంచుకోడానికి పది స్థితులు ఉండాలి. రెండవ సంఖ్యలో కుడి చివరి అంకెకి వెళ్ళాలి: కుడి వైపు జరుగుతూ + ఉన్న గడిని దాటి రెండో సంఖ్య అంకెలన్నీ దాటుకుంటూ చివరకు # చూసింతర్వాత, ఎడమ వైపుకి జరిగి, అక్కడ ఉన్న అంకె (5) గడిని చేరుతుంది. దాని స్థానంలో # వ్రాసి, కూడిక ఫలితాన్ని గుర్తుంచుకోడానికి వేరే స్థితికి మారుతుంది. ఫలితం 0 నుండి 9 దాకా ఉండవచ్చు; పైగా మిగులు ఉందా లేదా అని గుర్తుంచుకోవాలి. అంటే ఫలితం 10*2=20 రకాలుగా ఉంటుంది కనుక 20 వేరే స్థితులు కావాలి. అప్పుడు యంత్రం ఎడమ వైపుకు జరుగుతూ ! దాటి # చేరుకున్న తరువాత, ఫలితాన్ని (1) నమోదు చేస్తుంది. ఇప్పుడు టేపు ఎలా ఉంటుందో బొమ్మలో రెండో వరుసలో చూడవచ్చు.

పైన చేసిందాన్నే మళ్ళీ చెయ్యాలి – కాని ఇప్పుడు కుడి చివరి అంకెలు 3, 4. వాటిని కూడి, ఇంతకుముందు మిగులు ఉండటాన, ఫలితాన్ని 8 గా నమోదు చేస్తుంది (బొమ్మలో మూడో వరుస). ఇలా చేస్తూ, చివరకి ఓ సంఖ్యలో అంకెలన్నీ అయిపోతే, వేరే సంఖ్యలో మిగిలిపోయిన అంకెలని కాపీ చెయ్యాలి (7), మిగులు ఉంటే దానిని కూడి. చివరకి టేపు మీద మిగిలేది కూడిక ఫలితం (బొమ్మలో చివరి వరుస). అప్పుడు యంత్రం ఆగుతుంది.

దీనికి పట్టిక ఎంతుంటుందో ఊహించుకోండి. కొన్ని డజన్లకి పైగా స్థితులు, ప్రతి స్థితికీ గడిలో ఉన్న గుర్తు (0…9, #, +, !) ని బట్టి ఏం చెయ్యాలో (వేరే గుర్తు రాసి అటో ఇటో జరగడం) చెప్పాలి. అయ్యబాబోయ్, ఓ చిన్న కూడిక చెయ్యడానికి ఇంత ప్రయాసా అనుకోవచ్చు. కాని ఒక్కసారి ఆ పట్టిక తయారు చేస్తే చాలు, ఎంత పెద్ద కూడికనైనా యంత్రం చేసేస్తుంది.

సర్వతోముఖమైన ట్యూరింగ్ యంత్రం

ఒక్క గడి మీద ఒకే ఒక్క గుర్తు మీద పనిచెయ్యడం ముందర మరీ కట్టేసినట్లనిపించినా, కొన్ని చిన్న యంత్రాలు చేసేటప్పటికి అలవాటయి మెళకువలు తెలిసి సులువవుతుంది. మనం కాపీ యంత్రాన్ని వాడుకొని హెచ్చవేతల యంత్రాన్ని ఎలా చేశామో, అలాగే కొన్ని సరైన చిన్న చిన్న యంత్రాలని కలిపి ఎంతో క్లిష్టమైన సమస్యలని సాధించవచ్చు. అప్పుడు ఇది ఎంత శక్తివంతమైనదో తెలిసొస్తుంది. కూడికలూ, హెచ్చవేతలూ లాంటి చిన్న చిన్న లెక్కలే కాదు, వర్గాలు, వర్గ మూలాలు, వాటితో కూడిన పెద్ద పెద్ద సమాసాలు, కావలసినన్ని దశాంశ స్థానాల దాకా π విలువ, ఇలా మీకు తెలిసిన లెక్కలన్నీ ఈ యంత్రం చేత చేయించవచ్చు.

(π విలువ 22/7 అని మనం చిన్నప్పుడు చదువుకున్నాం. కాని అది ఉజ్జాయింపుగా ఇచ్చే విలువ. 22/7=3.1428571 1428571… అలా అంకెలు ఓ క్రమ పద్ధతిలో తిరిగి వస్తాయి. కాని π కరణీయ (irrational) సంఖ్య, దానిని రెండు సహజ సంఖ్యల నిష్పత్తిగా రాయలేము. దాని విలువ 3.14159265358979323846264338327950288419716939937510… అనంతంగా క్రమం లేకుండా ఉంటుంది.)

ట్యూరింగ్ తన పేపర్లో క్లిష్టమైన లెక్కలని చేసే యంత్రాలని చూపి, చివరకి, స్పష్టంగా వివరించిన పని – యాంత్రికంగా చేసే కంప్యుటేషన్ ఆల్గరిదమ్, (ఉదా: గ.సా.భ.) ఏదైనా సరే ట్యూరింగ్ యంత్రం చెయ్యగలదు అని తేల్చాడు. ట్యూరింగ్ యంత్రం చెయ్యలేని సమస్య ఉంటే, ఆ సమస్యకి ఆల్గరిదమ్ లేనట్లేనన్నాడు.

హిల్బర్ట్ ఏ గణిత సమస్యనైనా సరే నిరూపించగలమో లేదో చెప్పే ఆల్గరిదమ్ ఉందా అని అడిగాడు. ట్యూరింగ్ యంత్రం సాధించలేని సమస్య ఒక్కటున్నా సరే, హిల్బర్ట్ ప్రశ్నకి లేదు, అలాంటి ఆల్గరిదమ్ లేదు అని తేల్చి చెప్పవచ్చు.

హిల్బర్ట్ నిర్ణయ సమస్య అసాధ్యం

ఏ ట్యూరింగ్ యంత్రాన్నయినా తీసుకోండి. టేపు మీద ఓ సంఖ్యనిచ్చి, ఆ సంఖ్య మొదటి అంకె మీద యంత్రాన్ని మొదలు పెడితే ఆ యంత్రం పట్టిక ప్రకారం గడుల మీద కదులుతుంది. కొన్ని సంఖ్యలకి యంత్రం చివరకి ఆగి పోతుంది. మరికొన్నిటికి యంత్రం ఎప్పటికీ ఆగదు. ఏ సంఖ్యల మీదయితే యంత్రం చివరకి ఆగుతుందో, ఆ సంఖ్యలన్నిటినీ ఒక యంత్రపు ‘ఆగే సమితి’గా (halting set) గుర్తిద్దాం.

గోడెల్ అసంపూర్ణ సిద్ధాంతాలలో వాడిన సంకేత పద్దతిని (encoding technique) గుర్తు తెచ్చుకుందాం. ప్రతి గుర్తుకీ ఓ సంఖ్యనిచ్చాడు. ఫార్ములాలో గుర్తులన్నిటికీ కలిపి తమ తమ సంఖ్యల మూలంగా వచ్చే మరో సంఖ్యనిచ్చాడు. ఏ సిద్ధాంత నిరూపణ అయినా వరుసగా వున్న అనేక ఫార్ములాలే కాబట్టి, ఆ ఫార్ములాల సంఖ్యలతో నిరూపణకి మరో సంకేత సంఖ్యనిచ్చాడు. దీంట్లో ముఖ్యంగా గ్రహించవలసిందేమిటంటే, ఓ సిద్ధాంత సంకేత సంఖ్యనిస్తే మనం దాని నిరూపణ లోని ఫార్ములాలని సులభంగా రాబట్టవచ్చు. ఇలా గణిత ప్రతిపాదనల్ని సంఖ్యలుగా మార్చి, ఓ ప్రతిపాదనని నిరూపించగలమా అనేదానికీ దాని సంకేత సంఖ్య స్వభావం (సరి సంఖ్య, ప్రధాన సంఖ్య, లాంటి గుణాలు) గురించి అడిగే ప్రశ్నకీ లంకె పెట్టాడు. ట్యూరింగ్ కూడా ఇదే పద్ధతిని అవలంబించాడు – యంత్రానికి ఓ సంఖ్యనిచ్చి, ఆ సంఖ్య స్వభావానికీ యంత్ర స్వభావానికీ లంకె పెట్టాడు.

ఎలా? ట్యూరింగ్ యంత్రం అంటే కేవలం దాని కదలికలని వర్ణించే ఐదుపాళ్ళ అంశలున్న పట్టికేనని తెలుసుకున్నాం. గోడెల్ ఓ రుజువుని ఓ క్రమమైన వరుసలో ఉన్న ఫార్ములాలుగా చూసినట్లే, ట్యూరింగ్ యంత్రాన్ని ఓ వరుసలో ఉన్న ఐదుపాళ్ళ అంశలుగా చూడవచ్చు. ఉదాహరణకి, మనం పైన తెలుసుకున్న కూడిక యంత్రం లోని ఐదుపాళ్ళని, సెమికోలన్‌లతో విడదీస్తూ ఇలా రాయవచ్చు:

(S1, #, #, S1, R) ; (S1, 1, #, S2, R) ; (S2, #, 1, S3, R) ; (S2, 1, 1, S2, R)

సంకేత పద్ధతి:

• స్థితులు 9 తో మొదలై 9 తో ముగుస్తాయి: S1 = 919, S2 = 929, …, S8 = 989, S9 = 9119, S10 = 9129 …
• గుర్తులు 8 తో మొదలై 8 తో ముగుస్తాయి: 0 = 8008, 5 = 8058, 6 = 8518, 9 = 8548, # = 8558.
• కదలికలు 6 తో మొదలై 6 తో ముగుస్తాయి: L = 616, R = 626, N = 636.
• ; = 77

వరుసలో ఉన్న ఐదుపాళ్ళ అంశలని ఈ సంకేత పద్ధతి ద్వారా పేరిస్తే, ఓ పెద్ద సంఖ్య వస్తుంది. ఉదాహరణకి, పై కూడిక యంత్రం యొక్క సంకేత సంఖ్య:

919 8558 8558 919 626 77 919 8018 8558 929 626 77 929 8558 8018 939 626 77 929 8018 8018 929 626

చదవడానికి వీలుగా మధ్యలో ఖాళీ వదిలాను. అంత చిన్న యంత్రానికి ఇంత పెద్ద సంఖ్యా అని నిరుత్సాహపడకండి. మీరు దీనినేం గుర్తుంచుకోనవసరం లేదు. తెలుసుకోవాల్సిందేమిటంటే, ఈ పెద్ద సంఖ్య నుండి, మనం ఆ ట్యూరింగ్ యంత్రం ఐదుపాళ్ళ అంశలని రాబట్టవచ్చు: 77 అన్నది ఐదుపాళ్ళ అంశలని వేరుపరుస్తుంది కనుక సులభంగా ప్రతి ఐదుపాళ్ళ అంకెల వరుస సులభంగా తెలుసుకోవచ్చు. దాని నుండి, స్థితులూ, గుర్తులూ, కదలిక తేలిగ్గా రాబట్టవచ్చు.

అసలు మనం ట్యూరింగ్ యంత్రాన్ని దాని సంకేత సంఖ్యతో పిలవచ్చు.

ఇంతకు మునుపటి వ్యాసాలలో కేంటర్ (Cantor) అనంతాల గురించి కొన్ని ఆశ్చర్యకరమైన విషయాలు కనుగొన్నాడని తెలుసుకున్నాం: ఎన్నిసహజ సంఖ్యలున్నాయో (0, 1, 2, 3, …) అన్నే సరి సంఖ్యలున్నాయి (2, 4, 6, 8, …); భిన్న సంఖ్యలు (ratios or rational numbers) సహజ సంఖ్యలకన్నా ఎక్కువ లేవు. 0 కీ 1 కీ మధ్యనున్న భిన్నాలన్నిటినీ ఇలా వరుసగా వ్రాయవచ్చు:

1/2 1/3 1/4 2/3 1/5 1/6 2/5 3/4 1/7 3/7 1/8 …

(లవ హారాలని కూడితే ఇవి ఓ క్రమవరుసలో ఉన్నాయని తెలుస్తుంది.)

తన మూల పద్ధతి (diagonal method) అన్న కిటుకు ద్వారా 0 కీ 1 కీ మధ్య పై భిన్నాలకి చెందని సంఖ్యలున్నాయని కేంటర్ నిరూపించాడు. ఎలా? పై భిన్నాలని దశాంశ రూపంలో వరుసగా పట్టికలో వ్రాయండి:

1. .5000000000000…
2. .3333333333333…
3. .2500000000000…
4. .6666666666666…
5. .2000000000000…
6. …

మూలనున్న అంకెలతో కలిపి చేసిన సంఖ్య: .53060…

దాంట్లో ప్రతి అంకెనీ ఇలా మార్చండి: 0 నుండి 8 దాకా ఉన్న అంకెలకి ఒకటి కలపండి, 9 ని 0 చెయ్యండి. అప్పుడు వచ్చే సంఖ్య .64171…

ఈ కొత్త సంఖ్య పై సంఖ్యల్లో దేనికీ సమానం కాలేదు – కనీసం ఒక అంకెలోనన్నా తేడా ఉంటుంది కనుక. అంటే ఇది అకరణీయ (rational) సంఖ్యల్లో లేదు; ఇది వేరే రకమైన సంఖ్య, కరణీయ (irrational) సంఖ్య.

అలా కేంటర్ అకరణీయ సంఖ్య నుండి కరణీయ సంఖ్య ఎలా రాబట్టాడో, ట్యూరింగ్ కూడ పరికలన (computable) నుండి విపరికలన (uncomputable) సంఖ్యలుంటాయని చూపెట్టాడు. అదెలాగో ఇప్పుడు చూద్దాం.

ట్యూరింగ్ యంత్రాలన్నిటినీ ఓ క్రమ వరుసలో అమర్చుదాం. క్రింది పట్టికలో మొదటి నిలువ వరుసలో ట్యూరింగ్ యంత్రాలని – T1, T2, … అని రాశాను. మొదటి అడ్డు వరుసలో వాటి సంకేత సంఖ్యలని – T1 సంకేత సంఖ్య, T2 సంకేత సంఖ్య, … అనే పేర్లతో ఇచ్చాను. ఇప్పుడు, ప్రతి యంత్రం వరుసలోని గడులని ఆ యంత్రం వివిధ యంత్రాల సంకేత సంఖ్య మీద ఆగుతుందా లేదా అనే ప్రశ్నకి వచ్చే సమాధానంతో పూరిద్దాం. T1 తన సంకేత సంఖ్య మీదా T4 సంకేత సంఖ్య మీదా ఆగుతుంది కాని T2, T3 సంకేత సంఖ్యల మీద ఆగదు:

Ti యంత్రం Tj సంకేత సంఖ్య మీద ఆగుతుందా?

యంత్రం/ సంకేతసంఖ్య	T1 సంకేత సంఖ్య	T2 సంకేత సంఖ్య	T3 సంకేత సంఖ్య	T4 సంకేత సంఖ్య	…
T1	ఆగుతుంది	ఆగదు	ఆగదు	ఆగుతుంది	…
T2	ఆగదు	ఆగదు	ఆగుతుంది	ఆగదు	…
T3	ఆగదు	ఆగుతుంది	ఆగదు	ఆగుతుంది	…
T4	ఆగుతుంది	ఆగుతుంది	ఆగుతుంది	ఆగదు	…
…	…	…	…	…	…

ఇప్పుడు ఒక మూల నుండి మరో మూలకు వున్న సమాధానాల్ని చూడండి. వాటిని బట్టి ఓ కొత్త సమితి D ని ఇలా నిర్వచిద్దాం: దాంట్లో వుండేవన్నీ ట్యూరింగ్ యంత్రాల సంకేత సంఖ్యలే. కాని ఓ ట్యూరింగ్ యంత్రం తన సంకేత సంఖ్య మీద తను ఆగకపోతే మాత్రమే దాని సంకేత సంఖ్య ఈ సమితిలో వుంటుంది, ఆగితే వుండదు.

పై పట్టిక ప్రకారం, ఈ సమితిలో, T2, T3, T4 ల సంకేత సంఖ్యలు ఉంటాయి (ఆయా యంత్రాలు తమ సంకేత సంఖ్యపై ఆగవు కనుక), T1 సంకేత సంఖ్య ఉండదు (ఆ యంత్రం తన సంకేత సంఖ్యపై ఆగుతుంది కనుక).

ఏ ట్యూరింగ్ యంత్రపు సంఖ్య అయినా ఆ యంత్రపు ఆగే సమితికి చెందితే, ఆ సంఖ్య D కి చెందదు. ఆగే సమితికి చెందకపోతే, ఆ సంఖ్య D కి చెందుతుంది. దీని పర్యవసానం: D ఏ యంత్రపు ఆగే సమితికీ సమానం కాదు.

దీనికీ హిల్బర్ట్ నిర్ణయ సమస్యకీ ఏమిటి సంబంధం? గణితంలో ఏ ప్రశ్న వేసినా దానికి జవాబిచ్చే ఆల్గరిదమ్ ఉందా? అన్నది హిల్బర్ట్ ప్రశ్న. అది సమాధానం ఇవ్వలేని ప్రశ్న ఒక్కటున్నా సరే, హిల్బర్ట్ నిర్ణయ సమస్యకి పరిష్కారం లేనట్లే. అలాంటి ప్రశ్న ఒకటి ట్యూరింగ్ వేశాడు: ఏదైనా సంఖ్య ఇస్తే అది D సమితిలో ఉందా లేదా?

దీనికి ఆల్గరిదమ్ లేదు. ఎందుకు లేదో ఇలా రుజువు చేద్దాం: ఆల్గరిదమ్ ఉంది అని మొదలెట్టి అది ఓ వైరుధ్యానికి దారితీస్తుందని చూపెడదాం.

ఆల్గరిదమ్ ఏదన్నా ఉంటే, దానికి మనం ఓ ట్యూరింగ్ యంత్రాన్ని ఇవ్వగలగాలి. అంటే, స్థితులూ, కదలికలూ నిర్వచించే పట్టికనివ్వాలి. ఆ యంత్రానికి ఏదైనా సంఖ్యనిస్తే, ఆ సంఖ్య D సమితిలో ఉంటే టేపు మీద 1, లేకపోతే 0, రాసి ఆగాలి. అలా ఆగినప్పడు యంత్రం స్థితి Sf అనుకుందాం.

ఆ మొదటి యంత్రానికి రెండు ఐదుపాళ్ళ అంశలని చేర్చి కొత్త యంత్రాన్ని చేద్దాం: (Sf, 0, #, Sf, R), (Sf, #, #, Sf, R).

ఇచ్చిన సంఖ్య D సమితిలో ఉంటే ఈ కొత్త యంత్రం మొదటి యంత్రం లాగానే 1 రాసి ఆగుతుంది. లేకపోతే, ఈ యంత్రం ఎప్పటికీ ఆగదు. అంటే ఈ కొత్త యంత్రం మజిలీ సమితికీ, D సమితి కీ తేడా లేదు. కాని D సమితి ఏ ట్యూరింగ్ యంత్రం ఆగు సమితికీ సమానం కాదని కదా పైన నిర్వచించాం. ఈ వైరుధ్యానికి కారణం మనం పై ప్రశ్నకి ఆల్గరిదమ్ ఉందని అనుకోవడమే. అంటే ఆల్గరిదమ్ లేదు.

దీనిని హిల్బర్ట్ నిర్ణయ సమస్యతో ఎలా అన్వయించుకోవచ్చో చూద్దాం.

• ఆధార వాక్యం (Premise): ట్యూరింగ్ యంత్రం T టేపు మీద దాని సంకేత సంఖ్య n ఉంచాం.
• సిద్ధాంత వాక్యం (Conclusion): ఆ ట్యూరింగ్ యంత్రం అలా మొదలెడితే, చివరకు ఆగుతుంది.

పై ఆధార వాక్యం నుండి సిద్ధాంత వాక్యం నిరూపించగలమన్నా ఆ ట్యూరింగ్ యంత్రం ఆగుతుందన్నా ఒకటేనని ఫ్రెగె (Gottlob Frege) నియమాల ద్వారా చూపించవచ్చు. ఆ ట్యూరింగ్ యంత్రం ఆగుతుందనడం, n సంఖ్య D సమితిలో ఉందో లేదో తేల్చే ఆల్గరిదమ్ ఉందనడానికి సమానం. కాని అలాంటి ఆల్గరిదమ్ లేదని పైన నిరూపించాం. అంటే పై ఆధార వాక్యం నుండి సిద్ధాంత వాక్యం రాబట్టగలమో లేదో నిరూపించగలం అన్నది అవాస్తవం. నిరూపించలేని సమస్య ఒకటి చూపించాం కాబట్టి హిల్బర్ట్ సమస్యకి పరిష్కారం లేదు.

ట్యూరింగ్ సార్వత్రిక యంత్రం

పైన ఇచ్చిన రుజువుతో మనకెంత నమ్మకం ఉంది? ట్యూరింగ్ ఏమని చూపెట్టాడు? హిల్బర్ట్ సమస్యని సాధించే ట్యూరింగ్ యంత్రం అసాధ్యమన్నాడు. ట్యూరింగ్ యంత్రం కాకుండా మరేదైనా మార్గం ఉండవచ్చు గదా అన్న అనుమానం మనకు సహజంగానే రావచ్చు. అది చేసే పని మనం గణితం చేసేటప్పుడు చేసే ఆలోచన లాగే ఉన్నా, ఓ ప్రతిపాదనని వమ్ము చేసే రుజువులో దానికి అంత కీలకమైన పాత్ర ఇవ్వగలమా? మనకి నమ్మకం కలిగించడానికి, ట్యూరింగ్ తన పేపర్లో అనేక రకాలైన గణిత సూత్రాలని యంత్రంతో ఎలా సాధించవచ్చో చూపెట్టాడు. కాని వాటన్నంటి కన్నా అద్భుతమైనదొకటి కనిపెట్టాడు – ఏ ట్యూరింగ్ యంత్రం పనయినా చెయ్యగలిగే ట్యూరింగ్ సార్వత్రిక యంత్రం (Turing Universal Machine).

మనం ఇప్పటిదాకా ట్యూరింగ్ యంత్రం గురించి మాట్లాడినప్పుడు టేపు మీద దాని సాధకంతో (input)మొదలెట్టి చివరకి మిగిలేది ఉత్పాదకం (output) అన్నాము. యంత్రం ఒక స్థితి నుండి మరో స్థితికి పట్టిక ప్రకారం వెళ్తుందని అన్నాం. ఇప్పుడు, టేపు మీద, సాధకంతో పాటు ఆ యంత్రం సంకేత సంఖ్య కూడా పెడదాం:

Turing Machine M’s Code Number

Input X to M

…

దీనిని ఓ మనిషికిచ్చి, ఫలితం అడిగితే, ఏం చేస్తాడు? M సంకేత సంఖ్య నుండి దాని పట్టికని సులభంగా రాబట్టవచ్చని ముందరే తెలుసుకున్నాం. ఆ పట్టిక ప్రకారం M ఎలా పనిచేస్తుందో మనిషి కూడా, టేపు మీద, ప్రతి అడుగుకీ అచ్చం M పని చేసినట్లే యాంత్రికంగా చెయ్యవచ్చు. మరి యాంత్రికంగా చేసేదైతే మనిషే ఎందుకు? మరో ట్యూరింగ్ యంత్రాన్ని వాడితే పోలా అని ట్యూరింగ్ ఓ గొప్ప ఆలోచన చేశాడు. అదే సార్వత్రిక ట్యూరింగ్ యంత్రం (Universal Turing Machine). ఈ సార్వత్రిక ట్యూరింగ్ యంత్రం పనల్లా, వేరే ట్యూరింగ్ యంత్రం ఏ విధంగా పనిచేస్తుందో అచ్చు అలాగే పని చెయ్యడం.

ఈ సార్వత్రిక యంత్రం పట్టిక ఎలా ఉంటుంది? టేపు మీద ఏ భాగంలో తను అనుకరిస్తున్న యంత్రం సంకేత సంఖ్య ఉన్నదీ, ఏ భాగంలో దాని సాధకం ఉన్నదీ గుర్తు పెట్టుకోవాలి. సార్వత్రిక యంత్రం స్థితీ అనుకరిస్తున్న యంత్రం స్థితీ వేరుగా ఉండాలి. ట్యూరింగ్ ఈ అనుకరణ అంతా, జాగ్రత్తగా టేపు మీద సరైన గుర్తులు పెట్టుకుంటూ ఎలా చెయ్యవచ్చో పూర్తి పట్టిక ద్వారా చూపెట్టాడు. యంత్రం M, టేపు మీద X ఇస్తే ఫలితం ఏముంటుందో, యంత్రం U కూడా కచ్చితంగా అదే ఫలితాన్ని ఇస్తుందని నిరూపించాడు.

U యంత్రానికి M యంత్రం గురించి ముందే తెలియాల్సిన అవసరం లేదు. M సంకేత సంఖ్య (అంటే దాని పట్టిక) టేపు మీద ఓ భాగానికి పరిమితమై ఉండాలి. అంతే. వాడుకలో ఉన్న ఏ కంప్యూటర్ నైనా తీసుకోండి. మౌలికంగా దానికీ, ఇక్కడ చెప్పుకుంటున్న M యంత్రానికీ తేడా లేదు. ఆ కంప్యూటర్ పని చేసే విధానాన్ని పరిమితమైన స్థితులున్న పట్టిక ద్వారా నిర్వచించవచ్చు. అప్పుడు, సార్వత్రిక ట్యూరింగ్ యంత్రం, ఆ కంప్యూటర్ ని అనుకరించగలదు.

ఆగే సమస్య అసాధ్యం

ట్యూరింగ్ తన పేపర్లో ప్రస్తావించిన అసాధ్యమైన సమస్యలలో అతి ముఖ్యమైనది ఆగే సమస్య. మీలో కొందరు కంప్యూటర్ ప్రోగ్రాములు రాసి ఉంటారు. అప్పుడప్పుడు మీ ప్రోగ్రాము ఎంతకీ ఆగని సమయాలు (stuck in an infinite loop) ఉండి ఉంటాయి. దానిని డీబగ్ (debug) చేస్తూ మీరు రేయింబవళ్ళు కష్టపడి ఉండొచ్చు. ప్రోగ్రాము ఆగుతుందా లేదా అని చెప్పగలిగే సౌకర్యం ఉంటే ఎంత బావుండు అని మీరు ఆశపడి ఉండాలి. అలాంటి సౌకర్యం ఎందుకు లేదో, కాదు, అసలెప్పటికీ ఎందుకు ఉండదో చెప్తాను.

ఆ సమస్యని, ఈ సందర్భంలో ఇలా అడగవచ్చు: ఓ ట్యూరింగ్ యంత్రంతోపాటు దాని సాధకం ఇస్తే, ఆ యంత్రం ఆగుతుందో లేదో చెప్పగలమా? అంటే అది ఆగుతుందో లేదో చెప్పగలిగే ఆల్గరిదమ్ ఉన్నదా? ఆ ఆల్గరిదమ్ ఏదో ఒక ప్రత్యేకమైన ట్యూరింగ్ యంత్రమే కాదు, అసలే ట్యూరింగ్ యంత్రాన్నిచ్చినా అది ఆగుతుందో లేదో చెప్పాలి.

ఈ సమస్యకి సమాధానం – అలాంటి ఆల్గరిదమ్ అసాధ్యం. ఒక్కసారి ఆగి ఈ వాక్యం లోతు గ్రహించండి. రేఖాగణితంలో మనం వృత్తలేఖిని, రూళ్ళకర్ర మాత్రమే వాడి కోణాన్ని మూడు సమభాగాలు చెయ్యడం అసాధ్యం అని చదువుకున్నాం. కాని, ఆ పరిమితికి కారణం ఆ పనిముట్లు; ఇతర పనిముట్లతో త్రిఖండన సమస్యని సాధించవచ్చు. ఆగే సమస్య వేరు – మానవులీ సమస్యని సాధించే మార్గం ససేమిరా లేదు. దీని నిరూపణ నేనిక్కడ ఇవ్వడం లేదు గాని, ఇంతకు మునుపు లాగే సాధ్యము అనుకుంటే అదో వైరుధ్యానికి దారి తీస్తుందని చూపించవచ్చు.

ఇంతలో అట్లాంటిక్ అవతలి ఒడ్డున …

ఈ వివరాలన్నిటితోపాటు ముందు ముందు ఇంకా చెయ్యవలసిన పరిశోధన గురించి – అంతా ట్యూరింగ్ ఓ పెద్ద పేపరు రాసి, మొదటి డ్రాఫ్టు న్యూమన్‌కి 1936 ఏప్రిల్ మధ్యలో ఇచ్చాడు. న్యూమన్ వేరే పనులలో మునిగివుండి మరో వారం పది రోజుల్లో చదువుతానన్నాడు. మే నెల మధ్యలో ఆ పేపరు చదివి న్యూమన్ నివ్వెరపోయాడు. గోడెల్ సిద్ధాంతం వచ్చిన తర్వాత ఈ అయిదేళ్ళూ ఎంతో మంది మేధావులు తలమునకలవుతున్నారు. అంత సులభమైన యంత్రంతో హిల్బర్ట్ ప్రశ్నకి సమాధానం ఇవ్వొచ్చంటే నమ్మశక్యం కాలేదు. ట్యూరింగ్ ఊహ తప్పేమో, ట్యూరింగ్ యంత్రం సాధించలేని సమస్యని సాధించే మరికాస్త శక్తివంతమైన యంత్రం ఉందేమో, అని అనుమానం వచ్చింది. కాని చివరకి ట్యూరింగ్ యంత్రాన్ని అధిగమించే యంత్రం లేదని న్యూమన్ రూఢిపరచుకున్నాడు.

ఇంతలో అనూహ్యంగా అమెరికా నుండి ప్రచురితమయ్యే గణితశాస్త్ర పత్రిక (American Journal of Mathematics) సంచిక న్యూమన్‌కి చేరింది. దాంట్లో, ప్రిన్స్‌టన్ విశ్వవిద్యాలయంలో పనిచేస్తున్న ప్రొఫెసర్ చర్చ్ (Alonzo Church) రాసిన An Unsolvable Problem of Elementary Number Theory, అన్న పేపరు ఉంది. అది 1936 ఏప్రిల్ 15న ప్రచురితమయింది. ఇద్దరు గణితవేత్తలూ దాదాపు ఒకే సమయంలో హిల్బర్ట్ సమస్యకి పరిష్కారం లేదని కనుక్కున్నారు. ట్యూరింగ్ పేపరు ఇంకా డ్రాఫ్టు రూపంలోనే ఉన్నది. ప్రతిష్ఠాత్మక పత్రికలలో కొత్తగా కనుక్కున్న విషయలకే ప్రాముఖ్యత ఇస్తారు కావున ట్యూరింగ్ పేపరు ప్రచురణ అపాయంలో పడింది. కాని చర్చ్, ట్యూరింగ్‌ల మార్గాలు చాలా వేరు వేరు. ట్యూరింగ్ నిరూపించిన తీరుకీ చర్చ్ నిరూపించిన తీరుకీ పోలిక లేదు. గణితంలో యంత్రాల గురించిన ప్రస్తావనే ఉండదు కావున ట్యూరింగ్ మార్గం వినూత్నమైనది. అందువలన దానిని ప్రచురించాలని న్యూమన్ లండన్ మేథమేటికల్ సొసైటీకి సిఫార్సు చేశాడు.

అంతే కాక, మరీ స్వతంత్రంగా ఒంటరిగా పనిచేసే ట్యూరింగ్ అమెరికా వెళ్ళి కొన్నాళ్ళు చర్చ్తో పనిచేస్తే పరిశోధనలో లోటుపాట్లు తెలుస్తాయని భావించి, చర్చ్‌కి న్యూమన్ ఉత్తరం రాసి ఖర్చులకి కొంత స్కాలర్షిప్ వచ్చేటట్లు చూడమని కోరాడు. ప్రిన్స్‌టన్ వాళ్ళు ట్యూరింగ్‌ని రమ్మని ఆహ్వానించారు కాని స్కాలర్షిప్ మాత్రం వేరొకరికి ఇచ్చారు. అయినా ట్యూరింగ్ అమెరికాకి ప్రయాణమయ్యాడు. అక్కడి విశేషాలు వచ్చే వ్యాసంలో చూద్దాం.

నేనీ వ్యాసం రాయడానికి ఉపయోగించుకున్న పుస్తకాలు:

1. “కొడవటిగంటి కుటుంబరావు రచనా ప్రపంచం, పదవ సంపుటం – సైన్సు వ్యాసాలు,” విరసం ప్రచురణ, 2011.
2. “వంటలు – పిండి వంటలు,” మాలతీ చందూర్, క్వాలిటీ పబ్లిషర్స్, 1985.
3. “On Computable Numbers, with an Application to the ENTSCHEIDUNGSPROBLEM,” by A. M. Turing. Proceedings of the London Mathematical Society, November 30, 1936. ఇది ట్యూరింగ్ అసలు పేపరు. దీనిని ఆకళింపు చేసుకోవడం సులభం కాదు.
4. “The Annotated Turing: A Guided Tour through Alan Turing’s Historic Paper on Computability and the Turing Machine,” by Charles Petzold. Wiley Publishing, Inc. 2008. ట్యూరింగ్ పేపర్ని సామాన్య పాఠకులు అర్థం చేసుకోడానికి వీలుగా వివరణలు, సందర్భ సమాచారం తో కూడిన మంచి పుస్తకం.
5. “computers Ltd.: what they really can’t do,” by David Harel. Oxford University Press, 2000. దశాంశ పద్ధతిలో కూడిక చేసే ట్యూరింగ్ యంత్రాన్ని ఇక్కడ నుంచి తీసుకున్నాను.
6. “The Universal Computer: The Road from Leibnitz to Turing,” by Martin Davis. Turing Centenary Edition. CRC Press, 2011. ఈ వ్యాస పరంపరలో ఎక్కువ భాగం Davis పుస్తకం నుంచి తీసుకున్నాను. అందరూ చదవాల్సిన పుస్తకం.
7. “Alan Turing: The Enigma,” by Andrew Hodges. Princeton University Press, 2012 Centenary edition. ఇది ట్యూరింగ్ సాధికారిక జీవితచరిత్ర. Hodges పేరున్న గణితవేత్త, Oxford University లో ప్రొఫెసరు.
8. “The Man Who Knew Too Much: Alan Turing and the Invention of the Computer,” by David Leavitt. W. W. Norton & Company, 2006. ట్యూరింగ్ జీవిత చరిత్ర. Hodges ఉద్గ్రంథం చదవడానికి సమయం లేని వాళ్ళు దీనిని చదవచ్చు. ట్యూరింగ్ యంత్రాల వివరాలు బాగా ఉన్నాయి.
9. “Alan M. Turing,” by Sara Turing. Cambridge University Press, Centenary Edition, 2012. ట్యూరింగ్ చనిపొయిన కొద్ది సంవత్సరాలకే అతనికి రావలసిన గుర్తింపు రాలేదనీ, అతని జీవితం గురించీ, సైన్సు పరిశోధనల గురించీ ఇతరులు తెలుసుకోవాలనీ వాళ్ళమ్మ రాసిన జీవిత చరిత్ర. ట్యూరింగ్ చిన్నప్పటి వెర్రి చేష్టలతో పాటు, జీనియస్ అనిపించిన సందర్భాలతో పాటు ఆ కుటుంబం మనదేశంలో గడిపిన వివరాలు ఆసక్తికరమైనవి ఉన్నాయి. మొదట్లో కొద్ది కాపీలు మాత్రమే ప్రచురించారు. ఈ మధ్యనే ట్యూరింగ్ శత జయంతి సందర్భంగా తిరిగి ప్రచురించి మేలు చేశారు. సేరా ట్యూరింగ్ తన కొడుకు యాక్సిడెంటల్‌గా చనిపోయాడనే గాని ఆత్మహత్య మూలంగా కాదని నమ్ముతుంది. అతని అన్న దీనికి చివరిమాట వ్రాశాడు. న్యూమన్ భార్య ఓ ముందుమాట వ్రాసింది. Martin Davis వ్రాసిన ముందు మాట చెప్పుకోదగ్గది.
10. “Turing Machines,” by John E. Hopcroft. Scientific American, 250:5 (1984), 86-98. ఇది చాలా చక్కని వ్యాసం. కాపీ యంత్రం, హెచ్చవేత యంత్రం పూర్తిగా దీంట్లోంచి తీసుకున్నవే. ఈయన 1986 Turing Award ని Robert Tarjan తో పంచుకున్నాడు. అమెరికాలో పెద్ద పెద్ద శాస్త్రవేత్తలు కూడా సామాన్య పాఠకులకి శాస్త్రవిజ్ఞానం అందజెయ్యడానికి తపనపడతారనడానికి ఇదో మంచి ఉదాహరణ.
11. “What is a Computation?” by Martin Davis in “Mathematics Today – Twelve Informal Essays,” Edited by Lynn Arthur Steen. Springer-Verlag, 1978. జిజ్ఞాసగల వివేకవంతులైన సామాన్య పాఠకులకి గణితంలో జరుగుతున్న పరిశోధనల గురించి కొందరు ప్రముఖ గణితవేత్తలు రాసిన వ్యాసాలు. Davis వ్యాసంలో ఆగే సమస్య అసాధ్య నిరూపణతో పాటు మరికొన్ని ఆసక్తికరమైన విషయాలు ఉన్నాయి.