సంగ్రహము

ప్రాచీన భారతీయ గణితశాస్త్రములో కనుగొనబడిన విశేషాలలో కొన్ని ఛందశ్శాస్త్ర మార్గములో మనకు లభించినవి. యుగ్మాంకగణితము (binary arithmetic), ద్విపద సిద్ధాంతము (binomial theorem), మేరు నిర్మాణము (Pascal triangle), విరహాంక సంఖ్యలు (Fibonacci numbers) పింగళ, హలాయుధ, విరహాంక, గోపాల, హేమచంద్రాదుల అధ్యయన ఫలితమే. షట్ప్రత్యయాలీ సిద్ధాంతముల అంశములను వివరిస్తాయి. అనంతామాత్యుడు ఛందోదర్పణములో వీటిని చక్కగా విశదీకరిస్తాడు. మాత్రాఛందస్సు గురించి ప్రాకృత హిందీ భాషలలో నెక్కువగా వ్రాయబడియున్నను తెలుగులో వీటి చర్చ చాల పరిమితమే. కన్నడ తెలుగు భాషలలోని దేశి ఛందస్సులో అంశ లేక ఉపగణములను ఉపయోగిస్తారు. తెలుగులోని సూర్యేంద్రచంద్రగణములు కన్నడమునందలి బ్రహ్మ విష్ణు రుద్ర గణములనుండి పుట్టినవే. కాని వీటియొక్క మేరునిర్మాణమును గురించిన వ్యాఖ్యలు లేవు. వీటి మేరునిర్మాణము ఇక్కడ ప్రప్రథమముగా చర్చించదలిచాను. అంతే కాదు, యీ సిద్ధాంతమును సార్వత్రీకరించి క్రొత్త క్రొత్త గణములను, ఛందస్సును సృష్టించుటకు వీలగునని నిరూపించడానికి ప్రయత్నించాను.

పరిచయము

భారతీయ గణితశాస్త్రములో కొన్ని నూతనాంశములు ఛందశ్శాస్త్రము ద్వారా వెలుగులోనికి వచ్చాయి. నేడు మనము కంప్యూటరులలో ఉపయోగించే యుగ్మగణిత (binary arithmetic) సిద్ధాంతములు, పరిక్రియలు రెండు వేల సంవత్సరములకు ముందు వాడుకలో నున్నవే. నేడు మనము ఫిబనాచ్చీ శ్రేణి అని పిలిచే సంఖ్యలు సుమారు ఆఱవ శతాబ్దములో భారతదేశములో కనుగొనబడ్డాయి. అక్షర గణములు, మాత్రా గణములు, వీటితో నిర్మించబడిన అక్షర వృత్తములు, మాత్రా వృత్తములు అన్ని భాషలలో కవులచే ఉపయోగించబడినవే. ఇవిగాక కన్నడ తెలుగు భాషలలో అంశ లేక ఉపగణములచే అమర్చబడిన అక్కఱ, ద్విపద, రగడలాటి జాతి పద్యములు, సీసము, ఆటవెలది, తేటగీతివంటి ఉపజాతులకు చెందిన పద్యములు దేశి ఛందస్సు ప్రత్యేకత. ఈ వ్యాసపు ముఖ్యోద్దేశము యీ గణితాంశములపై మనకు ఇంతవఱకు పరిచితమైన విషయాల విశేషాలను తెలుపుట. అంశ లేక ఉపగణములపై నేను కనుగొన్న కొన్ని క్రొత్త విషయాలను, వాటిని ఉత్పత్తి చేసే విధానమును కూడ వివరించ ప్రయత్నిస్తాను.

పద్యములు గణసముదాయములు. గణములు కొన్ని అక్షరములచే నిర్మింపబడినవి. భారతీయ ఛందశ్శాస్త్రములో మనము ఎదుర్కొనే గణములు – అక్షర గణములు, మాత్రా గణములు, అంశ లేక ఉపగణములు, తమిళ ఛందస్సులోని శీరులు. అక్షర గణములు తమిళము తప్ప దాదాపు అన్ని భారతీయ భాషలలో ఉన్నాయి. సంస్కృత ఛందస్సులో మూడు అక్షరములకన్న ఎక్కువగా ఉండే గణములు లేవు. ఈ గణములను వరుసగా మొదటి పట్టికలో చూడవచ్చు. వీటిని గుర్తించడానికి య-మా-తా-రా-జ-భా-న-స-ల-గం అనే ఒక కొండ గుర్తును ఉపయోగిస్తారు. మూడు మూడక్షరములుగా తీసుకొంటే, ఆ గణపు పేరు దానికి మొదట ఉంటుంది, ఉదా. మాతారా – మ-గణము. పై సూత్రమునకు బదులు జ-రా-య-మా-తా-భా-న-స-ల-గం అనే సూత్రమును కూడ వాడవచ్చునని ఒకటి ఉంది. గురువుకు 0, లఘువుకు 1 సంఖ్యను నియోగించినప్పుడు, ఈ గణములు యుగ్మ సంఖ్యలకు (binary numbers) అమరిక అవుతుంది. ప్రాచీన భారతీయ గణితశాస్త్రములో నేటిలా కాక కనిష్ఠ సంఖ్యను ఎడమవైపు, గరిష్ఠ సంఖ్యను కుడివైపు ఉంచుతారు. మూడింటికన్న ఎక్కువగా అక్షరములు ఉన్నప్పుడు, వాటిని ఈ మూడక్షరాల గణములతో వివరిస్తారు, ఉదా. UUIIU – త-ల-గ (తెలుగులో దీనిని త-వ అని కూడ అంటారు), UUIUI – త-గ-ల (తెలుగులో దీనిని త-హ అని కూడ అంటారు). ఈ మూడక్షరాల గణములనే రెండువేల సంవత్సరాలుగా లాక్షణికులు ఉపయోగిస్తున్నారు. ఒకరిద్దరు దీనికి భిన్నముగా గణములను వివరించియున్నారు (మొదటి పట్టిక), కాని ఇవి సర్వజనామోదమును పొందలేదు.

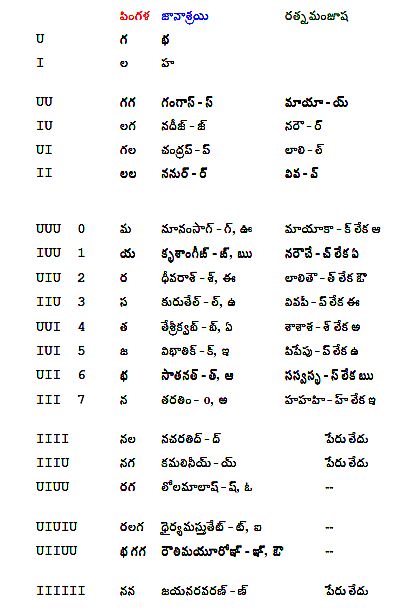
మొదటి పట్టిక – గణములు: ఇందులో U గురువుకు గుర్తు, I లఘువుకు గుర్తు. పింగళ ఛందస్సులోని గణములు ఎడమవైపు, జానాశ్రయిలో^[15] పేర్కొనబడిన గణములు మధ్య వరుసలో, రత్నమంజూషలో^[16] పేర్కొనబడిన గణములు కుడివైపు చూపబడ్డాయి. త్రిక గణములైన మ, భ, జ, స, న, య, ర, త లకు వాటి యుగ్మగణితాంకములు కూడ చూపబడ్డాయి. జానాశ్రయి కర్త గుణస్వామి సహాయముతో వ్రాసిన మాధవవర్మ (క్రీ. శ. 580-620) తాను పేర్కొన్న గణములకు హలంతములతో, అచ్చులతో పేర్లు పెట్టాడు. ఉదాహరణకు మ-గణమును గ్ అనియు లేక ఊ అనియు పేర్కొన్నాడు. అజ్ఞాతుడైన రత్నమంజూష రచయిత (ఇతడు హేమచంద్రునికన్న ముందున్న వాడు) అదే మ-గణమును క్ లేక ఆ అని పిలిచాడు.

షట్ప్రత్యయములు

ఛందశ్శాస్త్రములోని గణితాంశములను షట్ప్రత్యయములు నిరూపిస్తాయి. ప్రస్తారము, నష్టలబ్ధి, ఉద్దిష్టము, వృత్త సంఖ్య, లగ క్రియ, అధ్వము – ఈ ఆఱింటిని షట్ప్రత్యయములు అంటారు. అక్షరములు రెండు విధములు – గురువు, లఘువు. సంయుక్తాక్షరము ముందున్న అక్షరము, పొల్లుతో కూడిన అక్షరము (ఉదా. ద్రుతప్రకృతికము), బిందుయుక్త అక్షరము, ప్లుతము (సాగించి పలికే అక్షరములు) దీర్ఘాక్షరముతో కూడ గురుతుల్యమే. ఒక అక్షరము గురువుగానో లేక లఘువుగానో మాత్రమే పరిగణించబడుతుంది. ఈ షట్ప్రత్యయ వివరాలు చక్కగా అనంతామాత్యుని ఛందోదర్పణములో^[1,2] తెలుపబడ్డాయి.

వృత్త సంఖ్య

కొన్ని అక్షరముల (n) వృత్త పాదము ఒకటి ఉండినప్పుడు, అందులో ఎన్ని వృత్తములు జనింపగలవన్న మొదటి ప్రశ్న వృత్త సంఖ్య. దాని జవాబు – 2 ను 2 తో ఆ అక్షరముల సంఖ్య(n) యెంతో అన్ని సార్లు గుణించగా వచ్చే సంఖ్య, 2ⁿ. ఒక వృత్త పాదములో ఆఱు అక్షరములు ఉండినప్పుడు, మనకు 2.2.2.2.2.2 = 64 వృత్తములు, అనగా 2⁶ వృత్తములు లభిస్తాయి.

ప్రస్తారము

ఇక రెండవ ప్రశ్న – అందులో గురులఘువుల అమరికలు ఏలాగుంటాయి? దీనినే ప్రస్తారము అంటారు. దీనికి జవాబు ఆఱు అక్షరాల వృత్తాల పట్టికలో (రెండవ పట్టిక) చూడ వీలవుతుంది. మొదట అన్ని అక్షరములు గురువులుగా వ్రాయాలి. తరువాత రెండవ పంక్తిలో ఎడమవైపు గురువు క్రింద లఘువును ఉంచి కుడివైపు అక్షరములను అలాగే ఉంచి వ్రాయాలి. ఎడమవైపు లఘువులను గురువులుగా వ్రాయాలి. 6 అక్షరముల వృత్తములలో మొదటిది UUUUUU, రెండవది IUUUUU, మూడవది UIUUUU. ఇలాగే మనము గురులఘువులను మార్చుకొని వ్రాస్తూ వెళ్ళితే, చివరి వృత్తము IIIIII అవుతుంది. UUUUUU వృత్తపు యుగ్మాంకము 0, IIIIII వృత్తపు యుగ్మాంకము 63. వీటికి ఒకటి సంఖ్యను కూడిస్తే మనకు వృత్తపు సంఖ్య దొరుకుతుంది.

మూడవ, నాలుగవ ప్రశ్నలు – ఒక వృత్త సంఖ్యకు గురులఘువుల అమరిక, ఒక గురులఘువుల అమరికకు సరిపోయే వృత్త సంఖ్య ఏ విధముగా పొందుటకు వీలవుతుంది? మొదటి ప్రక్రియను నష్టలబ్ధి అని, రెండవ ప్రక్రియను ఉద్దిష్టము అని అంటారు.

నష్టలబ్ధి

వృత్త సంఖ్యనుండి ఒకటి తీసివేసినప్పుడు వచ్చిన సంఖ్యను యుగ్మాంకముగా వ్రాసి, అందులోని శూన్య సంఖ్యలను గురువుచే, ఏక సంఖ్యను లఘువుచే మార్చగా వచ్చే అమరిక ఆ వృత్తపు గురులఘువుల అమరికను తెలుపుతుంది. ఉదాహరణకు జగతీఛందములో 1171వ వృత్తపు గురులఘువుల అమరిక ఏలాగుంటుంది? 1171 సంఖ్యనుండి 1 తీసివేయగా 1170 మనకు లభిస్తుంది. దశాంశ సంఖ్య 1170 యొక్క యుగ్మాంకము 010010010010 కాబట్టి దీని గురు లఘువులు – UIUUIUUIUUIU, ఇది జగతీఛందములోని స్రగ్విణీ వృత్తము. దీనినే ఈ క్రింది విధముగా పొందవచ్చు: సంఖ్యను 2 అంకెతో విభజించి, అది బేసి సంఖ్య అయితే ఒకటి కలిపి మళ్ళీ ఒకటి సంఖ్య లభించువరకు విభజించాలి. ఎక్కడెక్కడ బేసి సంఖ్య వస్తుందో అక్కడ గురువును, మిగిలిన చోట లఘువును ఉంచితే ఆ వృత్తపు గురులఘువులు మనకు లభిస్తుంది. పై ఉదాహరణలో –

1171+1/2 = 586/2 = 293+1 = 294/2 = UIU

147+1 = 148/2 = 74/2 = 37+1 = 38/2 = UIU

19+1 = 20/2 = 10/2 = 5+1 = 6/2 = UIU

3+1 = 4/2 = 2/2 = 1+1 = 2/2 = 1 UIU

ఉద్దిష్టము

గురువులకు బదులు 0, లఘువులకు బదులు 1 సంఖ్యను ఉంచితే వచ్చిన యుగ్మాంకానికి సరిపోయే దశాంశ సంఖ్యకు ఒకటి చేరిస్తే ఆ గురులఘువుల అమరికకు సరిపోయే వృత్త సంఖ్య లభిస్తుంది. ఉదాహరణకు, పదవ ఛందములో రుక్మవతీవృత్తపు సంఖ్య ఏమి? రుక్మవతి గణములు UII UU UII UU. దీని యుగ్మాంకము 0110001100, అనగా దీని దశాంశ సంఖ్య 0+2+4+0+0+0+64+128+0+0 = 198. దీనికి ఒకటి చేరిస్తే వచ్చిన 199 రుక్మవతీ వృత్తపు సంఖ్య. ప్రతి పాదానికి పది అక్షరాలు ఉండే పంక్తి ఛందం ఈ వృత్తలక్షణం.

లగ క్రియ – ద్విపద సిద్ధాంతము

పాదానికి 26 అక్షరముల వఱకు ఉండే ఛందములలో ఒక ఛందములో ఎన్ని వృత్తములు పుట్టగలవు అని, వాటి ప్రస్తారము, అందులోని వృత్తపు అమరికలు, వాటి సంఖ్యలను గురించి మనము తెలుసుకొన్నాము. ఆ ఛందములోని వృత్తములలో ఒక గురువు గల వృత్తములు ఎన్ని, రెండు గురువులుగల వృత్తములు ఎన్ని, …, ఒక గురువు కూడ లేని వృత్తములు ఎన్ని మొదలగు ప్రశ్నలకు ఈ లగక్రియ జవాబు ఇస్తుంది. ఇది మనము సామాన్యముగా బీజగణితములో (Algebra లో) ద్విపద సిద్ధాంతము (Binomial theorem) అని వ్యవహరించబడే సిద్ధాంతపు మరో రూపము. అది:

(a+b)ⁿ = C(n,0) aⁿ b⁰ + C(n,1) a^n-1 b¹ + C(n,2) a^n-2 b² + … + C(n,n-1) a¹ b^n-1 + C(n,n) a⁰ bⁿ

where C(n,r) = n! / r! (n-r)! is the binomial coefficient for a^r b^n-r

a కు బదులుగా గురువు, b కు బదులుగా లఘువు, n కు బదులుగా ఆ ఛందములో ఉండే సమవృత్తపు పాదాక్షరముల సంఖ్యను ఉంచితే మనకు లభించే గుణకము (coefficient) అందులోని r గురువులు, n-r లఘువులు ఉండే వృత్తముల సంఖ్యను తెలుపుతుంది. ఉదాహరణకు, నాలుగవ ఛందములో గురువులు లేని (అంటే నాలుగు లఘువులు ఉండే) వృత్తము 1; 1 గురువు, 3 లఘువులు ఉండే వృత్తములు 4; 2 గురువులు, 2 లఘువులు ఉండే వృత్తములు 6; 3 గురువులు, 1 లఘువు ఉండే వృత్తములు 4; అన్నియు లఘువులుగా ఉండే వృత్తము 1. వృత్తముల మొత్తము 1+4+6+4+1 = 16 = 2⁴.

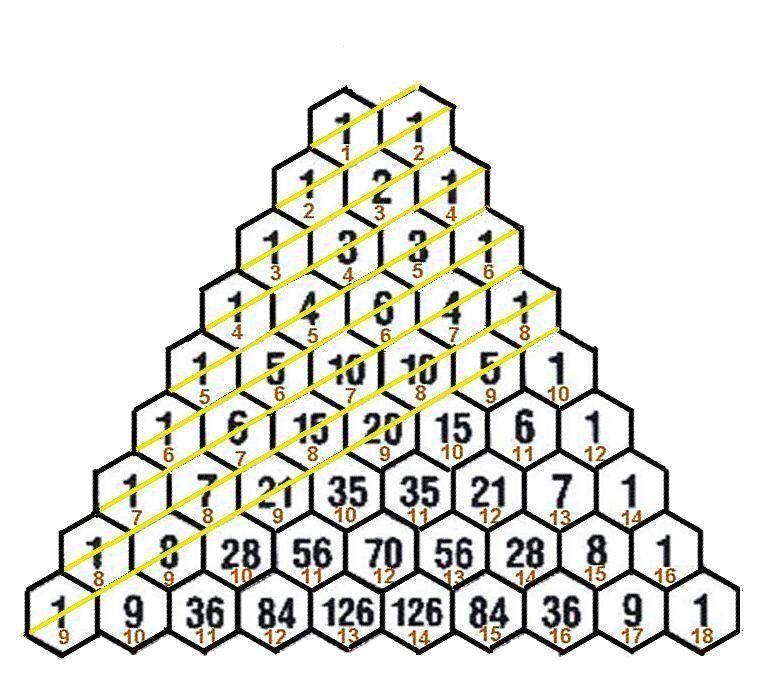
చిత్రము 1. అక్షరమేరువు. పాదమునకు 1 అక్షరము నుండి 9 అక్షరముల వఱకు ఉండే వృత్తములకు గురులఘువుల సంఖ్యల గుణకములు పెద్ద అచ్చు అంకెలతో చూపబడ్డాయి. ఉదాహరణకు ఆఱవ ఛందములో గురువులు లేని వృత్తము 1, 1 గురువు వృత్తములు 6, 2 గురువుల వృత్తములు 15, 3 గురువుల వృత్తములు 20, నాలుగు గురువుల వృత్తములు 15, ఐదు గురువుల వృత్తములు 6, అన్నీ గురువులుగా ఉండే వృత్తము 1. ఈ వృత్తములలోని మాత్రల సంఖ్య వరుసగా 6 నుండి 12. ఇవి చిన్న అచ్చులో చూపబడ్డాయి. ఒకే మాత్రా సంఖ్యతోటి వృత్తములు పసుపు గీతతో కలుపబడ్డాయి. వీటి కూడిక విరహాంకుని అంకెలవుతాయి.

ద్విపద సిద్ధాంతములో కనిపించే గుణకములను ఒక గోపుర రూపములో నిర్మించవచ్చు. దీనిని మేరు(వు) అంటారు. పర్వతాకారములో ఉంటుంది కాబట్టి దీనికి ఈ పేరు వచ్చింది. ఇది మొట్టమొదట హలాయుధవృత్తిలో^[3] వివరించబడ్డది. ఈ హలాయుధవృత్తి పదవ శతాబ్దపు హలాయుధుడు పింగళ ఛందస్సుకు వ్రాసిన టీక. త్రిభుజాకారములో నుండే ఈ (అక్షర)మేరువు నేడు 17వ శతాబ్దములో నివసించిన Pascal పేరితో Pascal triangle అని వ్యవహరించబడుతున్నది. నేను నిర్మించిన ఈ చిత్రములో మరికొన్ని విశేషాలను కూడ ఉన్నాయి:

(1) సామాన్యముగా మేరువులో చూపబడే ఒక గడి కలశమును చూపలేదు. ఎందుకంటే అది శూన్యాక్షర వృత్తమునకు సరిపోతుంది. కాని అక్షరములు లేక వృత్తములు లేవు గదా? అందువల్ల దానిని చూపలేదు.
(2) n అక్షరాలు ఉండే వృత్త పాదములో కనీసపు మాత్రల సంఖ్య n (అంటే అన్ని అక్షరాలు లఘువులు), ఎక్కువగా ఉండే మాత్రలు దీనికి రెట్టింపు, 2n. ఈ సంఖ్యలు ఎడమవైపు, కుడివైపు చిన్న అక్షరాలతో ఊదా రంగుతో చూపబడ్డాయి. మధ్యలో ఉండే గడులలో మిగిలిన మాత్రల సంఖ్యలను చూడవచ్చు. అంటే n అక్షరాలు ఉండే వృత్తానికి n, n+1, n+2, … , 2n మాత్రలు ఉంటాయి.
(3) ఈ మాత్రలు ఉండే వృత్తముల సంఖ్యలను (పెద్ద అచ్చు) లేత పసుపు రంగు గీతలతో కలిపితే మనకు 1, 2, 3, 5, 8, 13, 21, 34, 55, … మొదలైన సంఖ్యలు లభిస్తాయి. ఇవి విరహాంక సంఖ్యలు. వీటిని గురించిన విశేషాలను మాత్రాగణములను గురించి విశదీకరించేటప్పుడు చర్చిస్తాను.
(4) రెండు అడ్డ గడులలో ఉండే సంఖ్యల మొత్తము వాటికి క్రింద ఉండే గడిలో వ్రాయాలి.

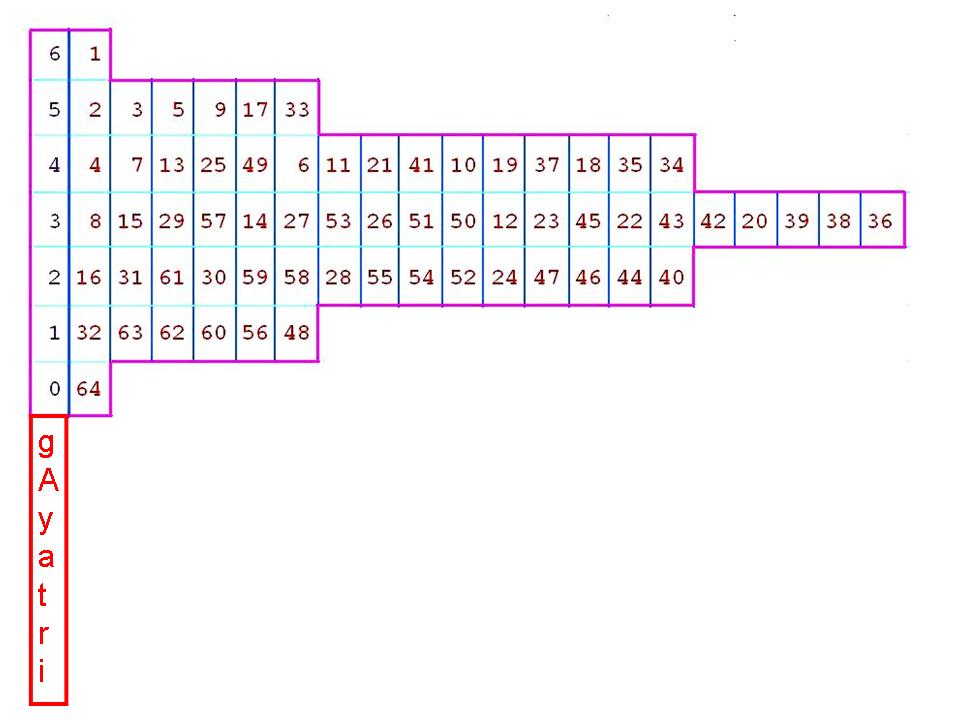
చిత్రము 2. గాయత్రీఛందపు పతాక. ఇందులో అన్ని గురువులు (6) గల వృత్తపు సంఖ్య పైన, అన్ని లఘువులు (6) కలిగి గురువు లేని వృత్తపు సంఖ్య క్రింద చూపబడ్డది. మిగిలిన వృత్త సంఖ్యలు ఆయా గురువుల సంఖ్యకు సరిపోతాయి.

అక్షరమేరు లేక లగక్రియ ఒక్కొక్క ఛందములో పుట్టిన వృత్తములో యెన్ని గురు లఘు వృత్తములో యన్న సంఖ్యను తెలుపుతుంది. ఒక్కొక్క ఛందములో పుట్టిన వృత్తములో యే యే వృత్తములో ఎన్ని గురువులు లేక లఘువులు ఉన్నాయో అన్న విషయమును తెలిపే పద్ధతిని సగణ లగక్రియ లేక పతాక అంటారు. ఆఱు అక్షరాలు ఉండే గాయత్రీ ఛందపు పతాకను రెండవ చిత్రములో చూడవచ్చు. అందులో ఊదా నిలువు గీతకు ముందు ఉండే అంకెలు గురువుల సంఖ్యను, ఎఱ్ఱటి రంగులో ఉండే సంఖ్యలు, వృత్తపు సంఖ్యను తెలుపుతాయి. ఉదాహరణకు, 2, 3, 5, 9, 17, 33వ వృత్తములకు ఐదు గురువులు, ఒక లఘువు ఉంటాయి. మొదటి నిలువు వరుసలో 2⁰=1 నుండి 2⁶=64 వరకు అంకెలు ఉంటాయి. మొదటి చిత్రాన్ని గమనిస్తే ఆఱు అక్షరాలు ఉండే వృత్తములో ఆఱు గురువులు ఉండే వృత్తము 1, ఐదు గురువుల వృత్తములు 6, నాలుగు గురువుల వృత్తములు 15, మూడు గురువుల వృత్తములు 20, రెండు గురువుల వృత్తములు 15, ఒక గురువు వృత్తములు 6, గురువులు లేని వృత్తము 1 అనే విషయము బోధపడుతుంది. పతాకలో మొదటి వరుసలో మొదటి వృత్తమునకు అన్నియు గురువులు. రెండవ వరుసలో ప్రతి సంఖ్యను రెట్టింపు చేసి ఒకటి తగ్గించగా వచ్చిన సంఖ్యలు ఇవ్వబడ్డాయి. ఆ సంఖ్య 64 కంటె ఎక్కువైతే పై వరుసలోని రెండవ సంఖ్యనుండి రెట్టింపు చేసిన సంఖ్యను వ్రాయవలసి వస్తుంది. ఈ సమాచారం సేకరించడానికి నేను ప్రత్యేకంగా కంప్యూటర్ ప్రోగ్రాములను వ్రాశాను. వాటి ద్వారా లభించిన కొన్ని ఫలితాలను కూడ రెండవ పట్టికలో చూడవచ్చు.

అధ్వప్రక్రియ

షట్ప్రత్యయాలలో చివరిది అధ్వప్రక్రియ. ఒక ఛందమునకు ప్రస్తారము చేయాలంటే ఎంత స్థలము కావాలన్న ప్రశ్నకు ఇది జవాబు నిస్తుంది. ఒక ఛందములో n అక్షరాలు ఉంటే, దాని ప్రస్తారానికి (2n-1) x (2^n-1) చదురపు అంగుళములు కావాలి. ఇందులో అక్షరాలకు మధ్య ఒక అంగుళపు జాగా కూడ ఉన్నది. అంగుళములకు బదులు మరే పరిమాణమునైనా మనము ఉపయోగించుకొనవచ్చు (ఉదా: అర్ధ సెంటీమీటరు).

మాత్రా ఛందస్సు

మాత్రా ఛందస్సులోని గణితాంశములను గురించిన విషయాలు తెలుగులో ఎక్కువగా లేవు. తెలుగులో మాత్రాఛందస్సుకు పరిమితమైన పద్యాలు కందము, రగడలు మాత్రమే. అందులో రగడలు ఉదాహరణ కావ్యాలలో, కొన్ని ప్రబంధ వర్ణనలలో మాత్రమే ఉపయోగించబడ్డాయి. సంస్కృతములోని ఆర్యాగీతి, ప్రాకృతములోని స్ఖందఅ కన్నడ తెలుగు భాషలలో కంద పద్యపు రూపు దాల్చింది. ఇందులో చతుర్మాత్రాగణములు ఉపయోగించబడ్డా, వాటికి కొన్ని ప్రత్యేక నియమా లున్నాయి. ఈ కారణాలవల్ల మాత్రాఛందస్సు వివరణ తెలుగు లక్షణ గ్రంథాలలో క్లుప్తంగా ఉంటుంది. కాని మాత్రాఛందస్సు ప్రాకృతములో, దాని ప్రభావం వలన ఉత్తర భారతీయ భాషలలో ఒక ప్రముఖ స్థానాన్ని ఆక్రమించుకొన్నది.

మాత్రాఛందస్సుకు, ఈ ఛందస్సుపై ఆధారపడిన తాళవృత్తాలకు ఒక విధముగా సుమారు 6-8 శతాబ్దముల మధ్య కాలములో నివసించిన విరహాంకుడు మూలపురుషుడని చెప్పవచ్చు. ఇతడు వ్రాసిన వృత్తజాతిసముచ్చయము అనే గ్రంథం చాలా ముఖ్యమైనది. ఇందులో మొట్ట మొదట నేడు ఫిబనాచ్చి శ్రేణి^{[4, 5]} అని పేరుపొందిన సంఖ్యలు మన కళ్ళకు అగపడుతాయి. ఈ సంఖ్యలు 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ఇత్యాదులు. ఈ అంకెల పంక్తిలో ముందున్న రెండు అంకెలను కూడిక చేసితే తరువాతిది వస్తుంది, ఉదా. 2+3=5, 34+55=89. ఈ ఫిబనాచ్చీ సంఖ్యలను మొట్టమొదట భారతీయులే కనుగొన్నారని పాశ్చాత్యులు^[6] కూడా అంగీకరించారు. ఛందశ్శాస్త్రములో ఈ అంకెలు ఎందుకు గోచరిస్తాయంటే – ఒక ప్రత్యేక సంఖ్య గల మాత్రలు ఉండే గణముల సంఖ్య ఈ సంఖ్యలలో ఒకటిగా ఉండాలి. ఒక మాత్ర ఉండే మాత్రాగణము 1, రెండు మాత్రలున్న మాత్రాగణములు 2, మూడు మాత్రలుండే మాత్రాగణములు 3, నాలుగు మాత్రలకు 5 గణములు, 5 మాత్రలకు 8 గణములు, ఇలా అన్ని మాత్రాగణముల సంఖ్య ఈ వరుసలో ఉండే సంఖ్యలకు మాత్రమే పరిమితము. విరహాంకుడు కనుగొన్న ఈ అంకెలు ఎక్కడెక్కడ పెరుగుదల (growth) ఉంటుందో, అక్కడక్కడ మనకు కనబడతాయి. అందుకే ఈ సంఖ్యలలోని సౌష్ఠవమును dynamic symmetry అంటారు. మాత్రాగణములలో మాత్రమే కాదు, సంగీత తాళప్రస్తారములో కూడ దీనికి ఒక స్థానము ఉన్నది.

ప్రస్తారము

ఈ మాత్రాగణముల ప్రస్తారము కూడ అక్షర గణముల ప్రస్తారము వంటిదే. ఏవో ఒకటి రెండు పుస్తకాలలో తప్ప ఇది కూడ తెలుగు ఛందోగ్రంథాలలో ఎక్కువగా వివరించబడలేదు. ఇందులో కూడ మొదటి గణము మాత్రల సంఖ్య సరి యయితే అన్ని గురువులతో, బేసి యయితే మొదట లఘువు, తరువాత గురువులతో ప్రారంభ మవుతుంది. తరువాత మొదటి గురువు క్రింద లఘువును ఉంచి, కుడి వైపు గురులఘువులను అలాగే ఉంచి ఎడమవైపు లఘువులను గురువు చేసి వ్రాయాలి. మరొక నియమము మాత్రల సంఖ్య మారకుండ చూసికోవాలి. ఒకటినుండి తొమ్మిది మాత్రలు ఉండే గణముల ప్రస్తారము మూడవ పట్టికలో చూపబడింది. ఇక్కడ ఒక విషయము గమనార్హం. ఈ గణములకు సరిపోయే దశాంశ సంఖ్య అక్షరగణ ప్రస్తారములో వరుసగా వస్తుంది, కాని మాత్రాగణ ప్రస్తారములో పెద్ద అంకె ముందు, చిన్న అంకె తరువాత కూడ వస్తుంది కొన్ని కొన్ని చోట్లలో. నా ఉద్దేశంలో ఇది ఒక పెద్ద భేదము.

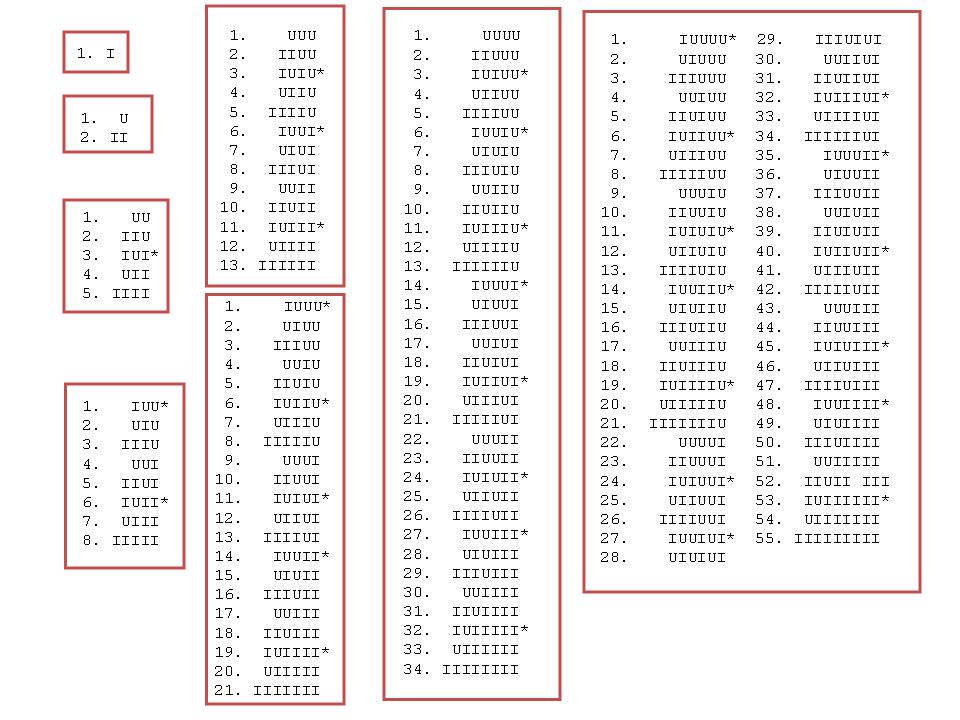
పట్టిక 3. మాత్రాగణోత్పత్తి: ఇందులో 1 నుండి 8 మాత్రలకు అందులో జనించిన వృత్తములు, వాటి సంఖ్యలు చూపబడ్డాయి. ఎదురు నడక గల వృత్తములు నక్షత్ర చిహ్నముతో చూపబడ్డాయి, వీటి సంఖ్యలు (1,1,2,3,5,8,13) కూడా విరహాంకుని అంకెలే.

వృత్త సంఖ్య

అక్షర వృత్తములలో ఏవిధంగా యుగ్మ గణితములోని రెండు అంకెయొక్క ఘాతమును (exponent) ఉపయోగిస్తామో, అదే విధంగా మాత్రాఛందస్సులో విరహాంకుని అంకెలను ఉపయోగిస్తాము. తొమ్మిది మాత్రలున్న వృత్తజాతిలో UUIUII అమరికతో ఉన్న వృత్తసంఖ్య యేమి?

(1) తొమ్మిది మాత్రలు ఉండే వృత్తముల మొత్త సంఖ్య 55. కాబట్టి వృత్త సంఖ్య 1 నుండి 55 వరకు గల సంఖ్యలలో ఒకటిగా ఉంటుంది.

(2) మొట్ట మొదట 1 నుండి 55 వరకు గల విరహాంక సంఖ్యలను క్రింది విధముగా వ్రాయాలి –

1 2 3 5 8 13 21 34 55

(3) మొదటి గురువును ఒకటి క్రింద వ్రాయాలి.

1 2 3 5 8 13 21 34 55
U

(4) గురువు వచ్చినప్పుడల్లా దాని తరువాతి సంఖ్య క్రింద ఏమీ వ్రాయకుండా తరువాత వచ్చే గురువునో లేక లఘువునో దాని తరువాతి అంకె క్రింద వ్రాయాలి. లఘువు వచ్చినప్పుడు ఈ నియమము లేదు. ఇలా వ్రాస్తే మనకు క్రింది అమరిక లభిస్తుంది –

1 2 3 5 8 13 21 34 55
U – U – I  U  –  I  I

(5) గురువుకు సరిపోయే విరహాంకుని అంకెలను కూడిక చేయాలి. అలా చేస్తే మనకు 17 వస్తుంది. దీనిని మొత్త వృత్తముల సంఖ్యనుండి తీసివేయగా వచ్చిన సంఖ్య వృత్త సంఖ్య. 55 నుండి 17 తీసివేస్తే మనకు 38 వస్తుంది. అది తొమ్మిది మాత్రలు ఉండే UUIUII వృత్తపు సంఖ్య.

గురులఘువుల అమరిక

అదే విధముగా మనకు తొమ్మిది మాత్రలు గల 45వ వృత్తపు గురులఘువులు కావలసినప్పుడు ఈ మార్గమును అనుసరించాలి.

(1) తొమ్మిది మాత్రలతో ఉండే వృత్తములు 55. అందులో 45ను తీసివేసినప్పుడు మనకు 10 లభిస్తుంది.

(2) తరువాత విరహాంకుని అంకెలను వరుసగా వ్రాసి, వాటి క్రింద లఘువులను ఉంచాలి.

1 2 3 5 8 13 21 34 55
I I I I I  I  I  I  I

(3) 10కన్న తక్కువ లేక సమానమైన సంఖ్య 8. అది తీసి వేస్తే మనకు రెండు మిగులుతుంది. 2కు తక్కువ లేక సమానమైన సంఖ్య 2. అది తీసి వేస్తే సున్న మిగుల్తుంది. ఈ అంకెలైన 8, 2 ల క్రింద లఘువుకు బదులు గురువును ఉంచాలి. అప్పుడు మనకు క్రింది అమరిక లభిస్తుంది –

1 2 3 5 8 13 21 34 55
I U I I U  I  I  I  I 

(4) ఇప్పుడు గురువు ప్రక్కన లఘువులుంటే, అందులోని మొదటి లఘువును తొలగించగా వచ్చిన అమరిక మనకు కావలసిన అమరిక అవుతుంది – IUIUIII, ఇందులో 2 గురువులు, 5 లఘువులు, మొత్తము తొమ్మిది మాత్రలు ఉన్నాయి.

మాత్రామేరువు

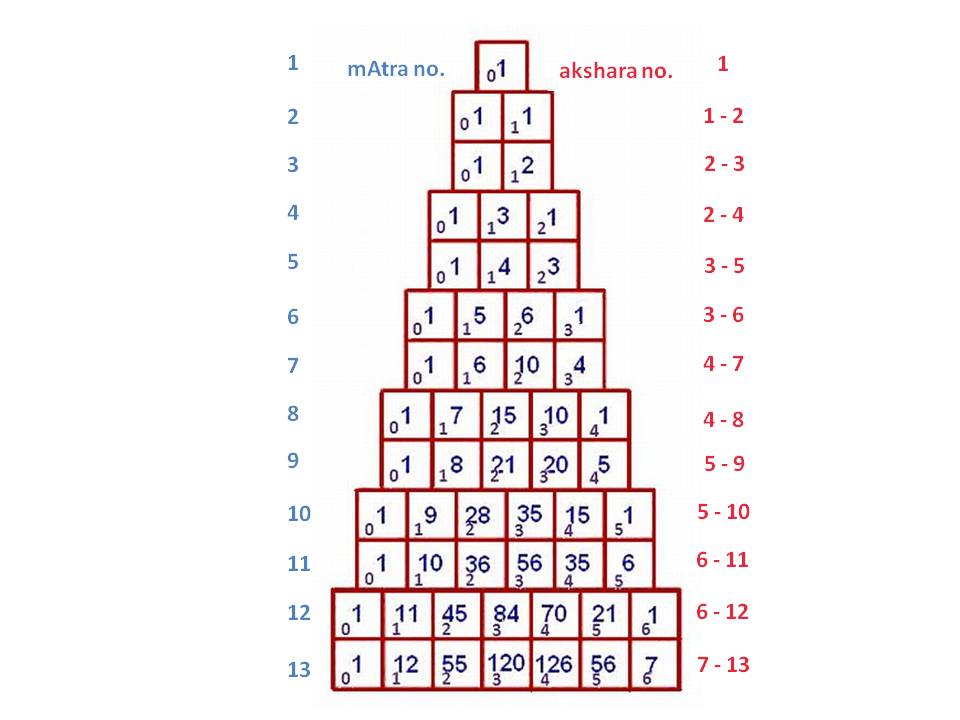
చిత్రము 3. మాత్రామేరువు. ఇందులో నిలువు వరుసలో మాత్రల సంఖ్య ఎడమవైపు (ఊదా రంగులో), అక్షరముల సంఖ్య కుడివైపు (ఎఱ్ఱటి రంగులో) చూపబడ్డాయి. చిన్న అచ్చులోని అంకెలు గురువుల సంఖ్యను, పెద్ద అచ్చులోని అంకెలు వృత్త సంఖ్యను సూచిస్తాయి.

అక్షర లేక వార్ణిక ఛందస్సులో మనము ఎదురుకొనే మేరువును మొదటి చిత్రములో చూశాము. అందులో లేత రంగు గీతలతో కొన్ని అంకెలను కలిపియున్నాను. ఆ అంకెలే మాత్రామేరువులో మనకు కనిపిస్తాయి. ఇవియే విరహాంకుడి సంఖ్యలు. ఈ మేరువును మూడవ చిత్రములో చూడవచ్చు. ఈ చిత్రములో ఒకటినుండి 13 మాత్రలను ఎడమవైపు చూడవచ్చు, కుడివైపు అందులో ఉండే అక్షరముల సంఖ్య యివ్వబడ్డాయి. ఉదాహరణకు ఎనిమిది మాత్రల వృత్తములలో నాలుగునుండి (అన్నియు గురువులు) ఎనిమిది అక్షరాలు (అన్నియు లఘువులు) ఉంటాయి. ఎడమనుండి కుడివఱకు ఈ వృత్తములలోని గురువుల సంఖ్య చూపబడింది. గురువులు లేని (అన్నీ లఘువులైన) వృత్తము 1, 1 గురువుతో 7 వృత్తములు, 2 గురువులతో 15, 3 గురువులతో 10, 4 గురువులతో (లఘువులు లేవు) 1 వృత్తము ఉన్నాయి ఈ మాత్రాఛందస్సులో. వీటిని చిన్న అచ్చులోని అంకెలు తెలుపుతాయి. తొమ్మిది మాత్రల వృత్తాలలో కూడ ఐదునుండి (నాలుగు గురువులు, ఒక లఘువు) తొమ్మిది అక్షరాలు (అన్నియు లఘువులు) ఉంటాయి. దీనికి కూడ సున్న నుండి 4 గురువులు గలవు. ఈ వివరాలు చిన్న అంకెలలో చూపబడ్డాయి.

మాత్రా గణములు

ప్రాకృత పైంగలములో^{[7, 8]} ఐదు మాత్రాగణములు కనిపిస్తాయి. అవి టవర్గమునకు చెందిన ఐదు అక్షరములు. ఆఱునుండి రెండువఱకు గల మాత్రలను వరుసగా ట, ఠ, డ, ఢ, ణ గణములని అంటారు.

టట్ఠ డ ఢాణఇ మజ్ఝే
గణభేఓ హోన్తి పంచ ఆక్ఖరఓ
ఛ ప చ త దా జహసంఖం
ఛప్పం చచఉత్తి దుకలాసు – ప్రాకృతపైంగలం 1-121

ట, ఠ, డ, ఢ, ణ అనే గణభేదములు గలవు, వీటికి ఆఱు, ఐదు, నాలుగు, మూడు, రెండు కళలు (మాత్రలు) ఉండును.

టగణో తేరహ భేఓ
భేఆ అట్ఠాఇ హోన్తి ఠగణస్స
డగణస్స పంచభేఆ
తిఅ ఢగణే బే బి ణగణస్స – ప్రాకృతపైంగలం 1-131

ట గణములో 13, ఠ గణములో 8, డ గణములో 5, ఢ గణములో 3, ణ గణములో రెండు భేదములు గలవు.

ఇందులో చతుర్మాత్రాగణములకు ప్రత్యేకమైన పేర్లు కూడ ఉన్నాయి, అవి కర్ణము (గ-గ), కరతలము (స గణము), పయోధరౌ (జ గణము), ధ్రువచరణము (భ గణము), విప్ర (న-లము). జ గణమును నరేంద్ర అని కూడ అంటారు. కందములో (ఆర్యాగీతి) ఆఱవ గణమైన జగణము లేక నలమును నరేంద్ర, విప్ర అనే పేరులతో పిలువబడడం గమనార్హము.

మాత్రావృత్తములు

ప్రాకృతము, అపభ్రంశము, హిందీ భాషలలో మాత్రావృత్తములు లెక్కకు లేనన్ని ఉన్నాయి. జయదేవుడు, జానాశ్రయి కర్త, విరహాంకుడు, హేమచంద్రుడు^[9], జయకీర్తి, ప్రాకృతపైంగలకారుడు ఎన్నో మాత్రావృత్తాలను పేర్కొన్నారు. వాటి చర్చ ఈ వ్యాసపు యెల్లలను దాటుతుంది. ఉదాహరణకు ప్రసిద్ధమైన దోహాను మాత్రము వివరిస్తాను.

దోహా ఒక ద్విపద.

(1) దీనికి ప్రతి పాదములో 24 మాత్రలు ఉండాలి. దీనిని 13, 11 మాత్రలుగా విరగగొట్టాలి. కొందరు 11, 13 గా కూడ విరగగొట్టుతారు.
(2) పాదాదిలో లగము ఉండరాదు.
(3) మొదటి అర్ధములో చివర స, ర, న గణములలో ఏదైన ఉండాలి.
(4) రెండవ అర్ధపు చివరలో జ-గణమో లేక త-గణమో ఉండాలి (అంటే చివరి అక్షరము ఎప్పుడు లఘువే).
(5) అంత్యప్రాస అవసరము.
(6) తెలుగులో వ్రాస్తే ద్వితీయాక్షర ప్రాస ఉండాలి.
(7) మొదటి అక్షరానికి, రెండవ అర్ధములో మొదటి అక్షరానికి (అంటే 14వ మాత్రకు) అక్షరయతి ఉండాలి.

దోహాకు క్రింద కొన్ని ఉదాహరణలు:

అందము లన్నియు నీవెగా – నానందము నా కిమ్ము
సుందర చంద్రిక నీవెగా – సోయగముల కొక సొమ్ము

మందము మందము మారుతము – మానస మున కొక తెంపు
సందెల వెలుగుల యరుణిమలు – చక్కిలిగింతల వంపు

సాగర తీరపు సైకతము – చక్కని యూహల హాయి
రాగపు లహరుల చెలువమో – రసములు పొంగిన రేయి

చెవులకు కమ్మని విందులో – శ్రీరాగపు తానమ్ము
కవులకు నవమగు పండుగో – కామిని మధుర గళమ్ము

దేశి ఛందస్సు

సంస్కృత, ప్రాకృత, ఉత్తర భారతీయ భాషలలో వార్ణిక, మాత్రా ఛందస్సులు మాత్రమే కనబడుతాయి. కన్నడ తెలుగు భాషలలో కనిపించే దేశి ఛందస్సులో ఉపయోగించే గణములు ప్రత్యేకమైనవి. కన్నడములో వీటిని అంశ గణములని, తెలుగులో ఉపగణములని పిలుస్తారు. ఈ గణముల పుట్టుకకు బీజము రెండు మాత్రలు అని చెప్పవచ్చు. ఒక గురువుతో (U) లేక రెండు లఘువులతో (II) ప్రారంభించి మిగిలిన గణములను ఉత్పత్తి చేయవచ్చు. దీని ప్రస్తారమును గురించి నాగవర్మ ఛందోంబుధిలో^[10] ఈ విధముగా వివరిస్తాడు –

ఎరడుం మూఱుం నాల్కుం
గురువిం ప్రస్తరిస లంబునిధి గజ ధరణీ-
శ్వర గణమొగెగుమవర్కం
సరసిజభవ విష్ణు రుద్ర సంజ్ఞెగళక్కుం – నాగవర్మ ఛందోంబుధి, 5.3

రెండు, మూడు, నాలుగు గురువులతో ప్రస్తారము చేయగా నాలుగు, ఎనిమిది, 16 సంఖ్యలు ఉండే బ్రహ్మ, విష్ణు, రుద్రగణములు మనకు లభిస్తాయి.

కరపురవార్ధియాగి గురు వాదియ తద్గురువిందదఃస్థమా-
గిరె లఘుయుగ్మం క్రమదె ముంతె సమం కడెవట్ట బిణ్పినొళ్
బరె లఘువొందె పింతె లఘు ముంతె సమం మొదలిం తగుళ్దు పం-
కరుహదళేక్షణే గమనింతిడు సర్వలఘుత్వమప్పినం – నాగవర్మ ఛందోంబుధి, 5.3

ఓ పద్మాక్షీ, రెండు, మూడు, నాలుగు గురువులను ఉంచి, గురువు క్రింద రెండు లఘువులను ఉంచి, అదే విధముగా లఘుయుగ్మము క్రింద గురువును, గురువు క్రింద లఘువును ఉంచి అన్ని లఘువులు వచ్చేవఱకు వ్రాసినప్పుడు వచ్చిన గణములు యివి.

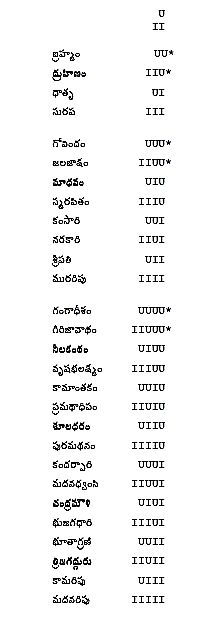
నాలుగవ పట్టిక – అంశగణములు, ఉపగణములు: కన్నడములోని బ్రహ్మ, విష్ణు, రుద్ర గణములు, వాటికి నాగవర్మ ఛందోంబుధినుండి నుండి ఉదాహరణలు ఇవ్వబడినవి. ఉదాహరణలలోని పదములన్నియు ఆ గణపు పేరును సూచించునవే. ఇందులో నక్షత్ర చిహ్నముతోటి గణములను తొలగిస్తే మనకు తెలుగులోని సూర్య, ఇంద్ర, చంద్ర గణములు లభించును.

ఈ విధముగా వ్రాసినప్పుడు జనించిన గణములను నాలుగవ పట్టికలో చూడవచ్చు. పై పద్ధతిని సులభంగా ఈ విధముగా అర్థం చేసుకోవచ్చు – ఒక గురువు, రెండు లఘువుల కుడి ప్రక్కన ఒక గురువును, ఒక లఘువును ఉంచితే మనకు నాలుగు బ్రహ్మగణములు, ఒక్కొక్క బ్రహ్మ గణపు కుడివైపున ఒక గురువును, ఒక లఘువును ఉంచితే ఎనిమిది విష్ణు గణములు, ఒక్కొక్క విష్ణుగణపు కుడివైపున ఒక గురువును, ఒక లఘువును ఉంచితే 16 రుద్రగణములు మనకు లభిస్తాయి. ఈ ఉపగణోత్పత్తి ప్రస్తారమును గురించి అప్పకవి^[11] చెప్పిన పద్ధతి నాకు నచ్చినది.

ద్వివిధం బయ్యెను గణచయ
మవని నిసర్గములు నుపగణాలియు ననఁగా
నివి నైసర్గ గణంబులు
రవిశక్రశశాంకు లివి ధరణి నుపగణముల్ – అప్పకవీయము, 4.40

గణములు రెండు విధములు – నైసర్గిక గణములు, ఉపగణములు. ఈ రవి-శక్ర-శశాంక గణములైన ఉపగణముల ప్రస్తారమును గురించి యిలా చెబుతాడు –

గరిమ నత్యుక్త మొదలుగాఁ గలుగునట్టి
మూఁట రెండేసి పంక్తులు మొదల విడిచి
మొదల లఘువున్న పంక్తులమొదల లఘువు
వెండియు నిల్ప రవిశక్రవిధు గణములు – అప్పకవీయము, 4.41

అనగా రెండవ (అత్యుక్త), మూడవ (మధ్య), నాలుగవ (ప్రతిష్ఠ) ఛందములను వ్రాయవలెను. గణము గురువుతో ప్రారంభమయినప్పుడు దానిని అలాగే ఉంచి, లఘువుతో ప్రారంభమయినప్పుడు, ముందు మరొక లఘువును ఉంచవలయును. తరువాత ఆ ఛందములలో మొదటి రెండు గణములను తొలగించగా మిగిలిన గణములు సూర్యేంద్రచంద్ర గణములు.

నాలుగవ పట్టికను మఱల జాగ్రత్తగా పరిశీలించితే ఈ విషయం అర్థమవుతుంది. కన్నడములో బ్రహ్మగణములలో నాలుగు మాత్రలైన UU, IIU గణములను తొలగిస్తే మిగిలిన UI, III తెలుగులోని సూర్యగణములు. కన్నడములోని విష్ణు గణములు – UUU, IIUU, UIU, IIIU, UUI, IIUI, UII, IIII, ఇందులో ఆఱు మాత్రలైన UUU, IIUU తొలగించగా మిగిలిన ఆఱు గణములు తెలుగులోని ఇంద్రగణములు. అదే విధముగా కన్నడములోని రుద్రగణములు – UUUU, IIUUU, UIUU, IIUU, UUIU, IIUIU, UIIU, IIIIU, UUUI, IIUUI, UIUI, IIIUI, UUII, IIUII, UIII, IIIII, ఇందులో ఎనిమిది మాత్రలైన UUUU, IIUUU తొలగించగా మిగిలినవి తెలుగులోని చంద్రగణములు. ఈ బ్రహ్మ, విష్ణు, రుద్ర గణములు జయకీర్తి ఛందోనుశాసనములో రతి, మదన, శర గణములని పేర్కొనబడ్డాయి.

ఈ అంశ లేక ఉపగణముల స్థానము ఛందశ్శాస్త్రములో విచిత్రమైనది. ఇవి పూర్తిగా మాత్రాగణములు కావు, ఎందుకంటే వీటిలోని మాత్రల సంఖ్య స్థిరము కాదు. ఉదాహరణకు, ఇంద్రగణములలో నాలుగు, ఐదు మాత్రలు ఉన్నాయి, విష్ణు గణములలో నాలుగు నుండి ఆఱు మాత్రలు ఉన్నాయి. ఈ గణములు పూర్తిగా అక్షర గణములు కాక, పూర్తిగా మాత్రా గణములు కాక, ఈ రెంటియొక్క మిశ్రిత పరిణామము అని చెప్పవచ్చు.

కన్నడ తెలుగు దేశి ఛందస్సులలో ఈ మూడు విధములైన గణములను మాత్రమే పద్యములలో వాడియున్నారు. ఇందులో ఒక గొప్ప విశేషమేమంటే ఈ గణాలలో ఎదురు నడక లేదు, అనగా లఘువు ప్రక్కన గురువు వాడకము పద్యాదిలో, పాదాదిలో లేదు. కంద పద్యపు సరిపాదములో జ-గణము ఉండవచ్చును. కాని యిది వేరు విషయము. కందపు రెండు పాదములను ఒకే పాదముగా గ్రహించడము కూడ అమలులో ఉన్నది. ఎదురు నడక లేని పద్యములు, పాదములు యీ రెండు భాషల దేశి ఛందస్సులోని ఒక విచిత్రమైన ప్రత్యేకత. తెలుగులో చంద్రగణములున్న పద్యములు అక్కఱలు, షట్పది. కాని వీటిలో చంద్రగణములేని మధ్యాక్కఱను మాత్రమే తెలుగు కవులు ఉపయోగించారు. తెలుగు కవులు (ఒకరిద్దరు మినహా) దేశి ఛందస్సులో సూర్యేంద్రగణములున్న పద్యములను మాత్రమే వాడారు.

తెలుగులో చివరి గురువుతో సూర్యగణములు లేకున్నా, నన్నయభట్టు ఆంధ్రమహాభారతములో గ-గమును, స-గణమును సూర్యగణములుగా అక్కడక్కడ వాడాడు ^[12]. సీసము, తేటగీతి వంటి పద్యాలను పాడేటప్పుడు చివర నుండే సూర్యగణపు లఘువును పాడేటప్పుడు పొడిగించి పాడుతారు. అక్కడ ఒక విరామము కూడ ఉంటుంది. అందువలన ఒక విధముగా చూస్తే చివర ఉండే గ-లము గ-గమే, న-గణము స-గణమే. సూర్యేంద్రగణములకు బదులు బ్రహ్మ విష్ణు గణములను వాడి కొన్ని పద్యాలను నేను వ్రాసియున్నాను, మచ్చుకు కొన్ని ఉదాహరణలు –

మధ్యాక్కఱ – (వి-వి-బ్ర) (వి-వి-బ్ర)

కవనాల వ్రాసేను నీకై – కావ్యమ్ము లల్లేను నీకై
భవనాల గట్టేను నీకై – పలు దివ్వె లుంచేను నీకై
నవగీతి బాడేను నీకై – నాట్యమ్ము జేసేను నీకై
భువనాల దొర మోహనాంగా – ముద మీయ రా వేగ రంగా

ద్విపద – (వి-వి) (వి-బ్ర)

ఆనంద మ్మయెగదా – యందమ్ము గనగా
ఆనంద మ్మయెగదా – యా నందు గనగా
ఎందుకే తహతహ – యెందుకే హృదిలో
ఎందుకే చెప్పవే – యెవ్వరే మదిలో

ఆటవెలది – (బ్ర-బ్ర-బ్ర) (వి-వి) / (బ్ర-బ్ర-బ్ర) (బ్ర-బ్ర)

మనసా యెందు కిట్లు – మమతల వలలందు
బంధించుచు నుంటివిగా – వదలకుండ
మనసా యెందు కిట్లు – మౌనపు నాదమ్ము
మ్రోగించుచు నుంటివిగా – రాగమయమై

మనసా యెందు కిట్లు – మాయల యుయ్యాల
నూగించుచు నుంటివిగా – నూహ లేక
మనసా యెందు కిట్లు – మత్తుల మదిరలన్
ద్రాగించుచు నుంటివిగా – దప్పి దీర్చ

తేటగీతి – (బ్ర-వి-వి) (బ్ర-బ్ర)

అవి మేఘములా నీ యా కురు – లవి మేఘములా
అవి రాగములా నీ యా నుడు – లవి రాగములా
అవి తామరలా నీ యా కను -లవి తామరలా
అవి శాపములా నీ కనుచూపు – లవి శాపములా

అంశగణ ప్రస్తారము – మేరువు

ఇలా గణప్రస్తారము ఈ మూడు విధములైన గణములకు మాత్రమే పరిమితము చేయడము ఒక సౌలభ్యము మాత్రమే. నిజముగా ఈ విధంగా ఎన్నో ఛందస్సులను సృష్టి చేయడానికి వీలవుతుంది. అలా చేస్తే ఈ అంశ గణముల ఛందస్సును మనకు వార్ణిక ఛందస్సు, మాత్రాఛందస్సుల వలె పెంచవచ్చు. దీనికి కూడ ఒక మేరువును కల్పించవచ్చు. వీటిలో కూడ క్రొత్త వృత్తములను పుట్టించవచ్చు. వీటిని కూడ వృత్త సంఖ్యలతో గుర్తించవచ్చు.

ఒక ఛందములో వృత్త సంఖ్య కావలసినప్పుడు, ముందు అది ఎన్నవ ఛందమో తెలిసికోవాలి. ఉదాహరణకు అది 12వ ఛందమనుకొందాము. దాని గురులఘువులు UIU UIU UIU UIU అయితే, అది 12వ ఛందములోని 1756వ వృత్తము. కాని అదే ఛందములోని వృత్తము IIII UII IIII UU అయితే ఇందులో మొదటి లఘువు తొలగిస్తే మనకు 12 అక్షరాల III UII IIII UU వృత్తము లభిస్తుంది. దీని వృత్త సంఖ్య 1016. IIII UII IIII UU వృత్తము 13 అక్షరముల అతిజగతి ఛందములోని 2031వ వృత్తమైన మదకలిత. అప్పకవి వివరణ యిలా వృత్త సంఖ్యను తేలికగా మనకు తెలుపుతుంది.

మనకు ఒక ఛందములోని వృత్త సంఖ్య యివ్వబడితే, అందలి గురులఘువులను వార్ణికఛందస్సులో తెలిపిన విధముగా మనము కనుగొనవచ్చు. ఆ అమరిక గురువుతో ప్రారంభమయితే అలాగే ఉంచాలి, లఘువుతో ప్రారంభమయితే, దానికి ముందుగా మరొక లఘువును జత చేయాలి. ఈ విధముగా మనము వృత్త సంఖ్యనుండి గురు-లఘువుల అమరికను కనుగొనవచ్చు.

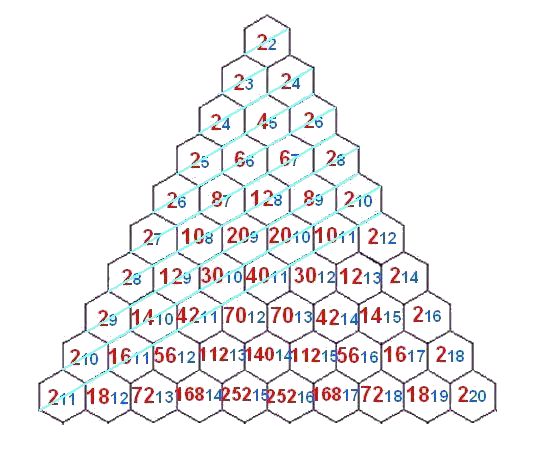
చిత్రము 4. అంశగణమేరువు. వృత్తముల సంఖ్య పెద్ద అచ్చులో, మాత్రల సంఖ్య చిన్న అచ్చులో చూపబడ్డాయి. ఉదాహరణకు నాలుగవ ఛందములో 5 మాత్రల వృత్తములు (UIII, IIIII) 2, 6 మాత్రల వృత్తములు (UIIU, IIIIU, UIUI, IIIUI, UUII, IIUII) 6, 7 మాత్రల వృత్తములు (UIUU, IIIUU, UUIU, IIUIU, UUUI, IIUUI) 6, 8 మాత్రల వృత్తములు (UUUU, IIUUU) 2 ఉన్నాయి. ఇవి కన్నడములోని రుద్ర గణములు. ఇందులో కుడివైపు 8 ఎనిమిది మాత్రల 2 వృత్తములను తొలగిస్తే మనకు తెలుగులోని చంద్ర గణములు లభిస్తాయి.

అంశగణములకు ఒక మేరువును కూడ సృష్టించవచ్చు. ఇలా సృష్టించిన మొట్టమొదటి మేరువును నాలుగవ చిత్రములో చూడవచ్చు. ఇందులోని త్రిభుజపు క్రింది భుజము పదవ ఛందమునకు వర్తిస్తుంది. ఇందులోని వృత్తముల మొత్త సంఖ్య – 2¹⁰, అనగా 1024. ఈ పదవ ఛందములోని గణములలోని అక్షరముల సంఖ్య 10, 11. ఎందుకంటే ప్రస్తారారంభములో పది గురువులతో మొదలు పెట్టి చివర 11 లఘువులతో ముగిస్తాము. ఈ ఛందములోని వృత్తములలో మాత్రల సంఖ్య 11 నుండి 20. 11 మాత్రల వృత్త సంఖ్య 2; 12 మాత్రల వృత్త సంఖ్య 18; 13 మాత్రల వృత్త సంఖ్య 72; 14 మాత్రల వృత్త సంఖ్య 168; 15 మాత్రల వృత్త సంఖ్య 252; 16 మాత్రల వృత్త సంఖ్య 252; 17 మాత్రల వృత్త సంఖ్య 168; 18 మాత్రల వృత్త సంఖ్య 72; 19 మాత్రల వృత్త సంఖ్య 18; 20 మాత్రల వృత్త సంఖ్య 2. వృత్త సంఖ్య ఎఱ్ఱ రంగులో, మాత్రల సంఖ్య నీలి రంగులో చూడవచ్చు. మొదటి చిత్రపు మేరువులోని సంఖ్యలను రెట్టింపు చేస్తే మనకు ఈ చిత్రములోని మేరువు లభిస్తుంది. అదే వీటి రెంటికి ఉన్న భేదము.

రెండవ, మూడవ, నాలుగవ ఛందములకు సరిపోయే అడ్డముగా ఉండే వరుసలలోని సంఖ్యలు కన్నడములోని బ్రహ్మ, విష్ణు, రుద్ర గణాలకు సరిపోతాయి. ఈ వరుసలలో చివరి అంకెలను వదలి వేసినప్పుడు మనకు తెలుగులోని సూర్య, ఇంద్ర, చంద్ర గణముల సంఖ్యలు దొరకుతాయి.

ఇందులోని నీలపు రంగు గీతలు ఒకే మాత్రలున్న వేరువేరు ఛందములలోని పద్యముల సంఖ్యలను కలుపుతాయి. ఈ సంఖ్యల మొత్తము కూడ ఒక విరహాంకశ్రేణిని పుట్టిస్తుంది. ఆ సంఖ్యలు – 2, 2, 4, 6, 10, 16, 26, 42, … ఇవి 1, 1, 2, 3, 5, 8, 13, 21, …సంఖ్యల రెట్టింపు. ఎదురునడక లేని మాత్రాగణములు కూడ ఫిబనాచ్చి సంఖ్యలను అనుసరిస్తాయని నేను మొదటే తెలిపియున్నాను.

కన్నడములో ఇటీవలి శతాబ్దములలో అంశగణములకు బదులు మాత్రాగణములనే ఎక్కువగా వాడారు, ఉదాహరణకు సీస పద్యమంటే పంచమాత్రాబద్ధమైన సీసమే. ప్రస్తుతము తెలుగులో మాత్రమే ఉపగణములను ఉపయోగిస్తున్నారని అంటే అతిశయోక్తి కాదు. ఉపగణాలతో నుండే జాత్యుపజాతులలో ఎంతయో వైవిధ్యము ఉంది. ఒక ద్విపద పాదమును 432 విధములుగా, ఒక కందపు ఎనిమిది గణముల పాదమును 12800 విధములుగా, ఒక మధ్యాక్కఱ పాదమును 5184 విధములుగా, ఒక ఉత్సాహ పాదమును 128 విధములుగా, ఒక తరువోజ పాదమును, ఒక సీస పద్యపు పాదమును 186624 విధములుగా, ఒక వృషభగతి రగడ పాదమును 4096 విధములుగా, ఒక ఆటవెలది రెండు పాదములను 9216 విధములుగా, ఒక తేటగీతి పాదమును 288 విధములుగా వ్రాయవచ్చు.

క్రొత్త బీజములు – క్రొత్త గణములు

అంశ లేక ఉపగణముల సృష్టి విధానమును సార్వత్రికము చేయవచ్చు. రెండు మాత్రల ఒక గురువు లేక రెండు లఘువులను గణోత్పత్తికి బీజముగా నెంచుకొనడానికి బదులు, మూడు మాత్రలైన UI, IU, III ను బీజముగా తీసికొని వీటికి పదేపదే కుడివైపు గురులఘువులను ఉంచితే లభించిన గణములకు నేను వాణీ-శ్రీ-గిరిజా గణములని పేరుంచాను.

మూడు వాణీగణములు – III, UI, IU,
ఆఱు శ్రీగణములు – IIII, IIIU, UII, UIU, IUI, IUU,
12 గిరిజా గణములు – IIIII, IIIIU, IIIUI, IIIUU, UIII, UIIU, UIUI, UIUU, IUII, IUIU, IUUI, IUUU.

సూర్యేంద్రచంద్రగణములకు బదులు వాణీశ్రీగిరిజా గణములను ఉపయోగించి పద్యములను వ్రాయవచ్చు. సూర్యేంద్ర గణములకు బదులు వాణీ-శ్రీ గణములతో ఒక తేటగీతి లాటి పద్యమును క్రింద చదువవచ్చు –

“తేటగీతి” (వాణీ-శ్రీ గణములతో)-

మనసు వరించె తరించ – ననఘ నిన్ను
కనుల కనికరించు మించు – కైన యిపుడు
హరీ బిరాన జేరర – పరాకు విడి
విరుల సరాల వేతును – శిరమునందు

మూడు మాత్రలకు బదులు నాలుగుమాత్రల బీజముతో ప్రారంభిస్తే మనకు లభించే గణములు క్రింది విధముగా ఉంటాయి –

5 పృథ్వీ గణములు – IIII, IIU, UII, IUI, UU
10 ఆకాశ గణములు – IIIII, IIIIU, IIUI, IIUU, UIII, UIIU, IUII, IUIU, UUI, UUU
15 తేజో గణములు – IIIIII, IIIIUI, IIUII, IIUUI, UIIII, UIIUI, IUIII, IUIUI, UUII, UUUI, IIIIIU, IIIIUU, IIUIU, IIUUU, UIIIU, UIIUU, IUIIU, IUIUU, UUIU, UUUU

ఎదురునడకల గణములు

కన్నడములో, తెలుగులో ఎదురు నడకతో నుండే పద్యాలు దేశి ఛందస్సులో లేవు. దీనికి కారణము ఈ గణముల సృష్టి విధానము, వీటికి బీజమైన రెండు మాత్రల ఒక గురువు, రెండు లఘువులు. కాని సంస్కృతములో, మిగిలిన ఉత్తర భాషలలో, తమిళ మలయాళ భాషలలో ఎదురు నడక ఉన్నది. వరుసగా ఎనిమిది ల-గములతో నుండే పంచచామర వృత్తము ఎదురునడకతో ప్రారంభమవుతుంది గదా! ఒక లఘువును బీజాక్షరముగా తీసికొని ఇంతకు ముందు చెప్పిన రీతులలో కుడివైపు గురు లఘువులను ఉంచి, మనము క్రొత్త గణములను సృష్టించవచ్చును. ఈ గణముల మేరువు అక్షర గణముల మేరువు వంటిదే. వీటితో నిర్మింపబడిన వృత్తములలో సగము ఎదురు నడక గలవే! ఇట్లు పుట్టించిన గణములు –

మొదటి ఛందము – ఒక గణము – I
రెండవ ఛందము – రెండు గణములు – IU, II
మూడవ ఛందము – నాలుగు గణములు – IUU, IUI, IIU, III
నాలుగవ ఛందము – ఎనిమిది గణములు – IUUU, IUUI, IUIU, IUII, IIUU, IIUI, IIUU, IIUI, IIIU, IIII

సూర్య గణములకు బదులు IU, II, ఇంద్రగణములకు బదులు IUU, IUI, IIU, III ఉపయోగించి వ్రాసిన రెండు పద్యములను క్రింద చదువవచ్చును.

ఆటవెలది “వంటి” పద్యము –

చెలువపు సిరి – కలయై నిలిచె
వలపుల విరి – పలుకదో
మిలమిల యని – మెఱిసె మదిలో
వలపుల నది – వఱదలై

తేటగీతి “వంటి” పద్యము –

హరీ యనంగా మనసు – చరించెను
హరిన్ గనంగా గనులు – తరించెను
హరీ బిరాన గనరా – వరించరా
హరీ హరీ హరిహరీ – హరిహరీ

కవితా సామగ్రి పేటికలో క్రొత్త పనిముట్లు

తెలుగులో నవీన యుగములో ఎదురు నడకతో ఎన్నో కవనాలు ఉన్నాయి. శ్రీశ్రీ గేయాలు ఇట్టి కవితలలో ఒక విశిష్ఠ స్థానాన్ని సంపాదించుకొన్నాయి. మనము తరచుగా ఉపయోగించినా, అరుదుగా నుపయోగించినా మన కవితా సామాగ్రి పేటికలో అన్ని విధములైన పనిముట్లు ఉండాలని నా భావన. అందువలన నాలుగు బ్రహ్మ గణములతోబాటు, ల-గమును (IU) కూడ చేర్చి, వీటికి చైత్ర గణములని పేరుంచాను. ఈ ఐదు చైత్ర గణములకు పదేపదే గురులఘువులను ఉంచితే పది శ్రావణ గణములు లభిస్తాయి. ఈ పది శ్రావణ గణములకు ప్రక్కన గురులఘువులను ఉంచితే 20 మార్గశీర్ష గణములు పుట్టుతాయి.

చైత్ర గణములు – IU, UI, UU, IIU, III
శ్రావణ గణములు – IUU, UIU, UUU, IIUU, IIIU, IUI, UII, UUI, IIUI, IIII
మార్గశీర్ష గణములు – IUUU, UIUU, UUUU, IIUUU, IIIUU, IUIU, UIIU, UUIU, IIUIU, IIIIU, IUUI, UIUI, UUUI, IIUUI, IIIUI, IUII, UIII, UUII, IIUII, IIIII

ఈ చైత్రగణముల సమూహములో బ్రహ్మగణములు ఒక చిన్న ఉపసమూహము, ఆ బ్రహ్మగణ ఉపసమూహములో సూర్యగణములు మరొక ఉపసమూహము. అలాగే శ్రావణ, మార్గశీర్ష గణములు కూడ. ఈ నిర్మాణమును క్రింది విధముగా తెలుపవచ్చు –

చైత్ర గణములు -> బ్రహ్మ గణములు -> సూర్య గణములు
శ్రావణ గణములు -> విష్ణు గణములు -> ఇంద్ర గణములు
మార్గశీర్ష గణములు -> రుద్ర గణములు -> చంద్ర గణములు

క్రింద ఈ గణాలతో ద్విపద, తేటగీతి లాటి పద్యాలను చదువవచ్చు –

“ద్విపద” –

వసంత కాలము – వచ్చెను గాదా
రసార్ణవ మ్మిక – బ్రదు కగు గాదా
అసీమ మగు జగ – మందపు ప్రతియై
వసించు మనసున – ప్రమోద శ్రుతియై

“తేటగీతి” –

మనసా యెందు కీ యాటలు – మఱల మఱల
మనసా యెందు కీ పాటలు – మఱల మఱల
కనులు వెదకిన నిలుచునే – గనుల ముందు
మనసా రాడె వాడు వాని – మఱచిపోవే

వివిధ ఛందోరీతుల ఏకీకరణ

భారతీయ భాషలు సంస్కృత, ప్రాకృత ఛందస్సు సిద్ధాంతములను ఆధారము చేసుకొని వర్ధిల్లాయి. ముఖ్యముగా ద్రావిడ భాషలలో, దేశి ఛందస్సు కూడ వర్ధిల్లింది. కాని తమిళ భాష ఛందస్సు వీటికి భిన్నముగా తనదయిన ఒక మార్గమును^[13] ఎన్నుకొని కొనసాగింది. ఇందులో కూడ కొన్ని ఛందములకు సంస్కృతముతో సామ్యము ఉన్నది (ఉదా. మత్తకోకిల). తమిళ ఛందస్సుపైన ఆధారపడిన పద్యాలు పాడుటకై అల్లినవి. ఈ తమిళ ఛందస్సులోని గణములను (శీరులను) మనకు పరిచితమయిన గురు-లఘువుల రూపములో వ్రాయుటకు మొట్టమొదట టేకుమళ్ళ రాజగోపాలరావు^[14] ప్రయత్నించాడు. నేను ఈ మధ్య దానిని కొనసాగించాను. ఈ నా ప్రయత్నమును ఐదవ పట్టికలో గమనించవచ్చు. బ్రహ్మ (సూర్య), విష్ణు (ఇంద్ర), రుద్ర (చంద్ర) గణములను మాత్రము తీసుకొంటే తమిళ ఛందస్సులోని కొన్ని గణములకు సమమయిన గణములు మనకు దొరకవు. కాని నేను ప్రతిపాదించిన చైత్ర, శ్రావణ, మార్గశీర్ష గణములకు తమిళ శీరులకు సామ్యము ఎక్కువగా ఉన్నది. అనగా, మన సోదర భాషయైన తమిళ పద్యాలను బోలిన పద్యములను మనము తెలుగులో కూడ వ్రాయవచ్చును. ఇట్టి గణములను ఎన్నుకొనవలసిన ఆవశ్యకతకు ఇది మరొక ముఖ్యమైన కారణము అని నేను భావిస్తాను.

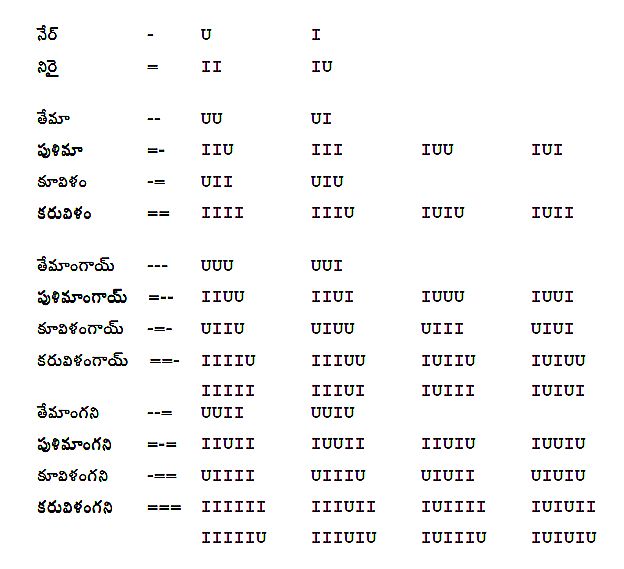
ఐదవ పట్టిక – తమిళ శీరులు: తమిళ ఛందస్సులో ఉపయోగించబడే కొన్ని గణములు, వాటి గురులఘువుల అమరిక ఇక్కడ చూడవచ్చు. ఇందులో నేర్ అనే అశై – చిహ్నముతో, నిరై అనే అశై = చిహ్నంతో చూపబడినవి.

ముగింపు

నిరంతరమైన తపస్సులో ఏకాంతవేళలో ఎదలో జనించిన భావవీచికలకు ఒక రూపాన్ని ఇవ్వడానికి తగిన పద్య ఫలకమును ఎన్నుకొని పదాలను ఏర్చి పద్యమును కూర్చుటకు కవి ప్రయత్నము చేస్తాడు. ఒకే భావాన్ని ఎన్నో విధములైన పదాలతో ఎన్నో విధములైన పద్యాలలో ఇముడ్చగలుగుతుంది రసాంతరంగిణియైన కవయిత్రి. కాని ఈ పద్యములు విచిత్రమైన గణిత శాస్త్రపు బీజోత్పన్నములు. అది అక్షర గణాలపై ఆధారపడిన ఛందస్సు కావచ్చు, మాత్రాగణాలపైన ఆధారపడిన ఛందస్సు కావచ్చు, ఉభయ గుణగణ స్రవంతులను సంగమించుకొన్న అంశగణాధారమైన ఛందస్సు కావచ్చు, ఇవేవి కాక ఈ సిద్ధాంతాలను ప్రాతిపదిక చేసుకొన్న క్రొత్త ఛందస్సు కావచ్చు. ఛందస్సు ఒక మహాసాగరము. ఆ సాగరపు టలలు మానవుని కలలకు ఆకారశిల్పము నిచ్చి కలకాలము నిలిచేటట్లు చేయగలవు. అదియే ఆదికాలమునుండి నేటివఱకు వివిధ దేశాలలో కారణజన్మభూతుడైన కవిఋషి చేసే కళామయ కృషి.

గ్రంథసూచి

1. ఛందోదర్పణము – అనంతామాత్యుడు – సం. చిర్రావూరి శ్రీరామశర్మ, రోహిణీ పబ్లికేషన్స్, రాజమండ్రి, 1998.
2. అనంతుని ఛందము – అనంతామాత్యుడు – సం. గిడుగు సీతాపతి, వావిళ్ళ రామస్వామి శాస్త్రులు అండ్ అస్న్స్, మదరాసు, 1921.
3. Chandah sutra of pingalacharya with the commentary by halayudha – ed. pandita visvanAtha Sastri, ganesa Press, Calcutta, 1874.
4. వృత్తజాతి సముచ్చయ – విరహాంక – సం. హరి దామోదర్ వేళంకర్, రాజస్థాన ప్రాచ్యవిద్యా ప్రతిష్ఠాన, జోధ్పుర్, 1962.
5. The so-called Fibonacci numbers in ancient and medieval India – Paramanand Singh – Historia Mathematica, 12, 229-244, 1985.
6. The Art of Computer Programming – Volume 4 – History of Combinatorial Generation – Donald E. Knuth, Addison Wesley Press, Boston, 2006.
7. ప్రాకృతపింగలసూత్రాణి – సం. శివదత్త, కాశీనాథ పాండురంగ్ పరబ్, నిర్ణయసాగర్ ప్రెస్, 1894.
8. మాత్రికా ఛందోం కా వికాస్ – శివనందన ప్రసాద్, బిహార్ రాష్ట్రభాషా పరిషద్, పట్నా, 2000.
9. ఛందోనుశాసన – హేమచంద్ర సూరి – సం. హరిదామోదర్ వేళంకర్, భారతీయ విద్యా భవన్, బొంబాయి, 1961.
10. ఛందోంబుధి – ప్రథమ నాగవర్మ – సం. H S రామస్వామి అయ్యంగార్, శ్రీవత్సా ప్రెస్, మదరాసు, 1946.
11. అప్పకవీయము – కాకునూరి అప్పకవి – సం. గిడుగు రామమూర్తి పంతులు, ఉత్పల నరసింహాచార్యులు, వావిళ్ళ రామస్వామి శాస్త్రులు అండ్ సన్స్, మదరాసు, 1934.
12. తెలుగు భాషలో ఛందోరీతులు – రావూరి దొరసామిశర్మ, వెల్డన్ ప్రెస్, మదరాసు, 1962.
13. A reference grammar of Classical Tamil poetry – V S Rajam, American Philosophical Society, Philadelphia, 1992.
14. A Comparative prosody of Dravidian languages – T Rajagopal Rao, South Indian Literary Research Institute, 1913.
15. జానాశ్రయి – జనాశ్రయ మాధవ వర్మ, గుణస్వామి – సం. మానవల్లి రామకృష్ణకవి, తిరుమల తిరుపతి దేవస్థానం ప్రెస్, తిరుపతి, 1950.
16. రత్నమంజూష – సం. హరి దామోదర్ వేళంకర్, భారతీయ జ్ఞానపీఠ, కాశి, 1944.