జార్జ్ బూల్

శ్రీశ్రీ “చరమరాత్రి” అనే కథొకటి రాశాడు. అది ఆత్మహత్య చేసుకోబోతూ కథానాయకుడు చేసే తాత్విక ఘోష. జీవితమొక కఠోరమైన, గందరగోళమైన బీజగణిత సమస్య, అది ఏ తర్కానికీ లొంగదంటూ 1 + 1 = 1 అని ఉగ్గడిస్తాడు. అంటే శూన్యం కన్నా, అనేకం కన్నా ఏకం గొప్పదట.

కానీ, పందొమ్మిదో శతాబ్దపు మధ్యలో జార్జ్ బూల్ (George Boole) అనే గొప్ప బ్రిటిష్ మేధావి ఓ కొత్త బీజ గణితాన్ని తయారు చేసాడు. అది కచ్చితమైన సూత్రాల ప్రకారం పనిచేస్తుంది. దాని ప్రకారం ఒకటికి ఒకటి కలిపితే వచ్చేది ఒకటే. (1 + 1 = 1) కొత్త గణితం పేరిట ఇప్పటి బడి పిల్లలు దానిని నేర్చుకుంటారు. శాఖోపశాఖలుగా విస్తరించిన గణితశాస్త్రంలో అనేక కొత్త విభాగాలకి బూల్ బీజగణితమే ఆధారం. అంతకన్నా ఆశ్చర్యమైనదీ, అప్పట్లో ఎవరూ ఊహించనిదీ, మనం ఇప్పుడు వాడే కంప్యూటర్లకి ఆధారం బూల్ బీజగణితమే! కంప్యూటర్ ప్రోగ్రామర్లలో బూల్ పేరు తెలియని వాళ్ళైనా, “బూలియన్” అన్నపదాన్ని రోజూ వాడకుండా ఉండరు. అలా బూల్ చిరస్థాయిగా ఉండిపోయాడు.

వాస్తవానికి, ఇంటర్నెట్ వాడే వాళ్ళంతా తమకు తెలియకుండానే బూల్ గణితాన్ని వాడుతున్నారు! ఉదాహరణకి, కొడవటిగంటి కుటుంబరావు రచనల కోసం వెతకాలనుకున్నారనుకోండి. ఇంటర్నెట్లో “కుటుంబరావు” అన్న పదం ఇచ్చి వెతకమంటే, కుటుంబరావు అన్న పదం ఉన్న రచనలన్నీ వస్తాయి – వాటిల్లో కొన్ని (మనం కోరుకోకపోయినా) కుటుంబరావు అని పేరున్న పాత్రకి సంబంధించినవీ, “అక్కినేని కుటుంబరావు” అన్న రచయిత రాసినవీ ఉండొచ్చు. “కొడవటిగంటి” అన్న పదం ఇస్తే, “కొడవటిగంటి” అన్న పదం ఉన్న రచనలన్నీ వస్తాయి. వాటిల్లో మనం కోరుకోకపోయినా “కొడవటిగంటి” అన్న పదమూ “రోహిణీప్రసాద్” అన్న పదమూ ఉన్న రచనలూ ఉంటాయి. “కొడవటిగంటి” “కుటుంబరావు” అని రెండు పదాలనీ ఇస్తే, ఆ రెండూ ఉన్న రచనలే వస్తాయి. ఏదో ఒక్కటే ఉన్న రచనలు రావు. కాని వీటిలో కొడవటిగంటి రోహిణీప్రసాద్, అక్కినేని కుటుంబరావు అన్న ఇద్దరి పేర్లూ ఉన్న రచనలూ వస్తాయి. “కొడవటిగంటి కుటుంబరావు” అని వెతికితే మాత్రం కొడవటిగంటి, దాని వెంటనే కుటుంబరావు అన్న పదాలున్న రచనలే వస్తాయి.. ఈ శోధన తర్కం ఆధారపడి ఉన్నది బూల్ గణితం మీదనే!

బూల్ జీవిత సంగ్రహం

బూల్ బీజగణితం గురించి తెలుసుకునే ముందర స్పూర్తిదాయకమైన అతని జీవితం గురించి తెలుసుకుందాం. మనమింతకు ముందు చదివిన లైబ్నిజ్, బాబేజ్‌లు ఉన్నత కుటుంబాల నుండి వచ్చినవాళ్ళు. ఒకరి తండ్రి ప్రొఫెసరయితే, మరొకరి తండ్రి బ్యాంకర్. కానీ, బూల్ చాలా క్రింద తరగతి నుండి వచ్చినవాడు. అతని తండ్రి చెప్పులమ్మి బతికాడు. తల్లి పనిమనిషి. బూల్ కి యూనివర్సిటీ కెళ్ళే భాగ్యం కూడా కలగలేదు. ఈ పరిస్థితుల్లో పెరిగిన అతను గొప్ప వ్యక్తిత్వం సంపాదించాడు.

జార్జ్ బూల్ తండ్రి జాన్ బూల్ ఇంగ్లాండు లోని లింకన్ అనే ఊళ్ళో చెప్పులు తయారు చేసేవాడు. జాన్ బూల్ ఇరవైమూడో ఏట లండన్ వెళ్ళాడు. అక్కడా చెప్పులు చేసే పనిలోకే దిగి దుర్భరమైన పరిస్థితులు ఎదుర్కొన్నాడు. వృత్తి మీద కలిగిన జుగుప్స నుండి స్వాంతన పొందడానికి గణిత విజ్ఞానశాస్త్రాల మీద మక్కువ పెంచుకుని పుస్తకాలు చదివేవాడు. కులీనుల ఇళ్ళలో పనిచేసే “మేరీ” అన్న ఆమెని పెళ్ళి చేసుకున్నాడు. పెళ్ళయిన తర్వాత వాళ్ళిద్దరికీ లండన్‌లో కలిసి ఉండే తాహతు లేక లింకన్‌కి తిరిగి వచ్చి ఓ చిన్న చెప్పుల షాపు తెరిచారు. వాళ్ళకి పెళ్ళయిన పదేళ్ళకి, 1815లో, జార్జ్ బూల్ పుట్టాడు. తరవాత మరో ముగ్గురు పిల్లలు పుట్టారు. జార్జ్ చిన్నప్పటినించీ పుస్తకాలంటే ఇష్టపడేవాడు. బళ్ళో మిగిలిన పిల్లల కంటే చదువులో చాలా ముందుండేవాడు. తండ్రి నుండి విజ్ఞానకాంక్ష, తల్లి నుండి మృదుస్వభావం వారసత్వంగా సంపాదించాడు. పేద కుటుంబంలో పుట్టినా జార్జ్ బూల్ సంతోషమైన కుటుంబ వాతావరణంలో పెరిగాడు. సైన్సు మీదే కాక సాహిత్యం అంటే కూడా అభిలాష చూపించేవాడు, లాటిన్, గ్రీకు భాషల్లో కవిత్వం చదివేవాడు. పధ్నాలుగేళ్ళ వయసులో లింకన్ పట్టణంలో జరిగిన ఓ చిన్న వివాదం అతని వ్యక్తిత్వానికి నిదర్శనంగా నిలుస్తుంది. జార్జ్ ఓ గ్రీకు కవితని అనువదించి స్థానిక పత్రికలో ప్రచురించాడు. సంపాదకులు ఆశ్చర్యపోయారు – పధ్నాలుగేళ్ళ పిల్లవాడు చేసిన అనువాదమంటే నమ్మలేకపొయ్యారు. ఓ పాఠకుడు జార్జ్ గ్రంథచౌర్యం చేశాడని ఆరోపించాడు. జార్జ్ చూస్తూ ఊరుకోలేదు. ఎదురు తిరిగాడు; అనువాదం తన సొంతమేననీ, తన మీద అనుమానం ఉంటే ఎక్కడ నుంచి గ్రంథచౌర్యం చేశానో చెప్పమని ఆ పాఠకుడిని ధైర్యంగా, పత్రికాముఖంగా నిలదీశాడు. ఈ పత్రికావివాదం మూలంగా లింకన్ పట్టణ ప్రజలకి ఒకటి మాత్రం తెలిసిపోయింది – తమ మధ్య ఓ బాల మేధావి ఉన్నాడని! గొడవల్లో తల దూర్చడం జార్జ్ కి ఇష్టం ఇష్టం లేకపోయినా, తన ఆదర్శాలని ధైర్యంగా కాపాడుకొనేవాడు.

జార్జ్ కుటుంబానికి అతనిని బడికి పంపే స్తోమతు లేదు. జార్జ్ చర్చిలో పూజారి (priest) అవుదామనుకున్నాడు. కానీ, అప్పటికే అతనికి మతం గురించి కొన్ని నిశ్చితాభిప్రాయాలేర్పడ్డాయి. చర్చి ఉపదేశాల్లో అతనికి నమ్మకం లేదు. ఏసుప్రభువుకి దైవత్వాన్ని ఆపాదించలేకపోయాడు. విశ్వంలోని ఏకత్వాన్ని దైవంతో సమానంగా చూశాడు. (ఈ నమ్మకమే తరువాత విశ్వానికి “1” ని సంకేతంగా ఇవ్వడానికి కారణమయి ఉండవచ్చు.) ఈ నమ్మకాల మూలంగా ఇంగ్లాండు చర్చి సభ్యత్వ దరఖాస్తులో మనస్సాక్షిగా సంతకం చెయ్యలేకపోయాడు. దానితో పూజారి అయే ఆలోచనకి స్వస్తి చెప్పాడు.

జార్జ్ తండ్రి తరచుగా ఊపిరితిత్తుల వ్యాధితో బాధపడేవాడు. తండ్రి ఆరోగ్యం క్షీణించడంతో వ్యాపారం దెబ్బతింది. దానితో తల్లిదండ్రులనీ, తమ్ముళ్ళనీ, చెల్లెలినీ పోషించాల్సిన బాధ్యత పదహారేళ్ళ జార్జ్ భుజాల మీద పడింది. కుటుంబ పోషణ కోసం లింకన్‌కి నలభై మైళ్ళ దూరంలో ఉన్న ఒక బడిలో సహోపాధ్యాయుడిగా చేరాడు. కానీ జార్జ్ అక్కడ రెండేళ్ళకన్నా ఎక్కువ ఉండలేకపోయాడు. తీరిక వేళల్లో గణితశాస్త్రం స్వయంగా నేర్చుకునేవాడు. చర్చిలో కూడా గణిత సమస్యలని సాధించేవాడు. మతప్రభావితులైన విద్యార్థుల తల్లిదండ్రులు దీనిని సహించలేకపోయారు. వాళ్ళతో ఏకీభవించిన బడి యాజమాన్యం రెండేళ్ళలోనే బూల్‌ని పనిలోనుంచి తీసేసింది. ఈ రెండేళ్ళలో (1831-1833) జరిగిన రెండు విషయాలు ఇక్కడ ప్రస్తావించాలి: గణితశాస్త్ర పుస్తకాలున్న గ్రంథాలయమేదీ బూల్‌కి అప్పట్లో దగ్గరగా లేనందువల్ల బూల్ తన చాలీచాలని జీతంతోనే పుస్తకాలు కొనుక్కునేవాడు. గణితశాస్త్ర పుస్తకాలే మిగతా వాటికన్నా చవక, పైగా, అవి ఎక్కువకాలం చదువుకోగలిగేవాడు. అలా తన లేమితనమే గణితంమీద ఆసక్తి పెరగడానికి కారణమని బూల్ పెద్దయిన తర్వాత చెప్పుకున్నాడు. 1833లో ఓ సాయంత్రం బడి దగ్గర పొలం దాటుతుంటే బూల్‌కి మెరుపులా ఓ ఆలోచన వచ్చింది – తర్కానికీ బీజగణితానికీ లంకె పెట్టొచ్చని! ఈ ఆలోచన అతనిని జీవితాంతమూ అంటిపెట్టుకునే ఉంది. మరో పదిహేనేళ్ళకి వేరే వివాదం సందర్భంగా కలిగిన స్ఫూర్తితో ఈ ఆలోచన సఫలమయింది. దాని గురించి తర్వాత తెలుసుకుందాం.

బూల్ తరవాత వేరే బడిలో చేరాడు కాని అక్కడ పరిస్థితులు నచ్చక వదులుకున్నాడు. తల్లిదండ్రుల వయసు పెరిగే కొద్దీ బూల్ కుటుంబ భారం ఎక్కువ కాసాగింది. వేరే వాళ్ళ పంచన పనిచేస్తే లాభం లేదని తనే సొంతంగా లింకన్ పట్టణంలో ఓ బడి పెట్టాడు. అప్పుడు జార్జ్ బూల్ వయసు 19 ఏళ్ళు మాత్రమే! తన సొంత బడి కాబట్టి బూల్ విద్యాబోధనలో అనేక ప్రయోగాలు చేశాడు. భాషాబోధన, గణితశాస్త్ర బోధనల మీద ఆరోజుల్లోనే ఒక వ్యాసం రాశాడు. వేరే భాషలో పదాలూ, వ్యాకరణ సూత్రాలూ వల్లె వేస్తే వచ్చే చదువు వలన మనోవికాసం కలగదనీ, ఆభాషలో మాట్లాడి, ఆ సాహిత్యాన్ని చదవాలనీ ఉద్బోధించాడు. పాతసాహిత్యంలో ఉన్న హేయమైన విషయాలని వదిలి నీతిదాయకమైన వాటిని మాత్రమే బోధించాలనీ చెప్పాడు. ఏదైనా అర్థం కాకుండా బట్టీ వెయ్యకూడదని నిర్దేశించాడు. మంచీ చెడుల విచక్షణ, నిజాయితీ, కష్టపడి పని చెయ్యడం, పవిత్రమైన వాటిని గౌరవించడం – ఇవన్నీ పిల్లలని గుణవంతులుగా తీర్చిదిద్దుతాయనీ, అవి చదువులో పెద్ద భాగమనీ, ఉపాధ్యాయుడిగా తన బాధ్యత ముఖ్యమయినదనీ గుర్తించాడు. ఆరోగ్యాన్ని కూడా నిర్లక్ష్యం చేసి పనిచేశాడు. బూల్‌కీ, అతని బడికీ చుట్టుపక్కల మంచి పేరొచ్చింది.

సామాజికసేవ

దుర్భరమైన పరిస్థితులనుండి వచ్చినవాడు కనుక, బూల్ ఇబ్బందుల్లో ఉన్న ఇతరులకి సాధ్యమయినంత సాయం చేశాడు. అప్పట్లో లింకన్ పట్టణంలో చాలా వేశ్యాగృహాలుండేవి. సమాజంలో మోసపోయి వేశ్యావృత్తిలోకి దిగిన క్రింద తరగతి స్త్రీల కోసం “ప్రాయశ్చిత్త గృహం” ఒకటి పెట్టి వాళ్ళకి నీడ కలిపించాడు. “మెకానిక్ సంస్థ” (Mechanics Institute) అనే వయోజన కార్మిక విద్యాకేంద్రానికి ట్రస్టీగా పనిచేశాడు. బూల్ ఆ సంస్థ గ్రంథాలయానికి అనేక గ్రంథాలని తెప్పించాడు. స్త్రీలకి అందులో ప్రవేశం ఉండేటట్లు చూశాడు. తీరిక వేళల్లో అక్కడ పాఠాలు చెప్పేవాడు.

ఈ సమయంలోనే బూల్ మంచి ఉపన్యాసకుడిగా కూడా పేరు తెచ్చుకున్నాడు. ఇరవై ఏళ్ళు నిండీ నిండకుండా, హైస్కూలు చదువు కూడా పూర్తి చెయ్యని బూల్, ప్రపంచంలోనే అగ్రగణ్యుడనిపించుకున్న న్యూటన్ పరిశోధనల మీదా, అతని మార్గం లోని లోటుపాట్ల మీదా సాధికారంగా మాట్లాడాడు. అదీ బూల్ వ్యక్తిత్వం – సత్యాన్వేషణలో పెద్దపెద్దవాళ్ళని కూడా సహేతుకంగా విమర్శించడానికి వెనుకాడడు. లింకన్ పట్టణం చుట్టుప్రక్కల వాళ్ళకి బూల్ అసామాన్యుడని గాఢమైన నమ్మకం ఏర్పడింది. 1847 లో, లింకన్‌ పట్టణంలో, ఒక సంస్థ (Lincoln Early Closing Association) కృషి ఫలితంగా ఊళ్ళో దుకాణాలన్నీ పది గంటలకన్నా ఎక్కువ తెరిచి ఉంచమని యజమానులు వాగ్దానం చేశారు. ఆ సందర్భంలో బూల్ “తీరిక సమయం, సద్వినియోగం” (The Right Use of Leisure) అన్న ఒక ఉపన్యాసం ఇచ్చాడు. సృష్టికర్త ఇచ్చిన వైవిధ్యమైన మానవమేధని తదనుగుణంగా అనేక రంగాల్లో వాడి పూర్ణ జీవితాన్ని సాధించాలనీ, ఆట పాటలు, చదువు, సంఘ సేవ, సైన్సు-మతాల మధ్య ఉండాల్సిన సామరస్యం గురించి గంటకి పైగా అనర్గళంగా ఉపన్యసించి ఆకట్టుకున్నాడు.

బూల్ ఇవి సాగిస్తూనే ఖాళీ సమయాల్లో సొంతంగా గణిత శాస్త్రాన్ని అభ్యసించసాగాడు. 1838లో, ఇరవై మూడేళ్ళ వయసులో, బూల్ గణితశాస్త్రంలో మొదటి పేపర్ ప్రచురించాడు. డంకన్ గ్రెగరీ (Duncan Gregory) అనే గణితశాస్త్రవేత్త “కేంబ్రిడ్జ్ జర్నల్” అన్న గణితశాస్త్ర జర్నల్‌కి సంపాదకుడిగా ఉండేవాడు. బూల్ మట్టిలో ఉన్న మాణిక్యమని గ్రెగరీ గ్రహించాడు. గ్రెగరీ బూల్‌కి పేపర్లు ఎలా రాయాలో సలహా లిచ్చాడు. తద్వారా బూల్ కి గణిత ప్రపంచంతో సంబంధాలేర్పడ్డాయి. గ్రెగరీ బూల్‌ని తను సొంతంగా చదివిన చదువు చాలదనీ, గణితశాస్త్రంలో పట్టా పొందమనీ ప్రోత్సహించాడు. కానీ, బూల్ తల్లిదండ్రులని వదిలి వెళ్ళలేక, బడిమీద వచ్చే ఆదాయాన్ని వదులుకునే ఆర్థిక స్వాతంత్ర్యం లేక నిస్సహాయుడై యూనివర్సిటీకి వెళ్ళలేకపోయాడు. (ప్రపంచ ప్రఖ్యాత భారతదేశ గణితశాస్త్రవేత్త శ్రీనివాస రామానుజన్ కూడా ఏ డిగ్రీలూ లేకుండా స్వతహాగా నేర్చుకొని ప్రతిభ కనబరచాడు. హార్డీ చొరవ తీసుకొని రామానుజన్‌ని ప్రోత్సహించి కేంబ్రిడ్జికి తీసుకురాకపోతే రామానుజన్ పేరు గణితశాస్త్ర చరిత్రలో ఉండేది కాదేమో!) కానీ, బూల్ క్రుంగిపోకుండా సొంత పరిశోధనలమీద దృష్టి కేంద్రీకరించాడు. సాధ్యమైనంత వరకు గణిత శాస్త్రవేత్తలతో ఉత్తరప్రత్యుత్తరాలు సాగించాడు. 1844లో ప్రచురించిన “On a General Method in Analysis” అన్న పేపరుకి రాయల్ సొసైటీ వాళ్ళు బంగారు పతకాన్నివ్వడంతో బూల్ కి గణిత ప్రపంచంలో పేరొచ్చింది. 1847లో బూల్ “The Mathematical Analysis of Logic, being an Essay Towards a Calculus,” అన్న చిన్న పుస్తకాన్ని ప్రచురించాడు. ఇది గణితంలో విప్లవాత్మకమైన మార్పులని తీసుకొచ్చింది. అయితే, దీనిని తొందరపడి రాశానని బూల్ తరవాత భావించాడు. ఆ భావాలనే మళ్ళీ 1854లో విపులంగా ప్రచురించాడు. వాటి లోతుల్లోకి వెళ్ళే ముందు బూల్ జీవితంలో వచ్చిన మరికొన్ని మార్పులని చూద్దాం.

1846 నాటికి బూల్ కి తన బడిపంతులు జీవితంపై అసహనం పెరిగింది. గణితంలో మౌలికమైన పరిశోధనలు చెయ్యగలననే నమ్మకం ఏర్పడింది. అందుకు సరయిన వాతావరణం మంచి యూనివర్సిటీలో ఉద్యోగం. కానీ, బూల్ సాంఘికస్థాయి వలన, సరైన డిగ్రీ లేకపోవడం వలన ఇంగ్లాండులో ఎక్కడా ఉద్యోగం రాలేదు. విచిత్రంగా ఇంగ్లాండు పాలిస్తున్న ఐర్లండులో ఓ అవకాశం వచ్చింది!

ఐర్లండులో క్యాథలిక్కులు, ప్రొటెస్టంటులూ ఉన్నా, ఐర్లండులో ఉన్న ఒకే ఒక్క యూనివర్సిటీ ప్రొటెస్టంట్లకు అనుకూలంగా ఉండేది. క్యాథలిక్కులు తమకూ యూనివర్సిటీలు కావాలని ఆందోళన చేశారు. అందుకు తలవొగ్గిన బ్రిటిషు ప్రభుత్వం మూడు కొత్త యూనివర్సిటీలని పెట్టింది – అయితే అవి ఏమతానికీ ప్రాతినిధ్యం ఇవ్వవని తీర్మానించింది. వాటిలో ఒకటయిన క్వీన్‌స్ కాలేజీ (Queen’s College in Cork, Belfast) లో బూల్ 1849 లో, 34 ఏళ్ళ వయసులో గణితశాస్త్ర అధ్యాపకుడిగా చేరాడు. ఎట్టకేలకు బూల్ తన మేధాశాక్తిని సరిగా ఉపయోగించుకునే వాతావరణంలోకి ప్రవేశించాడు.

1845 నుండి 1852 దాకా ఐర్లండు ఘోరమైన కరువు (Irish Potato Famine) నెదుర్కొంది. బంగాళాదుంప పంట పురుగుపడి నాశనమయిపోవడంతో దాని మీద ఆధారపడిన లక్షలాది పేద ప్రజలు అల్లాడిపోయారు. ఐర్లండుని పాలిస్తున్న బ్రిటీషు ప్రభుత్వ అసమర్థత వలన ప్రజలకి తిండికి గతిలేకపోయింది. పది లక్షల మంది ప్రజలు జబ్బు వల్లా, ఆకలి వల్లా చనిపోయారు; అయిదు లక్షల మంది వేరే దేశాలకి వలసపోయారు. కానీ, అటువంటి పరిస్థితులలో ఐర్లాండు వచ్చిన బూల్ స్థానిక ప్రజల కష్టాల గురించి పెద్దగా స్పందించిన ఆధారాలు కనబడవు. దానికితోడు, గుర్రాలనీ గాడిదలనీ సరిగా చూడటం లేదని వాపోతూ, జంతువుల మీద ప్రేమ చూపెడుతూ బూల్ పేపర్లకి ఉత్తరాలు రాయడం చూస్తే ఆశ్చర్యం కలుగుతుంది. మృదు స్వభావానికి మారుపేరనిపించిన బూల్ జీవితంలో ఇదొక పెద్ద మచ్చగానే కనిపిస్తంది.

ఐర్లండులో ఒక యూనివర్సిటీ ప్రొఫెసరు తన మేనకోడలు మేరీ ఎవరెస్టుని బూల్ కి పరిచయం చేశాడు. (ఆమె బాబాయి బ్రిటిషు సర్వేయరు కల్నల్ సర్ జార్జ్ ఎవరెస్టు. ఇతని గౌరవార్థమే ఎవరెస్టు శిఖరానికా పేరు పెట్టారు.) మేరీ కి గణితంలో ఆసక్తి ఉంది. బూల్ ఆమెకు ప్రైవేట్లు చెప్పాడు. ఇద్దరూ దగ్గరయారు. అయిదేళ్ళ తర్వాత హఠాత్తుగా తండ్రి చనిపోవడంతో మేరీ ఆర్థికమైన చిక్కుల్లో పడింది. బూల్ ఆమెను వివాహం చేసుకోదలచాడు. 1855 లో పెళ్ళయేనాటికి బూల్ వయసు 40, మేరీ వయసు 23 మాత్రమే.

మేరీ బూల్
Courtesy of Agness Scott College

మేరీలో బూల్‌కి అనుకూలమైన జీవిత సహచారిణి దొరికింది. వాళ్ళ దాంపత్య జీవితం సంతోషంగా గడచింది. అయిదుగురు ఆడపిల్లలు కలిగారు. అయితే పెళ్ళయిన తొమ్మిదేళ్ళకి, 1864 నవంబరు 24వ తేదీన, తన 49వ ఏట బూల్ అర్థాంతరంగా న్యుమోనియా బారిన పడి, సరైన సమయానికి వైద్య సహాయం అందక మరణించాడు. బూల్ చనిపోయిన తరువాత మేరీ బూల్ విద్యా బోధన గురించీ, ముఖ్యంగా, గణితశాస్త్ర బోధన గురించీ ఎన్నో పుస్తకాలు రాసింది. తన అయిదుగురు పిల్లలనీ విశిష్ట వ్యక్తులుగా తీర్చి దిద్దింది. మేరీ బూల్ 84 ఏళ్ళ వయసులో, 1916లో మరణించింది. జార్జ్, మేరీల సంతానంలో మూడవది అయిన అలీషియా (Alicia Boole Scott) కూడా తండ్రిలాగే గణితశాస్త్రంలో ఎంతో పరిశోధన చేసి పేరు పొందింది.

వివాదంలో రూపొందిన కొత్త బీజగణితం

అనాదిగా భారతీయులు బీజగణితంలోనూ, గ్రీకులు రేఖాగణితంలోనూ ముందుండేవారనీ కిందటి సంచికలో లైబ్నిజ్ వ్యాసంలో తెలుసుకున్నాం. యూరోపియన్లు పదిహేనో శతాబ్దందాకా విజ్ఞానాంధకారంలో ఉన్నా బీజ, రేఖా గణితాలు నేర్చుకొని బీజగణితాన్ని రేఖాగణితానికి అన్వయించి ఓ విప్లవం సృష్టించి ముందుకెళ్ళారు. ఆ ఊపుతో యూరప్ ఇక వెనక్కి చూడలేదు. బీజగణితాన్ని మనమందరం చిన్నప్పుడు చదువుకుని ఉంటాము. – పువ్వులెన్ని, తుమ్మెదలెన్ని లాంటి లెక్కల్లో, పువ్వులు X, తుమ్మెదలు Y అనుకొని సమీకరణాలు సాధించి వాటి విలువలు తెలుసుకునే వాళ్ళం. దానికి కొన్ని సూత్రాలు వాడేవాళ్ళం. సంకేతాలు తారుమారయినా తేడా ఉండదని ఒక సూత్రం: (Commutative law) X + Y = Y + X; ఉదా. 2 + 3 = 3 + 2. అలాగే X.Y = Y.X ఉదా. 2 . 3 = 3 . 2. (ఇక్కడ చుక్క గుణకారాని(multiplication)కి గుర్తు. ఆ గుర్తుని తీసేసి రాయడం కూడా మామూలు.)

బూల్ కాలం నాటికి బ్రిటన్ లో కొంతమంది గణిత శాస్త్రజ్ఞులు, ముఖ్యంగా జార్జ్ పీకాక్ (George Peacock) లాంటి వారు, బీజగణితం లో వాడే సంకేతాలు-– X, Y, Z, +, . -– (symbols) ఇవి అంకెలకీ, కూడికలకీ, గుణకారాలకీ మాత్రమే వర్తిస్తాయా లేక ఇతరత్రా వేటికైనా వర్తిస్తాయా అని ఆలోచనలో పడ్డారు. అవి అంకెలకే పరిమితం కానవసరం లేదని తేల్చారు. దీనితో బూల్ కి కూడా తర్కంలో సంకేతాలు వాడి వాటి మీద కొన్ని సూత్రాలని ప్రతిపాదించవచ్చనే ఆలోచన వచ్చింది.

దానికి స్ఫూర్తి స్కాటిష్ తత్వవేత్త హామిల్టన్ (Sir William Hamilton, 9th Baronet), గణిత శాస్త్రవేత్త అగస్టస్ డీ మోర్గన్ (Augustus De Morgan)ల మధ్య వచ్చిన వివాదం. డీ మోర్గాన్ బూల్ కి దగ్గర స్నేహితుడు. డీ మోర్గన్ 1806 లో భారత దేశంలో మధురైలో పుట్టాడు. చిన్నప్పుడే ఒక కన్ను పోగొట్టుకున్నందువల్ల తోటిపిల్ల హేళనకి గురయేవాడు. అందువల్ల ఆటపాటల కన్నా చదువులో ఎక్కువగా నిమగ్నమయి ఉండేవాడు. కేంబ్రిడ్జ్ లో ముందు లా చదివాడు. ఇష్టం లేక దానిని వదిలేసి గణితం అధ్యయనం చేసి జార్జ్ పీకాక్ ప్రభావంలో పడ్డాడు. అయితే మతసంబంధమైన అపనమ్మకాల వలన కేంబ్రిడ్జ్, ఆక్స్‌ఫర్డ్ యూనివర్సిటీలలో ఉద్యోగం రాలేదు. (అప్పట్లో ఆ యూనివర్సిటీల్లో క్రైస్తవులు కానివారికి విద్యార్థిగా కానీ, అధ్యాపకుడిగా కానీ ప్రవేశం లేదు.) అప్పుడు కొత్తగా స్థాపించిన లండన్ యూనివర్సిటీ మత ప్రాతిపదికలకి అతీతంగా ఉండేది. 22 ఏళ్ళ డీ మోర్గన్ అందులో గణిత, తర్కశాస్త్ర అధ్యాపకుడిగా చేరాడు.

హామిల్టన్ తర్కం గురించి కొన్ని ప్రతిపాదనలు చేశాడు. అప్పట్లో తర్కశాస్త్రం అరిస్టాటిల్ తరువాత అంతగా అభివృద్ధి చెందలేదు. అప్పట్లో తర్కం సముదాయాల (sets)కి సంబంధించిన నాలుగు రకాల ప్రతిపాదనలకి మాత్రమే పరిమితమై ఉండేది. హామిల్టన్ వీటికి కొన్ని కొత్తవాటిని కలిపి తర్కశాస్త్ర పరిధిని పెంచడానికి పూనుకున్నాడు. కానీ, హామిల్టన్‌కి గణితశాస్త్రమన్నా, గణితశాస్త్రవేత్తలన్నా చిన్నచూపు. అదే సమయంలో డీ మోర్గన్ తర్కశాస్త్ర లక్షణాలని సంకేతాలద్వారా సూత్రీకరించవచ్చని (Quantification of the predicate) చెప్పాడు. ఇది హామిల్టన్ సూత్రీకరించిన దానికి కొంచెం దగ్గరగా ఉంది. హామిల్టన్ వెంటనే డీ మోర్గన్ గ్రంథచౌర్యం చేశాడని వివాదం లేవదీశాడు. (ఈ ఆరోపణలో నిజం లేదని తరువాత ఋజువయింది.) ఈ వివాదాన్ని పక్కనుండి తిలకిస్తున్న బూల్ వీళ్ళిద్దరి ఆలోచనల్లోని మంచి చెడ్డలని బేరీజు వేశాడు.

హామిల్టన్ కి లెక్కలంటే పడకపోయినా, ఆయన ఆలోచనలకి తగినట్లు సముదాయాలని కలపడానికి సమీకరణాలు వాడి ఉండవచ్చు. డీ మోర్గన్ సంకేతాలని తార్కిక ప్రక్రియలకి వాడటం గజిబిజి వ్యవహారం; కాని సముదాయాలకి సంకేతాలని (symbols) వాడి, సముదాయాల సంబంధాలకి సమీకరణాలు వాడవచ్చనే అమోఘమైన ఆలోచన బూల్‌కి వచ్చింది. ఇక వెంటనే దాని గురించి రాయడం మొదలెట్టాడు. అతి వేగంతో కొద్ది నెలలలోనే దీని మీద పుస్తకం, “The Mathematical Analysis of Logic, being an Essay Towards a Calculus,” రాసి 1847 లో ప్రచురించాడు. (ఈ పుస్తకం, డీ మోర్గన్ రాసిన “ఫార్మల్ లాజిక్” (“Formal Logic”) అన్న పుస్తకం ఒకే రోజున ప్రచురించబడింది.) బూల్ తరవాత దానిని తొందరపడి ప్రచురించానని భావించి, 1854లో “An Investigation of the Laws of Thought, on which Are Founded the Mathematical Theories of Logic and Probabilities” పేరిట సవరించి తన మాస్టర్‌పీస్ ప్రచురించాడు.

కొన్ని వేల సంవత్సరాలుగా గణితశాస్త్రం అంకెలకీ, ఆకారాలకీ (రేఖాగణితంలో త్రిభుజం, చతురస్రం మొదలైనవి)మాత్రమే పరిమితమై ఉండేది. బీజగణితంలో సంకేతాలు వాడినా అవి సంఖ్యలకే వాడతాం. బూల్ కొత్తగా సంకేతాలని వస్తు సముదాయాలకి వర్తించాడు. ఇదే బూల్ బీజగణితానికి నాంది అయింది. దాని వల్ల ఇంతకు ముందు పరిధిలోకి రాని వాటినెన్నిటిగురించో గణితశాస్త్ర పరంగా ఆలోచించే అవకాశం కలిగింది. ఈ కొత్త గణితాన్ని కనుగొన్నవిధం కూడా ఊహించలేనిది – దానికి స్ఫూర్తి నిచ్చింది సాధారణ వాడుక భాష !

ఆలోచనా సూత్రాలు

లైబ్నిజ్ మానవ వివేచనని యాంత్రికం చెయ్యాలని కలుగన్నాడు. బూల్ దీనిని పరిశీలించిన విధం మనల్ని చకితులని చేస్తుంది. మనం మాట్లాడే భాష మన భావాలని వ్యక్తపరచే వాహిక మాత్రమే కాదు – వివేచనకి సాధనం అన్న విషయం అందరూ అంగీకరిస్తారు. భాషకీ గుణం ఎలా వస్తుందో బూల్ ఆలోచించాడో చూద్దాం.

బీజగణితంలో లాగానే, X, Y లాంటి సంకేతాలని మనం ఆలోచించే వాటికి గుర్తుగా పెట్టుకుందాం. అలాగే, +, – గుర్తుల్ని, భావనలని కలపడానికీ, విడదీయడానికీ, కొత్త భావనలని సృష్టించడానికీ వాడదాం. అందమైన వాళ్ళ వర్గం X అనుకుందాం. అంటే, అందమైన ప్రతివాళ్ళూ X అనే వర్గానికి (class) చెందుతారన్నమాట. అమ్మాయిల వర్గాన్ని Y అందాం. కొందరు X వర్గానికీ, కొందరు Y వర్గానికీ చెందుతారు. కొందరు – అందం, ఆడతనం అన్న రెండు గుణాలూ కలవాళ్ళు – ఈ రెండు వర్గాలకీ చెందుతారు. ఆ వర్గాన్ని, అంటే X, Y వర్గాలు రెంటిలోనూ ఉన్న వాళ్ళ వర్గాన్ని, X.Y అని బూల్ సూచించాడు. ఇక్కడ వాడిన చుక్క గుర్తు సంఖ్యలతో చేసే గుణకారానికి వాడే (X కి బదులు) చుక్క లాంటి గుర్తు. ఒక్కొక్కప్పుడు ఆ గుర్తుని వదిలేసి XY అని రాస్తారు. కానీ, ఇక్కడ చేస్తున్నది గుణకారం కాదు, ఈ వర్గానికీ, ఆ వర్గానికీ చెంది ఉన్న వారిని సూచించడానికి వాడే సంకేతం.

అదే విధంగా, అమ్మాయిల్లో అందమైన వాళ్ళు అన్న వర్గానికి సంకేతం YX. ఈ రెండు వర్గాలూ సమానమే కదా. ఇది ఏ సూత్రాన్ని తెలుపుతుంది? XY = YX. ఇది మనం అంకెలతో చేసే గుణకార సూత్రం – సంకేతాలని తారుమారు చేస్తే తేడా ఉండదన్న (ఉదా: 2 x 3 = 3 x 2)సూత్రం లాంటిదే! దీనిని అంకగణితంలో (Arithmetics) కామ్యుటేటివ్ లా (Commutative Law) అంటారు. కానీ, గుణకారానికీ, దీనికీ ఓ ముఖ్యమైన తేడా ఉంది. Y అమ్మాయిల వర్గాన్ని సూచిస్తే, YY దేనిని సూచిస్తుంది? అమ్మాయిల అమ్మాయిల వర్గం! అమ్మాయిలు, అమ్మాయిలు అన్నా, వట్టి అమ్మాయిలన్నా ఒకటే గదా! అంటే, YY = Y. అంకగణితంలో ఏ సంఖ్యనైనా దానితో హెచ్చిస్తే అదే వస్తుందా? 5 x 5 = 25 కాని 5 కాదు. అయితే ఒక్క క్షణం ఆగండి. 1 x 1 = 1, 0 x 0 = 0! అంటే, కొత్త గణితంలో “0”, “1” అన్న రెండే రెండు సంఖ్యలుంటే అప్పుడు మన బీజగణిత సూత్రాలు ఈ కొత్త గణితానికీ వర్తిస్తాయి!

మనం ఇక్కడ వర్గాల గురించి మాట్లాడుకుంటున్నాం కదా, మరి ఆ సందర్భంలో 0, 1 లకి అర్థం ఏమిటి? బూల్ “0” శూన్య వర్గాన్నీ, “1” విశ్వవర్గాన్నీ సూచిస్తాయన్నాడు. వాటి అర్థం : శూన్య వర్గంలో ఏదీ ఉండదు. విశ్వవర్గంలో ఉండనిదేదీ లేదు. సామాన్య బీజగణితంలో ఉన్న “+”, “-” (కూడిక, తీసివేత) సంకేతాలకి కూడా బూల్ బీజగణితంలో ఇలా అర్థం చెప్పుకోవచ్చు. X+Y వర్గంలో X వర్గం వాళ్ళూ, Y వర్గం వాళ్ళూ అందరూ ఉంటారు. పై ఉదాహరణ ప్రకారం, X+Y వర్గంలో అందమైన వాళ్ళూ, అమ్మాయిలూ ఉంటారు. ఉన్న ప్రతివాళ్ళూ అందమైన వాళ్ళు కాదు, ప్రతివారూ అమ్మాయి కానవసరం లేదు. అమ్మాయైనా అయి ఉండాలి లేదా అందమైనదైనా అయి ఉండాలి. అమ్మాయి కానివారు మాత్రం అందమైన వాళ్ళయి ఉండాలి. సామాన్య గణితంలో లాగానే ఇక్కడా, X, Y లని తారుమారు చెయ్యొచ్చు : X+Y = Y+X. Z పొడవైనవాళ్ళ వర్గాన్ని చూచిస్తే, Y-Z అన్నది పొడుగుకాని అమ్మాయిల వర్గాన్ని సూచిస్తుంది. 1 అన్నది విశ్వ వర్గాన్ని సూచిస్తుంది కనుక, 1 – Y, అమ్మాయిలు కాని వాళ్ళని, అంటే అబ్బాయిలని సూచిస్తుందన్నమాట. అమ్మాయిలూ, అమ్మాయిలు కాని వాళ్ళూ, అంటే, Y + (1-Y) ఎవర్నిసూచిస్తుంది? అందర్నీ, అంటే విశ్వవర్గాన్ని సూచిస్తుంది. Y + (1-Y) = 1 అంటే, అందరూ ఉన్న వర్గం. ఈ సమీకరణాన్ని మనం మామూలు బీజగణితంలో సాధించినట్లే (Y నీ -Y నీ ఒకదాన్నొకటి కొట్టెయ్యడం) గమనించండి.

ఇంకొక్కసారి YY = Y అన్న సమీకరణాన్ని చూద్దాం. దీనినే Y – YY = 0 అనీ Y (1-Y) = 0 అనీ రాయొచ్చు. దీని అర్థం ఏమిటి? Y వర్గానికీ, (1 – Y) వర్గానికీ (అంటే రెండు వర్గాలకీ) చెందినవి శూన్య వర్గం లోనివి – అంటే ఏమీలేని వర్గం. (1 – Y) వర్గానికి చెందడం అంటే, Y వర్గానికి చెందకపోవడం. Y వర్గానికి చెందినదీ, అదే వర్గానికి చెందనిదీ అంటూ ఎక్కడా ఉండదు, అని YY = Y సమీకరణం అర్థం. ఇది బూల్ కి గొప్ప ఉత్సాహాన్నిచ్చింది. ఎందుకంటే అరిస్టాటిల్ తత్వశాస్త్రంలోకెల్లా ముఖ్యమైనదంటూ ప్రతిపాదించిన ప్రాథమిక సూత్రం ఇదే – ఏదయినా ఓ గుణాన్ని పొందీ పొందకపోవడం అసంభవం, అటో ఇటో తేలాలి. దీనినే “వైరుధ్య నియమం” (Principle of Contradiction) అంటారు. బూల్ తన సూత్రాలతో దానినే నిర్థారించాడు.

శాస్త్రజ్ఞులు కొత్త సిద్ధాంతాలు చేసినప్పుడు వాటిని ఉపయోగించి అంతకు ముందే సర్వత్రా అంగీకరీంచిన సిద్ధాంతాలని ఋజువు చేస్తే ఆ సిద్ధాంతం మీద గురి పెరుగుతుంది. అది కనుక్కున్న వాళ్ళకి ఉత్సాహమూ, ప్రోత్సాహమూ కలుగుతాయి. అరిస్టాటిల్ నియమాన్ని తన సిద్ధాంతం సులభంగా ఋజువు చేసినందుకు బూల్ ఎగిరి గంతేసి ఉండాలి.

అరిస్టాటిల్ కాలం నుంచీ తర్కంలో పెద్ద మార్పేమీ లేదు. దానినే అందరూ శిరోధార్యమన్నారు. బూల్ వచ్చి అరిస్టాటిల్ తర్కమంతా ఈ కొత్త బీజగణితంలో ఓ చిన్న భాగం మాత్రమేనని నిరూపించాడు. ఉదాహరణకి, “మానవులు మర్త్యులు”, “సోక్రటిస్ మానవుడు”, “కావున సోక్రటీస్ మర్త్యుడు” అన్న తర్కవాదం ( syllogism )మనందరికీ తెలుసు. ఇప్పుడు దీనిని బూల్ గణితంలో సులభంగా సమీకరణాల ద్వారా నిరూపిద్దాం. మానవుల వర్గాన్ని X, మర్త్యుల వర్గాన్నిY అందాం. X లోని ప్రతిదీ Y లో ఉంటుంది. అంటే X లో ఉండి Y లో లేనిదేదీ లేదు : X (1-Y) = 0. దానిని విస్తరించి రాస్తే, X –XY = 0 లేదా X = XY అని రాయొచ్చు. సోక్రటీస్ వర్గాన్ని Z అందాం. X మానవ వర్గాన్ని సూచిస్తుంది కనుక, 1 – X అన్నది మానవులు కాని వర్గాన్ని సూచిస్తుంది. సోక్రటీస్ ఆవర్గానికి చెందడు కనుక, Z (1-X) = 0. దానిని విస్తరిస్తే, Z – ZX = 0, లేదా, Z = ZX అవుతుంది. పైన, X = XY అని చూపించాం, X బదులు XY రాస్తే, Z = ZXY = (ZX)Y = ZY అవుతుంది. దీనినే Z(1-Y) = 0, అంటే సోక్రటిస్ మర్త్యులు కాని వర్గానికి చెందడు, సోక్రటీస్ మర్త్యుడు అని నిరూపించాం! “ఇది డొంక తిరుగుడుగా ఉందే!” అని మీకనిపించవచ్చు. కానీ, తర్క సంబంధమైన విషయాలని బీజగణితంలో లాగా సమీకరణాల ద్వారా సాధించగలిగాం. అందుకు కొన్ని సూత్రాలని వాడుకున్నాం. ఈ సూత్రాలని ఇంకా ఎన్నో క్లిష్టమైన సమస్యలని యంత్రబద్ధంగా సాధించడానికి వాడుకోవచ్చు. అదీ బూల్ గణితంలోని మహత్తు!

వర్గాలతో సాధించినదాన్నే, బూల్ ప్రతిపాదనలకి గూడా వర్తించాడు. వర్గాలలో 0, 1 లు వరుసగా శూన్య, విశ్వ వర్గాలనిసూచిస్తే, ప్రతిపాదనలలో 1, 0 వరుసగా సత్య, అసత్యాలని సూచిస్తాయి. ప్రతిపాదన X నిజమయితే దానిని X = 1 అనీ, కాకపోతే X = 0 అనీ సమీకరణాలని వాడి రాయచ్చు. X.Y (అంటే X AND Y), లేక చుక్కగుర్తుని వదిలేస్తే వచ్చే, XY ప్రతిపాదన ఎప్పుడు నిజమవుతుంది? X, Y, రెండూ నిజమయినప్పుడే కదా! అంటే, 0.0 = 0 ; 1.0 = 0 ; 0.1 = 0 ; 1.1 = 1. ఇది అంకగణితంలోని గుణకారం లా ఉందని గ్రహించండి. అలాగే, X+Y (అంటే X లేదా Y) అన్న ప్రతిపాదన ఎప్పుడు నిజమవుతుంది? X, Y – రెండు ప్రతిపాదనలలో ఏ ఒక్కటి నిజమయినా చాలు, X + Y నిజమవుతుంది: 0 + 0 = 0 ; 1 + 0 = 1 ; 0 + 1 = 1 ; 1 + 1 = 1. ఇది అంకగణితంలోని కూడికలా ఉంది. 1 + 1 = 1, అన్నది మాత్రం కొత్తగా ఉంది. అయితే, 1 సత్యాన్ని సూచిస్తుందనీ, సత్యం + సత్యం = సత్యం అన్నది సబబేనని ఒప్పుకుంటాం.

ఒక ప్రతిపాదన X నిజమయితే, దానిమీద ఆధారపడిన వేరే ప్రతిపాదన Y కూడా నిజమయితే (X నిజమయితే Y నిజం – if X then Y అన్నదాన్ని) X(1-Y)=0 అని సూచించవచ్చు. దీనిని ఇలా అర్థం చేసుకోవచ్చు: X సత్యమయి, Y అసత్యమవడం అన్నది అసత్యం – X సత్యమయితే, Y కూడా సత్యం కావాల్సిందే.

ఈ సూత్రాలతో వివేచనని, కనీసం కొన్ని సందర్భాలలోనయినా, సమీకరణాలని సాధించినట్లుగా యాంత్రికంగా చెయ్యొచ్చు. ఉదాహరణకి, “మబ్బులు క్రమ్మితే వర్షం పడుతుంది”, “వర్షం పడితే గొడుగు అవసరం” అన్న ప్రతిపాదనలని తీసుకుందాం. మబ్బులు క్రమ్మడాన్ని X గా, వర్షం పడటాన్ని Y గా, గొడుగు అవసరాన్ని Z గా గుర్తించుదాం. అప్పుడీ ప్రతిపాదనలని X(1-Y) = 0, Y(1-Z) = 0 సమీకరణాలగా రాయొచ్చు. మబ్బులు క్రమ్మాయన్నది నిజమని మనకు తెలిస్తే, X=1. దానిని మొదటి సమీకరణంలో X బదులుగా వాడి Y=1 అనీ, దానిని రెండో సమీకరణంలో Y బదులుగా వాడి, Z=1 అనీ సులభంగా చూపెట్టవచ్చు. అంటే గొడుగు అవసరం అని తేల్చాము!

ఈ చిన్న ఉదాహరణలు డొంకతిరుగుడుగా అనిపించినా, వివేచనని సమీకరణాలతో సాధించడమన్నది విప్లవాత్మకమైన విషయం. ఈ కొత్త గణితాన్ని సంకీర్ణమైన వివేచనకి కూడా అన్వయించవచ్చునన్న ఆశ శాస్త్రజ్ఞులకి కలిగించింది. కానీ, బూల్ పుస్తకంలో ఎక్కడా కంప్యూటింగ్ యంత్రాల ప్రసక్తే లేదు. బూల్ సమకాలికుడైన బాబేజ్‌ బూల్ గణిత ప్రాముఖ్యాన్ని గుర్తించాడు కానీ, అది కంప్యూటింగ్‌కి ఎలా పనికొస్తుందో గ్రహించలేదు. తరువాత కొన్నేళ్ళకి బెర్ట్రాండ్ రస్సెల్ (Bertrand Russell)ఇది ప్యూర్ మేథమేటిక్స్ (Pure Mathematics) కి నాంది పలికిందని బూల్‌ని కొనియాడాడు. బూల్ చనిపోయిన డెబ్భై ఏళ్ళకి “క్లాడ్ షానన్” అనే ఓ అమెరికన్ ఇంజనీరింగ్ విద్యార్థి పుణ్యమా అని ఈ కొత్త గణితాన్ని నిత్యజీవితంలో వాడటం మొదలెట్టాం.

బూల్ సూత్రాలనీ ఎలెక్ట్రిక్ సర్క్యూట్లనీ అనుసంధానించిన విద్యార్థి

క్లాడ్ షానన్ (Claude Shannon) అమెరికాలోని మిచిగన్ రాష్ట్రంలో 1916 లో పుట్టాడు. చిన్నప్పటి నుండీ కదిలే ఆటవస్తువులంటే ఇష్టం. ఇంట్లో రేడియోలనీ ఇతర వస్తువులనీ పీకి పందిరేసే వాడు. వాటితో పాటు లెక్కలంటే చాలా ఆసక్తి. షానన్ యూనివర్సిటీ ఆఫ్ మిచిగన్ లో గణితంలో, ఎలెక్ట్రికల్ ఇంజనీరింగ్‌లో డిగ్రీలు సంపాదించాడు. మాస్టర్స్ చేయడానికి ఎం.ఐ.టీ.(Massachusetts Institute of Technology)కి వెళ్ళాడు. అక్కడ వానెవర్ బుష్ (/Vannevar Bush) అన్న ప్రొఫెసరు దగ్గర రిసెర్చ్ అసిస్టెంటుగా చేరాడు.

అనలాగ్ కంప్యూటర్

గణితం, యాంత్రికశాస్త్రం (Mechanics) రెండూ బుష్ అభిమాన విషయాలే. బుష్ అప్పట్లో ఓ పెద్ద అనలాగ్ (analog) కంప్యూటర్ ని తయారుచేశాడు. మనం ఇప్పుడు వాడేవన్నీ డిజిటల్ కంప్యూటర్లు. అనలాగ్ కంప్యూటర్లు భౌతికమార్పుని – వేగం, దూరం లాంటి వాటిని – కొలవడం ద్వారా కంప్యుటేషన్ చేస్తాయి. దీంట్లో చక్రాలూ, గేర్లూ, వీటిని కలిపే కడ్డీలూ, వాటిని తిప్పే మోటార్లూ ఉంటాయి. కిందటి సంచికలో లైబ్నిజ్ మీద రాసిన వ్యాసంలో సమాకలన, అవకలన గణితం (Integral and DIfferential Calculus) గురించి తెలుసుకున్నాం. ఒకటి తాత్కాలిక వేగాన్నీ, వేరొకటి వంపు క్రింద వైశాల్యాన్నీతెలుసుకోడానికి ఉపకరిస్తాయనీ, ఈ రెంటికీ అవినాభావ సంబంధమున్నదనీ తెలుసుకున్నాము. ఇంజనీరింగ్ లో చాలా సమస్యలని అవకలన సమీకరణాల (differential equations) ద్వారా సాధిస్తారు. ఉదాహరణకి, ఇంజనీర్లు ఓ వంతెన కట్టేముందు అది పెనుగాలి కెలా ఊగుతుందో కనుక్కోవాలనుకుంటారు. అందుకు కొన్ని అవకలన సమీకరణాలని రాస్తారు. అనలాగ్ కంప్యూటర్ లోని గేర్లనీ కడ్డీలనీ ఈ సమీకరణాలకి అనువుగా అమర్చి యంత్రాన్ని ఆన్ చేస్తే, కొంత సేపటికి సమీకరణానికి సమాధానాన్ని గ్రాఫు ద్వారా సూచిస్తుంది.

అనలాగ్ కంప్యూటర్‌తో వానెవర్ బుష్

అలాగే ఓ పెద్ద భవనం కట్టే ముందర, అది భూకంపానికి తట్టుకుంటుందో లేదో తెలుసుకోవాలంటే, మళ్ళీ కొన్ని సమీకరణాలు రాసి, వాటికి తగినట్లు గేర్లని అమర్చి, యంత్రాన్ని ఆన్ చేస్తే, కొంత సేపటికి సమాధానాన్ని గ్రాఫు ద్వారా సూచిస్తుంది. కంప్యూటర్‌కి ఆ సమీకరణాన్ని సాధించడానికి కొన్ని సార్లు గంటలు, రోజులు కూడా పట్టొచ్చు! అప్పట్లో అది చెప్పుకోదగ్గ విషయం. బుష్ తయారు చేసిన యంత్రం బాబేజ్ యంత్రం లాగే గేర్లూ, చక్రాలతో కూడుకొని ఉంది. గేర్లు, చక్రాలు తిప్పడానికి వాడిన విద్యుచ్ఛక్తిని మినహాయిస్తే, ఆనాటి అనలాగ్ కంప్యూటర్ కేవలం మెకానికల్ కంప్యూటర్ మాత్రమే. అట్టహాసంగా, హాలు నింపే ఆ యంత్రం ఫొటోలని బుష్ తో సహా పైన చూడొచ్చు.

సాధించాల్సిన అవకలన సమీకరణాలని బట్టి ఈ యంత్రం గేర్లు సరిగా అమర్చి పెట్టడం చాలా చికాకుతో కూడిన పని. బుష్ ఆ పనిని తన శిష్యుడైన షానన్ కి అప్పగించాడు. షానన్ ఈ కంప్యుటర్‌ని నియంత్రించడానికి ఎలెక్ట్రికల్ సర్క్యూట్లు వాడడానికి ప్రయత్నించాడు. అప్పట్లో చాలా సంకీర్ణమైన సర్క్యూట్లని సరళమైన రిలేల ద్వారా చేసేవాళ్ళు. రిలే అంటే ఓ రకమైన స్విచ్. దాంట్లో ఓ విద్యుదయస్కాంతం ఉంటుంది. దాని గుండా కరెంటు పోయినప్పుడు అది తీగెని లాగి వేరే సర్క్యూట్ని కలుపుతుంది, దాంట్లో కరెంటు ప్రవహిస్తుంది. ఇది పనిచేసే విధానం ఈ బొమ్మలో చూడొచ్చు. ఒక రిలే సర్క్యూట్ మరో రిలే లోని అయస్కాంతాన్ని ప్రభావితం చెయ్యొచ్చు. ఇలా రిలే సర్క్యూట్లని కలిపి సంకీర్ణమైన పెద్ద సర్క్యూట్‌ని తయారుచెయ్యొచ్చు. వాటిని కలిపిన విధానాన్ని బట్టి సర్క్యూట్ లో కరెంటు ప్రవహిస్తుంది. అప్పట్లో టెలెఫోన్ ఎక్స్చేంజ్ లలో ఈ రిలేలతో పెద్ద పెద్ద సర్క్యూట్లు చేసేవాళ్ళు. మనం ఫోన్ డయల్ చేస్తే ఆటోమాటిక్ గా రిలేలతో అవతల లైన్ కనెక్టు చేసేవాళ్ళు. అలా, చాలా వరకు ఆపరేటర్ల అవసరం తగ్గిపోయింది. ఆ సర్క్యూట్లు చాలా పెద్దవి కావడంతో అవి పనిచేసే విధానం అంతుపట్టని సమస్యగా తయారయింది. షానన్ ఈ ఇంజనీరింగ్ సమస్యని గణితపరంగా సాధించాలని ప్రయత్నం చేశాడు.

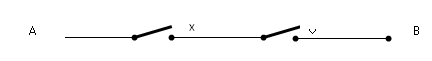
క్రమంగా కలిపిన సర్క్యూట్

ప్రత్యేకమైన సాంకేతికజ్ఞానమూ, సార్వత్రికమైన గణితజ్ఞానమూ మేళవించుకున్న మేధావి షానన్. స్విచ్ ఆన్ అయి ఉన్న స్థితిని 1 తో ఆఫ్ స్థితిని 0 తో సూచించాడు. ఇప్పుడు రెండు స్విచ్ లని కలుపుదాం. వాటిని రెండు విధాలుగా కలపవచ్చు – క్రమంగా (in series), సమాంతరంగా (in parallel). క్రమంగా కలిపితే ఇక్కడ చూపిన విధంగా ఉంటుంది.

ఈ సర్క్యూట్లో A నుండి B కి పోయే మార్గంలో రెండు స్విచ్ లున్నాయి, X, Y. అవి రెండూ ఆన్ అయితే గాని A నుండి B కి కరెంట్ పోదు. ఈ స్విచ్ ల కలయికని X.Y (దీనినే X AND Y అని పిలుస్తారు) గా సూచిస్తే, సర్క్యూట్ ఆన్ అవుతుందా లేదా అన్నది ఈ సులభమైన సూత్రాల ద్వారా తెలుసుకోవచ్చు: 0.0=0 ; 0.1=0 ; 1.0=0 ; 1.1=1. ఇది మన మామూలు లెక్కల్లో గుణకారంలా ఉందని గ్రహించండి. రెండు స్విచ్ లని సమాంతరంగా కలిపితే క్రింది విధంగా ఉంటుంది.

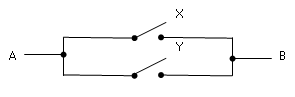
సమాంతరంగా కలిపిన సర్క్యూట్

స్విచ్ లలో ఏ ఒక్కటి ఆన్ అయినా AB మార్గం ఆన్ అయి ఉంటుంది. ఈ సర్క్యూట్ని X+Y (దీనినే X OR Y అని పిలుస్తారు) గా సూచించవచ్చు : 0+0=0; 1+0=1; 0+1=1; 1+1=1. ఈ సమీకరణాలు కూడా మన మామూలు లెక్కల్లో ఉన్నట్లే ఉన్నాయి – చివరిది తప్ప. అది 1+1=1. షానన్ కి తను డిగ్రీలో చదివిన తర్కం గుర్తుకొచ్చింది. బూల్ కనిపెట్టిన బీజగణితంలో 1+1=1 అని పైన తెలుసుకున్నాం.

ఇలా బూల్ బీజగణితాన్నీ ఎలెక్ట్రిక్ సర్క్యూట్లకి అన్వయించడంతో, ఎంత క్లిష్టమైన సర్క్యూట్ నయినా, సమీకరణాల ద్వారా సూచించి, అవి ఎలా పనిచేస్తాయో వివరించే అవకాశం కలిగింది. అంతే కాదు, మనమేదైనా తార్కిక సమస్యని సాధించాలనుకుంటే, దానిని సమీకరణలతో సూచించి, సులభతరం చేసి, వాటిని సర్క్యూట్లుగా మార్చవచ్చు. ఆ విధంగా తార్కిక సమస్యలకీ ఎలెక్ట్రిక్ సర్క్యూట్లకీ మెలిపెట్టిన మేధావి షానన్. దీనిని షానన్ 1937లో తన సిద్ధాంత వ్యాసంలో (Masters thesis) లో వివరించాడు. ప్రస్తుత డిజిటల్ కంప్యూటర్లన్నీ ఈ స్విచింగ్ సర్క్యూట్ ల ఆధారంగానే పనిచేస్తాయి. మనం వాడే కంప్యూటర్లో కొన్ని కోట్ల స్విచ్‌లు (సిలికాన్ మహాత్మ్యం వలన) అనేక విధాలుగా కలిసిఉంటాయి. అవన్నీ బూల్ కనిపెట్టిన బీజగణితం ఆధారంగానే పని చేస్తాయి!

షానన్ ఎం.ఐ.టీ. తరవాత బెల్ ల్యాబ్‌స్‌కి వెళ్ళి విప్లవాత్మకమైన సమాచార సిద్ధాంతాన్ని (Information Theory) కనుగొన్నాడు. పాటలు, ఫొటోలు, పేపర్లు – ఇలా ఎన్నెన్నో రకాలుగా లభించే సమాచారాన్ని కేవలం రెండు సంకేతాలతో, “0”, “1” లతో సూచించవచ్చని ప్రతిపాదించాడు. మనం నిత్యం వాడే సిడీలు, డివిడీలు, కంప్యూటర్లు, ఇంటర్నెట్ – ఇవేవీ షానన్ సమాచార సిద్ధాంతం లేకుండా సాధ్యం కావు. ఆయన 2001 లో, 84 ఏళ్ళ వయసులో మరణించాడు.

ముగింపు

క్లాడ్ షానన్

బీజగణితాన్ని రేఖా గణితానికి అన్వయించి దేకార్త్ (Descartes) యూరప్ విజ్ఞానయుగంలో పురోగమించడానికి కారకుడయ్యాడు. బూల్ బీజగణితాన్ని తర్కానికి అన్వయించి కొత్త గణిత శాస్త్రానికే పునాది వేశాడు. ఆ కొత్త గణితాన్ని ఎలెక్ట్రికల్ ఇంజనీరింగ్ కి అన్వయించి కంప్యూటర్ విప్లవానికి నాంది పలికాడు షానన్. “నా ప్రతిభేమీ లేదు, తర్కమూ, ఇంజనీరింగూ రెండూ చదివి ఉండటం నాకు కలిసొచ్చింది”, అని చాలా తేలిగ్గా తీసిపారేశాడు షానన్ . ఒకదానికొకటి సంబంధం లేని పాయలుగా ఉన్న విజ్ఞానశాఖల్ని, ఎవరో మేధావి వచ్చి కలిపి అనూహ్యమైన రీతిలో ప్రగతి సాధించడం మనకి చరిత్రలో పదే పదే కనిపిస్తుంది.

ఈ వ్యాసంలో మనం ఒక్కసారిగా ఇరవయ్యో శతాబ్దపు కంప్యూటర్ యుగంలోకి వచ్చేసినా, బూల్‌కీ షానన్‌కీ మధ్యకాలంలో చాలా కథ జరిగింది. మానవ వివేచనకి బూలియన్ తర్కమే ఆధారమైతే, గణితానికి పునాదులు కూడా తర్కంలోనే ఉండాలన్న మీమాంస ఆ కాలంలో మొదలయింది. వచ్చే సంచికలో వెనక్కి వెళ్ళి గణితశాస్త్ర పునాదుల్ని కదిపిన కథేమిటో చూద్దాం.

ఉపయోగపడిన పుస్తకాలు

1. “Boole Turns Logic Into Algebra,” in “The Universal Computer: The Road From Leibniz To Turing”, by Martin Davis. W. W. Norton and Company, 2000. ఈ వ్యాస పరంపరకి ఎంతో ఉపయోగపడిన పుస్తకం.
2. “Geroge Boole: His Life and Work”, by Desmond MacHale. Dublin: Boole Press, 1985. ఇది బూల్ సాధికారిక జీవితచరిత్ర. చదవదగ్గ పుస్తకం.
3. “Men of Mathematics,” by ET Bell. “Complete Independence – Boole,” అన్న అధ్యాయంలో బెల్ తన సామ్యవాద భావాల మూలంగా కొంత వక్రీకరించాడని మెక్‌హేల్ (MacHale) తన పుస్తకంలో ఆరోపించాడు.
4. “Lectures on Ten British Mathematicians of the Nineteenth Century,” by Alexander MacFarlane. 1901-1904 మధ్య లేహై యూనివర్సిటీలో ఇచ్చిన ఉపన్యాసాలు. Peacock, De Morgan, Boole – వీళ్ళ మీద ఉన్న అధ్యాయాలు చదవదగ్గవి.
5. “A Symbolic Analysis of Relay and Switching Cirsuits,” by Claude Shannon. MIT Masters Thesis, 1940. సాంకేతిక చరిత్ర గతినే మార్చివేసిన మాస్టర్స్ థీసిస్ ఇది. దీనిని మీంచిన మాస్టర్స్ థీసిస్ మరొకటి లేదు.
6. “1 + 1 = 1 – a tale of genius,” by Ian Petticrew. బూల్ నీ షానన్ నీ కలిపి వారి పనిని వివరించే వ్యాసం.
7. “Tools for Thought: The History and Future of Mind-Expanding Technology,” (Older Edition) by Howard Rheingold. MIT Press, 2000.
8. “An Investigation of the Laws of Thought,” by George Boole. Cosimo Classic, 2007. ఇది బూల్ మాస్టర్ పీస్. మొదటి అధ్యాయాలు అర్థం చేసుకోవడం కష్టం కాదు. అవి చదివితే బూల్ ఎందుకు మేధావో తెలుస్తుంది.
9. “Endless Frontier: Vannevar Bush, Engineer of the American Century,” by G. Pascal Zachary. The Free Press, 1997. గత శతాబ్దపు మొదటి భాగంలో అమెరికాలో ప్రభుత్వ సలహాదారుగా, ఆటంబాంబు ప్రాజెక్టు ప్రారంభకుడిగా, సైన్సులో ప్రభుత్వపాత్రని రూపొందించిన వాళ్ళలో ప్రముఖుడిగా సాటిలేని ఇంజనీరు వానెవర్ బుష్ జీవిత చరిత్ర.
10. “As We May Think,” by Vannevar Bush. The Atlantic Monthly, July 1945. రెండవ ప్రపంచ యుద్ధంలో సైన్సుని వినాశ ప్రయోజనాలకి వాడుకున్నాం. అలాకాక, దానిని మానవ వికాసానికి వాడుకోవాలని ఆశిస్తూ సైంటిస్టులకి కర్తవ్యాన్ని నిర్దేశిస్తూ రాసిన వ్యాసం. మనం చదివే పుస్తకాలూ, చూసే ఫొటోలూ, రాసుకునే నోట్సూ, అన్నీ దాచుకునే యంత్రాన్ని చవగ్గా చెయ్యొచ్చనీ, అది మనం అడిగిన ప్రశ్నలకి ఠకీ మని జవాబిస్తుందనీ జోస్యం చెప్పి, దానికి మెమెక్స్ అని పేరు పెట్టాడు!