ప్రాచీన తెలుగు కొలమానం
ఆధునిక మెట్రిక్ కొలమాన పద్ధతులు ప్రవేశించకముందు తెలుగు ప్రజలకు ఒక ప్రామాణికమైన కొలమాన పద్ధతి ఉండేదని చాలామందికి తెలియదు. ఘనపరిమాణము, బరువు, పొడవు కొలవడానికి తెలుగు వారు చారిత్రకంగా వాడుకున్న కొలమాన పద్ధతులను, ఇందు నిమిత్తం ఉపయోగించిన పదాలను, చిహ్నాలను స్థూలంగా చర్చించడం ఈ వ్యాసం ముఖ్యోద్దేశ్యం. ఈ కొలతలకోసం ఉపయోగించిన చాలా పదాలు గ్రామ ప్రాంతాలలో ఇప్పటికీ నిత్యజీవితంలో వాడుతూనే ఉన్నారు. అయితే ఈ పదాలకి పూర్వ కొలమాన పద్ధతిలో నిర్దేశించిన ప్రామాణికార్థం ఈనాటి వాడుకలో నశించిందనే చెప్పాలి. ఈ కొలమానానికి ఉపయోగించిన చిహ్నాలను తెలుగు యూనికోడ్ వర్ణమాలకు అదనపు సంకేతాలుగా చేర్చాల్సిన అవసరం గురించి కొంత ప్రచారం చెయ్యటం కూడా ఈ వ్యాసంయొక్క మరో ఉద్దేశ్యం.
భిన్నాంక చిహ్నాలు
తెలుగు ప్రజలు శాసనకాలం నుండి సంఖ్యలను దశాంశ పద్ధతి (decimal numeral system) లోనే రాసేవారని మనకు తెలుస్తోంది. కానీ భిన్నాలను అంకెల రూపంలో రాయడానికి మాత్రం చతుర్థాంశ పద్ధతి (base-4) పాటించేవారు. ప్రతి భిన్నాంకాన్ని 1/4 ఘాతాల (powers of 1/4) కూడికగా సూచించడానికి ఆయా స్థానాల్లో దానికి సంబంధించిన చిహ్నాన్ని ఉంచేవారు. అంటే ఒక సంఖ్య యొక్క పూర్ణభాగాన్ని(whole number) దశాంశం (decimal)లో రాసి, భిన్న భాగాన్ని (fraction) మాత్రం చతుర్థాంశ (quaternary numeral system) పద్ధతిలో రాసేవారు. ఇది ఎందుకూ పనికిరాని పాత పద్ధతి అని కొట్టేయకండి. నిన్న మొన్నటిదాకా (ఫిబ్రవరి 2001 దాకా) న్యూయార్క్ స్టాక్ ఎక్స్చేంజ్ దాదాపు ఇలాంటి పద్ధతిలోనే స్టాక్మార్కెట్ లావాదేవీలన్నీ నిర్వహించేదని మాత్రం గుర్తుంచుకోండి!
అయితే ఇక్కడ ఒక ఆశ్చర్యం కలిగించే అంశం ఒకటుంది: చతుర్థాంక పద్ధతికి కావల్సింది నాలుగే చిహ్నాలైతే ఎందుకో మన వారు ఎనమిది చిహ్నాలను వినియోగించారు. సరిస్థానంలో వచ్చే భిన్నాంకాలకు ఒక నాలుగు చిహ్నాల సమితి(set) ని వాడితే, బేసి స్థానంలో వచ్చే భిన్నాంకాలకు ఇంకో నాలుగు చిహ్నాలను వాడారు.
| అంకె | బేసి స్థానం | సరి స్థానం |
|---|---|---|
| 0 |  |
 |
| 1 |  |
 |
| 2 |  |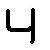
 |
| 3 |  |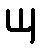
 |
పై పట్టికలో చిహ్నాల వ్యుత్పత్తి సులభంగానే వివరించవచ్చు. బేసి స్థానంలో వచ్చే అంకె ఒకటి అయితే ఒక నిలువు గీత, రెండయితే రెండు నిలువు గీతలు, మూడైతే మూడు నిలువు గీతలు గీసేవారని కనిపెట్టడం అంత కష్టం కాదు. అట్లాగే సరి స్థానంలో అంకె ఒకటి అని చెప్పడానికి ఒక అడ్డంగీత, రెండైతే రెండు అడ్డంగీతలు, మూడైతే మూడు అడ్డం గీతలు గీసేవారని కొంచెం పరిశీలనగా చూస్తే తెలిసిపోతుంది. బేసిస్థానంలో వచ్చే సున్నను హళ్ళి అని పిలిచే వారు. సరిస్థానంలో సున్నను సున్నగానే వ్యవహరించేవారు. “హళ్ళికి హళ్ళి, సున్నకు సున్న” అన్న నానుడికి ఈ కొలతలే ఆధారం.
ప్రతి భిన్నాంకాన్ని దాని స్థానాన్ని బట్టి వేర్వేరు పేర్లతో పిలిచేవారు. ఈ పద్ధతిలో 3/4096 దాకా అన్ని భిన్నాంకాలకి పేర్లుండటం ఆశ్చర్యకరమే! అంటే తెలుగు వారి లెక్కల్లో 3/4096 దాకా భిన్నాలను వాడటం అంత అసాధారణమైన విషయమేమీ కాదన్నమాట. అంతే కాక మొదటి నాలుగు భిన్నాంకాల సమూహాన్ని వదిలేస్తే మిగిలిన ఒక్కొక్క సమూహానికి ఒక్కో అక్షర సూచిక (abbreviation) ను వాడేవారు. ఉదాహరణకు, 
1/4 ని సూచిస్తే, కా 1/64 ని సూచిస్తుంది. అట్లాగే సు 1/1024 ని సూచిస్తుంది. అన్ని భిన్నాంకాల వివరాలు, వాటి అక్షర సూచికలు ఈ క్రింది పట్టికలో చూడవచ్చు.
| పేరు | విలువ | చిహ్నము | అక్షర సూచిక |
|---|---|---|---|
| కాలు | 1/4 |  |
- |
| అర | 1/2 |  |
- |
| ముక్కాలు | 3/4 |  |
- |
| వీసము | 1/16 |  |
వి |
| పరక | 1/8 |  |
వి |
| మువ్వీసము | 3/16 |  |
వి |
| కాని | 1/64 | |
కా |
| అరవీసము | 1/32 | |
కా |
| ముక్కాని | 3/64 | |
కా |
| ప్రియ | 1/256 | |
ప్రి |
| అరకాని | 1/128 | |
ప్రి |
| ముప్ప్రియ | 3/256 | |
ప్రి |
| సుర | 1/1024 | |
సు |
| రెండు సురలు | 1/512 | |
సు |
| మూడు సురలు | 3/1024 | |
సు |
| గోకరకాని | 1/4096 | |
గో |
| రెండు గోకరకానులు | 1/2048 | |
గో |
| మూడు గోకరకానులు | 3/4096 | |
గో |
ఉదాహరణలు:
- 3/8 భిన్నమును ఇలా రాసే వారు ౦
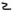(1 * 1/4 + 2 * 1/16) - 5/8 = ౦
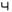
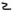(2 * 1/4 + 2 * 1/16) - 7/8 = ౦
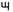
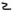(3 * 1/4 + 2 * 1/16) - 5/16 =౦
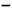(1 * 1/4 + 1 * 1/16) - 7/16 = ౦
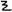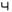
(1 * 1/4 + 3 * 1/16) - 9/16 = ౦ 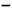(2 * 1/4 + 1 * 1/16)
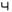
- 11/16 = ౦ 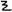(2 * 1/4 + 3 * 1/16)
- 13/16 = ౦
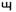
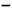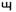
(3 * 1/4 + 1 * 1/16) - 15/16 = ౦ 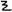(3 * 1/4 + 3 * 1/16)
- π విలువ (దాదాపు 3.14160) ఇలా రాసేవారు ౩
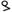
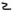
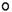
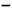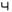
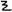
(3 + 0 * 1/4 + 2 * 1/16 + 1 * 1/64 + 0 * 1/256 + 1 * 1/1024) - గణితశాస్త్ర స్థిరాంకం e (దాదాపు 2.718) = ౨ 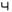(2 + 2 * 1/4 + 3 * 1/16 + 2 * 1/64)
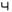
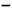
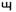
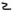
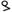
- సువర్ణ నిష్పత్తి (golden ratio) φ (దాదాపు 1.618) = ౧ 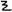(1 + 2 * 1/4 + 1 * 1/16 + 3 * 1/64 + 2 * 1/256 + 0 * 1/1024 + 3 * 1/4096)
కొలమానములు
కొలమానము అన్న పదం దుష్టసమాసమే అయినా కొలతల ప్రమాణికతను సూచించడానికి చాలా కాలంగా పాఠ్యపుస్తకాలలో కూడా వాడుతున్న పదం ఇది. తెలుగువారి కొలమానాలు ముఖ్యంగా మూడు రకాలు: పరిమాణము (volume), ఉన్మానము (weight), ప్రమాణము (length). మొదటిరకం కొలతలు ఘనపరిమాణాన్ని సూచించడానికి వాడితే, రెండవ రకం బరువును సూచించడానికి, మూడవరకం కొలతలు పొడవును, వైశాల్యాన్ని కొలవడానికి వినియోగించేవారు.
18వ శతాబ్దారభం వరకూ ఘనపరిమాణాన్ని ఖచ్చితంగా కొలిచే సాధనాలు లేనందువల్ల, పాత్రల ఘనపరిణామాన్ని అందులో సరిపోయే పదార్థాల బరువు ఆధారంగా నిర్ణయించేవారు[4]. అట్లాగే ప్రామాణిక కొలపాత్రలను పదార్థాల బరువును సూచించడానికి కూడా వాడుకునేవారు. అందుకనే సోల, గిద్ద, మానిక అన్న పరిమాణాలను కొలవడానికి ఒక్కో పదార్థానికి ఒక్కో రకమైన కొలపాత్రను వాడేవారు. వివిధ ధాన్యాలకు వాడే వేర్వేరు కొలపాత్రలు ఇప్పటికీ గ్రామ ప్రాంతాలలో చూడవచ్చు.
పరిమాణము - ఉన్మానము
ఈ విభాగంలో ఘనపరిమాణానికి వాడే “పుట్టి” అనే కొలత గురించి చెప్పి, మిగిలిన పరిమాణాల్ని “పుట్టి” ఆధారంగా వివరింపబడింది. అయితే, పైన చెప్పినట్టుగా ఈ ఘనపరిమాణపు కొలతలన్నిటిని బరువును సూచించే అర్థంలో కూడా తరచుగా వాడుతూ ఉండేవారని గ్రహించాలి.
పుట్టి
పరిమాణాన్ని సూచించే కొలతలో అతి పెద్దది “పుట్టి”. దీనికి “ఖండి” అనే పేరు కూడా ఉండేది. రాసేటప్పుడు ఈ కొలతను సూచించడానికి “ఖ” అనే అక్షరం వాడేవారు. “పుట్టెడు విత్తనాల పట్టెడు నేల” అన్నది సామెత. “పుట్టి” పరిమాణం గల విత్తనాల రాశిని నేలలో నాటితే అవి ఆక్రమించే భూభాగాన్ని సూచిస్తుందీ సామెత. పుట్టిలో ఇరవయ్యో భాగాన్ని “తూము” అని కూడా అంటారు. తూము కొలతకు అక్షర సూచికగా 
ని వాడేవారు. కొన్ని ప్రాంతాలలో దీన్ని “న” అనే అక్షరంతో సూచించే వారు. “పుట్టి” విభజనను ఈ క్రింది పట్టికలో చూడవచ్చు.
| తూము |  ౧ |
| ఇద్దుము | ౨ |
| ముత్తుము | ౩ |
| నల్తుము | ౪ |
| ఏదుము | ఖ౦ ౦ |
| ఆర్దుము | ఖ౦ ౧ |
| ఏడ్దుము | ఖ౦ ౨ |
| ఎనమందుము | ఖ౦ ౩ |
| తొమ్మందుము | ఖ౦ ౪ |
| పందుము | ఖ౦ ౦ |
| పదకొల్తుము | ఖ౦ ౧ |
| పన్నిద్దుము | ఖ౦ ౨ |
| పదముత్తుము | ఖ౦ ౩ |
| పధ్నల్తుము | ఖ౦ ౪ |
| పదిహేదుము | ఖ౦ ౦ |
| పదహార్దుము | ఖ౦ ౧ |
| పదిహేడ్దుము | ఖ౦ ౨ |
| పధెనమందుము | ఖ౦ ౩ |
| పంధొమ్మందుము | ఖ౦ ౪ |
| పుట్టి | ఖ౧ |
ఒక తూము నాలగు కుంచలకు సమానము. తూము కొలతలను ఇలా విభజించవచ్చు:
| కుంచము | |
| ఇరస | |
| ముక్కుస | |
| తూము | ౧ |
ప్రతి కుంచము నాలుగు మానికలకు సమానము.
| మానిక | మా౧ |
| అడ్డ | మా౨ |
| మూడు మానికలు | మా౩ |
| కుంచము | |
నాలుగు సోలలు ఒక మానికకు సమానము.
| సోల | సో౧ |
| తవ్వ | సో౨ |
| మూడు సోలలు | సో౩ |
| మానిక | మా౧ |
ప్రతి సోల నాలుగు గిద్దలకు సమానము.
| గిద్ద | గి౧ |
| అర సోల | గి౨ |
| మూడు గిద్దలు | గి౩ |
| సోల | సో౧ |
బారువ
బరువులను సూచించే కొలతలలో అతి పెద్దది “బారువ”. బారువలో 20 వ వంతు ఒక మణుగు. దానిని “మ” అనే అక్షరంతో సూచించేవారు. ప్రతి మణుగు ఎనమిది వీశెలు (వీ), ప్రతి వీశె అయిదు శేర్లు (శే). మణుగు విభజనలను ఈ క్రింది పట్టికలో చూడవచ్చు.
| ఎత్తు (వి. ఎత్తెడు) |
మ ౦ ౦ |
| అర్ధ మణుగు | మ ౦ ౦ |
| మూడెత్తులు | మ ౦ ౦ |
| వీశె (వి. వీశెడు) |
వీ ౧ or శే ౫ |
| అరవీశె | శే ౨ ౦ |
| సవాశేరు శేరుంపావు |
శే ౧ ౦ |
| అర్ధశేరు నవటాకు | శే ౦ |
| అర్ధశేరు | శే ౦ ౦ |
| పావుశేరు | శే ౦ ౦ |
| నవటాకు | శే ౦ |
| చటాకు | శే ౦ |
“ఏడు మల్లెలెత్తు దానా” అన్న పాటలో “ఎత్తు” బరువును సూచించే పదమని నాకు కొలతల గురించి ఈ మధ్య చదివేంతవరకూ స్ఫురించనేలేదు.
ఇతర కొలతలు
8 మణుగులు ఒక సాగరము. ప్రతి నవటాకు మూడు తులాలకు సమానము. ఒక తులము ఆనాటి పదహారణాల కాసు బరువు కు సమానం.
ప్రమాణపు కొలతలు
పొడవు (length)
పొడవుకు సంబంధించిన కొలతలలో అతి పెద్ద కొలత ఒక యోజనము, దీన్ని కొన్నిచోట్ల ఆమడ అని కూడా వ్యవహరిస్తారు. (బ్రిటిష్ ప్రభుత్వ కాలంలో ఆమడను దాదాపు 10 మైళ్ళుగా ప్రామాణీకరించారు). ప్రతి యోజనము నాలుగు పరుగులు లేదా నాలుగు కోసులు. కోసు లేదా పరుగు ఎంత దూరం అన్న విషయం మాత్రం ప్రాంతాన్ని బట్టి రెండు మైళ్ళ నుండి రెండున్నర మైళ్ళ దాకా మారుతుంటుంది. పరుగు లేదా కోసు 1000 దండములకు సమానము. ప్రతి దండము రెండు బారలైతే, ప్రతి బార రెండు గజాలకు సమానము. ప్రతి గజము రెండు మూరలకు సమానము. అట్లాగే, ప్రతి గజము మూడు అడుగులకు సమానము. ప్రతి అడుగు పన్నెండు అంగుళాలు. ప్రతి మూర రెండు జేనలు. ప్రతి జేన మూడు బెత్తెలు.
వైశాల్యము (area)
వైశాల్యాన్ని కొలవడానికి కుంట లేదా గుంట అనే కొలతను ప్రధానంగా ఉపయోగించే వారు. కానీ, ఇంగ్లీష్ వారి ద్వారా ప్రవేశించిన ఎకరము (Acre) గత రెండు శతాబ్దాల్లో వైశాల్యానికి ప్రాథమిక ప్రమాణంగా మారింది. కుంట అన్న పదం పాత కాలపు బావిని సూచించే పదం. ఒక కుంటలోని నీళ్ళతో ఎంత భాగం నేలను సాగు చెయ్యగలమో ఆ భూభాగాన్ని కుంట అని అనేవారని తెలుస్తోంది. అయితే, ఈ కొలత కూడా ప్రాంతాన్ని బట్టి మారుతూ ఉండేది. ముంబైలో 40 కుంటలు ఒక ఎకరానికి సమానము. కొన్ని చోట్ల చిన్న కుంటలు, పెద్ద కుంటలు అని కుంటలను రెండు రకాలగా వ్యవహరించడం కూడా కనిపిస్తుంది. ఒక గొఱ్ఱు 50 పెద్ద కుంటలకు, 125 చిన్న కుంటలకు సమానము. 64 కుంటలను ఒక కుచ్చెల అనేవారు.
యూనీకోడ్ వర్ణమాల
కంప్యూటర్లు ప్రధానంగా అంకెలతో పని చేస్తాయి. ఒక్కో అక్షరానికీ, వర్ణానికీ ఒక్కో సంఖ్యని కేటాయించి నిక్షిప్తం చేసుకొంటాయి. యూనీకోడ్ కనుగొనక ముందు తెలుగు భాషలోని అక్షరాలకు ఈ విధంగా సంఖ్యలని కేటాయించడంకోసం పరస్పర విరుద్ధమైన సంకేతలిపి (encoding) పద్ధతులను ఎవరికి వారు తయారు చేసుకొని వాడుకోవడం మొదలు పెట్టారు. దీనికి ఒక రకంగా పాత టెక్నాలజీ లోని లోపమే కారణమని చెప్పవచ్చు. యూనీకోడ్ ప్రవేశానికి పూర్వం భాషలలోని అక్షరాలకు సంఖ్యలను కేటాయించడానికి 256 సంకేత స్థలాలు (code points) మాత్రమే ఉండేవి. ఒక్క ఇంగ్లీషు భాషలోని అన్ని అక్షరాలు, సాధారణ వాడుకలో ఉన్న వ్యాకరణ, సాంకేతిక వర్ణాలకే ఈ సంకేత స్థలాలు సరిపోయేవి కాదు.
యూనీకోడ్ టెక్నాలజీతో అక్షరాలకు సంఖ్యలను కేటాయించడం కోసం ప్రాథమిక స్థాయి(Basic Multilingual Plane) లోనే 65536 సంకేత స్థలాలను నియోగించారు. ప్రపంచంలోని అన్ని లిఖిత భాషలకు ప్రత్యేక సంకేత సంఖ్యలను కేటాయించగలిగేంతటి స్థలం ఇది. అందుకే యూనీకోడ్ సంకేతలిపిని విశ్వ వర్ణమాల (Universal Alphabet) అని కూడా పిలుస్తారు. ఈ ఆధునిక కంప్యూటర్ యుగంలో ఆంగ్లేతర భాషల మనుగడకు యూనీకోడ్ ప్రమాణ అవతరణ ఒక వరం అని కూడా చెప్పుకోవచ్చు.
ప్రస్తుతపు యూనీకోడ్ ప్రమాణము (వెర్షన్ 4.1) లో ఆధునిక తెలుగును రాయడానికి కావలసిన సంకేతాలన్నీ ఉన్నాయి. అయితే, ప్రాచీన తెలుగు పుస్తకాలను, తాళపత్రాలను డిజిటల్ రూపంలో గ్రంథస్తం చెయ్యడానికి ఇంకొన్ని సంకేతాలను యూనీకోడ్ వర్ణమాల చేర్చాల్సిన అవసరం ఉంది. ఈ వ్యాసంలో చర్చించిన అంశాల ఆధారంగా 8 సంకేతాలను కొత్తగా జతపర్చాలని నా ప్రతిపాదన. ఇందులో, పట్టిక 1 లో చూపిన 6 సంకేతాలు (1, 2, 3 భిన్నాంకాలకు 2 చిహ్నాల చొప్పున 6 సంకేతాలు), హళ్ళి కి ఒక సంకేతం (సున్నకి వేరే సంకేతం అవసరం లేదు), తూము ను సూచించడానికి మరో సంకేతం. నేను ప్రతిపాదించదల్చుకున్న 8 సంకేతాలను, వాటి సంకేత స్థలాల (Code Points)ను, వాటి పేర్లను ఈ కింది పట్టిక లో చూడవచ్చు.
| 0C78 |  |
TELUGU SIGN HAḶḶI |
| 0C79 | |
TELUGU FRACTION 1/4n, for odd n |
| 0C7A | |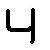
TELUGU FRACTION 2/4n, for odd n |
| 0C7B | |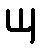
TELUGU FRACTION 3/4n, for odd n |
| 0C7C | |
TELUGU FRACTION 1/4n, for even n |
| 0C7D | |
TELUGU FRACTION 2/4n, for even n |
| 0C7E |  |
TELUGU FRACTION 3/4n, for even n |
| 0C7F |  |
TELUGU SIGN TŪMU |
కృతజ్ఞతలు
ఈ వ్యాసరచలో నాకు సహాయ పడ్డ సురేశ్ కొలిచాల, విజయ సాగర్ విన్నకోట, మైకెల్ ఎవెర్సన్, డా. జెజ్జాల కృష్ణమోహన రావు, పరుచూరి శ్రీనివాస్, డా. రావు వేమూరి, పద్మ ఇంద్రగంటి కి ప్రత్యేక ధన్యవాదాలు. ఈ వ్యాసంలోని కొలమాన పద్ధతుల వివరాలు చాలా వరకు బ్రౌన్[1][3], కాంప్బెల్[2] రాసిన పుస్తకాల నుండి సేకరించినవే. యూనికోడ్ గురించి రాసిన మొదటి రెండు పేరాలకు ఆధారం The Unicode Standard Version 4.0 [5] .
ఆధార గ్రంథాలు
- Charles Philip Brown. 1856 (2006). The Grammar of the Telugu Language, 2nd Edition. Chennai: Asian Educational Society. ISBN 81-206-0041-X.
- A.D. Campbell. 1849 (1991). Grammar of the Teloogoo Language, 3rd Edition. Chennai: Asian Educational Society. ISBN 81-206- 0366-4.
- Charles Philip Brown, Revised by M Veṁkaṭa Ratnaṁ, W H Campbell, Kaṁdukūri Vīrēśaliṁgaṁ. 1903 (2004). Telugu-English Dictionary = Nighaṁṭuvu Telugu - Iṁglīṣh, 2nd Edition. Chennai: Asian Educational Society. ISBN 81-206-0037-1
- Russ Rowlett, “Units: Customary Units”, 23 February 2001, (10 June 2006).
- The Unicode Consortium. 2003. The Unicode Standard, Version 4.0. Addison-Wesley Professional. ISBN 03-211-8578-1
- Unicode, Inc., “Unicode Home Page”, (10 June 2006).
- Pudūri Sītārāmaśāstrulu. 1847 (1916). Peddabālaśiksha. Cennapuri: Vaviḷḷa Rāmaswāmisāstrulu Aṃḍ Sans.
Kiran Kumar Chava అభిప్రాయం:
July 2, 2006 11:10 pm
Great Essay.
Perfect essay/essays for Telugu Wikipedia. Can you also take the pain to put this in Telugu wiki? Probably u can add in section తెలుగుదనం.
Rao Vemuri అభిప్రాయం:
July 3, 2006 8:34 am
నాగార్జున ఇటువంటి వ్యాసాలని ఇంకా రాయాలని కోరుతున్నాను. మన భాష పరిపుష్టం కావాలంటే మన రాతలు ఒక్క కథలకీ, కవితలకీ పరిమితం కాకుండా ఇలా అనేక రంగాలలో అంశాలని తీసుకుని రాయాలి. అప్పుడే పాతబడ్డ మాటలని తిరిగి పలుకుబడిలోకి తీసుకురావచ్చు. కొత్త కొత్త మాటలని పుట్టించనూ వచ్చు.
Rohiniprasad అభిప్రాయం:
July 3, 2006 10:45 am
ఈ వ్యాసంలో విలువైన సమాచారం చాలా ఉంది. మన దేశంలో క్రీ.పూ.6500 ప్రాంతాల నుంచీ వ్యవసాయం మొదలైందని అంటారు. క్రీ.పూ. నాలుగో శతాబ్దంలోనే భూమి విస్తీర్ణతా, పొలాల మీద వచ్చే దిగుబడీ, వాటికి కట్టవలసిన ప్రభుత్వ శిస్తు లెక్కలూ అనీ ఖచ్చితంగా పాటించేవారని తెలుస్తోంది. అందుచేత కొలమానపు పద్ధతులన్నీ ఎప్పటినుంచో అమలులో ఉన్నాయన్న విషయం ఆశ్చర్యకరం కాదు. ఎటొచ్చీ ఇంత వివరంగా వీటి గురించి మనవంటివారికి తెలియజెప్పే వ్యాసాలు అరుదైనవి. రచయితకు ప్రత్యేక అభినందనలు.
విప్లవ్ అభిప్రాయం:
July 7, 2006 10:03 am
ప్రాచీన తెలుగులో కాలాన్ని కొలవడం గురించి కూడా ఉండే ఉంటుంది, రెప్పపాటు, ఘడియలు, ఝాములు, పొద్దులు, మాపులు అని మరికొన్ని పదాలు ఉండి ఉంటయి సమయాన్ని సూచించటానికి. వాటిని కూడా కలిపితే బాగుంటుందేమో?
{ప్రాచీన తెలుగులో “కాలాన్ని బట్టి దూరం మారుతుంది” అని ఎవరూ రాయలేదంటే ఆశ్చర్యమే.}
స్వర్ణకారులు వాడే కొలతలు కనిపించలేదు ఈ వ్యాసంలో, తులం వంటివి (ఎన్ని వీసాలైతే ఒక తులం (పాత తులం)? జవాబు వ్యాసంలో ఉంది, కానీ క్యాలిక్యులేటర్లకు అలవాటు పడ్డ మన బుర్రలు కొద్దిగా వెతకాల్సొస్తుంది.) (గురివింద గింజలతో బంగారం కొలవగా చూసాన్నేను చిన్నప్పుడు, వాటి బరువెంత?).
వైశాల్యం, బొంబాయిలో నే కాదు హైదరాబాదు రాష్ట్రంలో కూడా కుంట లేక గుంట అంటే 120 గజాలే. ఇప్పటికీ 40 గుంటలు ఒక ఎకరమే. “సెంటు” భూమి అంటే ఎంతో కూడా వ్యాసంలో చెప్పవలసింది (సెంటు ప్రాచీనమైనా కాకపోయినా సరే, ఇప్పటి వాడుక కూడా తెలిస్తే అన్వయించుకుని గుర్తుంచుకోవటానికి వీలుంటుంది).
విప్లవ్
Siddineni Bhavanarayana అభిప్రాయం:
March 31, 2012 10:17 pm
నాగార్జున వెన్నగారూ,
As my exposure to computers and to phonetics is drastically limited, I am unaware if some phonemes, endemic to Telugu language have been assigned with special characters in unicode. Voiceless palato-alveolar affricate, which has three variants with phonemic distinction between one and the rest of the consonantal sounds, is fast losing its distinction between its variants, save the distinction caused by aspiration. Could you please clarify if the unaspirated variant of the consonant can be written in Unicode (I have not come across any such instance where the consonant was written with a special mark)?
“ప్రతి వీశె అయిదు శేర్లు” It might not have been standardized in all regions. I remember having read that a ‘veese’ was equal to four ’serus’.
I sincerely request you to explore further and give us more, esp. as to the variations in indigenous terminology and the loan jargon from Sanskrit, Persian and English and regarding various stages in standardization from Raja Todar Mall to Thomas Munroe!
Kindly accept my earnest thanks for giving us very valuable information.
Siddineni Bhavanarayana
Siddineni Bhava Narayana అభిప్రాయం:
April 8, 2012 12:05 am
Nagarjuna Garu,
Archival revenue records such as Siddhavatam kaifeeyat is said to contain many reverences to types of land and measuring units of land, purportedly for laying down the rate of cess in pecuniary units. I wish some one had researched the monetary area. A lot of research is yet to be done on the linguistic aspect of the terminology and on the social conditions in which the units were in usage.
Units like ‘mandya’ and ‘ankanam’ are referred to in Telugu and Kannada areas. Copper plate inscription NO: 1, collected in “Copper - Plate and Stone Inscriptions of South India “, By Alan Butterworth And V. Chetty Venugopal cites the inscription named “ Parachur Grant “ of Devaraya given to be of S S 1 312. corresponding to 1309 A D.
The Sanskrit text in Telugu script is crammed with Telugu names and terminology. It mentions he grant , to one Chennu Bhatta of Bharadwaja Gotra ,of a village measuring fifteen mandyas in extent, lying on either side of the river named Audala near Parachur[ with a consonantal ending] in Addanki Seema. These units of measurement for area of arable land is left undefined. Could these units of measure be explained?
Yours faithfully,
Siddineni Bhava Narayana