n అడ్డ వరుసలు, n+1 నిడుద వరుసల చుక్కలతో నిర్మించిన ఒకే గీతతో ఉండే సోనా ముగ్గులను నాలుగు వైపులలో పొడిగించగా ఏర్పడిన ఒకే గీత గల ముగ్గులు నిడుద సోనా ముగ్గులు (నిసోములు). ఇవి 222 సౌష్ఠవ వర్గమునకు చెందిన ముగ్గులు. వీటిలోని చుక్కల సంఖ్య 2.n2. n సంఖ్యగల నిసోము n-1, n-2, … ఇత్యాదుల నిసోములను తనలో ఇముడ్చుకొని ఉంటుంది. నాలుగు n నిసోములతో ఒక 2n నిసోమును సృష్టించవచ్చును. ఈ నిసోముల అమరిక పరమాణువులోని కక్ష్యలలో, ఉపకక్ష్యలలో సంచరించే గరిష్ఠ ఎలక్ట్రానుల సంఖ్యకు ఒక నమూనాగా తలచవచ్చును.
పరిచయము
ముగ్గులను రెండు విధములుగా వేయవచ్చును. అవి చుక్కలు లేనివి, చుక్కలతో నున్నవి. చుక్కలు లేకుండ ఒక నమూనాను స్వతంత్రముగా కల్పించి రంగులతో నింపి నేలపైననో, గోడపైననో లేక కాగితముపైననో వేయవచ్చును. కొన్ని సమయములలో వీటికి సామ్యరూపము లేక సౌష్ఠవము కూడ ఉంటుంది. ఇట్టి చిత్రములను రంగవల్లులనుట కూడ వాడుక. చుక్కలతో రెండు విధములైన ముగ్గులను గీయవచ్చును. చుక్కలను మార్గదర్శిగా నుంచుకొని సౌష్ఠవభరిత చిత్రములను గీయవచ్చును. ఇందులోని చుక్కలు కేవలము సహాయకారి మాత్రమే, వీటిని లేకుండ కూడ ఉత్తమ కళాకారిణులు ఇటువంటి ముగ్గులను వేయగలరు. చుక్కలను తాకకుండ వాటి చుట్టు ముగ్గుపొడితో, తడి పిండితో చిత్రవిచిత్రములైన ఆకారములను సృష్టించుటకు వీలవుతుంది. వీటిని మెలిక ముగ్గులు లేక మువ్వల ముగ్గులు అంటారు. తమిళములో వీటిని చిక్కు కోలం అంటారు. వీటిని జాగ్రత్తగా వేసినప్పుడు ఇందులో ముడులు కనబడుతాయి. ఇవి త్రాటితో లేక త్రాళ్ళతో నేసిన తివాచీలలా కూడ ఉంటాయి. ఇవియే నిజమైన మెలిక ముగ్గులు. ప్రపంచములో పరస్పర సంపర్కములు సంబంధములు లేని వివిధ ప్రాంతములలో మనకు ఇట్టి చిత్రములు గోచరమవుతాయి. దీనిని ప్రపంచ సాంస్కృతిక నిక్షేపము అని చెప్పవచ్చును.
దక్షిణ భారతదేశములో ప్రతి దినము పూజాగృహములలో, ఇంటి వాకిలి ముందు వేసే ముడి ముగ్గులు, ఐరోపా ఖండములో కనబడే కెల్టిక్ ముడులు (Celtic knots), ఆఫ్రికా ఖండములో కాంగోలో కనబడే సోనా అమరికలు (Sona patterns) నిజముగా సర్వమానవ సముదాయమునకు చెందిన కళాసంపదయే. ముగ్గులలోని సామ్యరూప సిద్ధాంతములను, ముగ్గుల నిర్మాణములో కనబడే కొన్ని గణితశాస్త్ర రీతులను, సామ్యరూప సౌందర్యమును నేను ఇంతకు ముందు కొన్ని వ్యాసములలో (కౌముది, ఈమాట1, ఈమాట2) చర్చించియున్నాను. ప్రస్తుత వ్యాసములో చర్చనీయాంశము 2.n2 చుక్కలతో నేర్పరచిన ఒక ప్రత్యేకమైన ముగ్గుల అమరిక వెనుక గల గణితశాస్త్ర సిద్ధాంతములు.
నిడుద సోనా ముగ్గులు
సోనా ముగ్గులను గురించి ఇంతకు ముందే పరిచయము చేయడము జరిగినది. ఇందులోని చుక్కలలో అడ్డ వరుస (row), నిలువు వరుస (column) సంఖ్యలు సాపేక్షముగా అభాజ్యమయితే (relatively prime) మనకు ఏకరేఖాచిత్రము లభిస్తుంది. ఈ వ్యాసములోని ముగ్గులు n అడ్డ వరుసల, n+1 నిలువు వరుసల చుక్కలుండే ఒంటిగీత ముగ్గులపైన ఆధారపడినవి. n, n+1 ఎప్పుడు సాపేక్ష్యముగా అవిభాజ్యమే, అంటే n=1 అయినప్పుడు తప్ప, మిగిలిన n విలువలకు n+1 సంఖ్యను nతో భాగహారము చేయగా మనకు పూర్ణాంకము (integer) లభించదు. n=10, n+1=11 విలువలతో గీచిన సోనాచిత్రమును ఇంతకు ముందే చూసి యున్నారు.
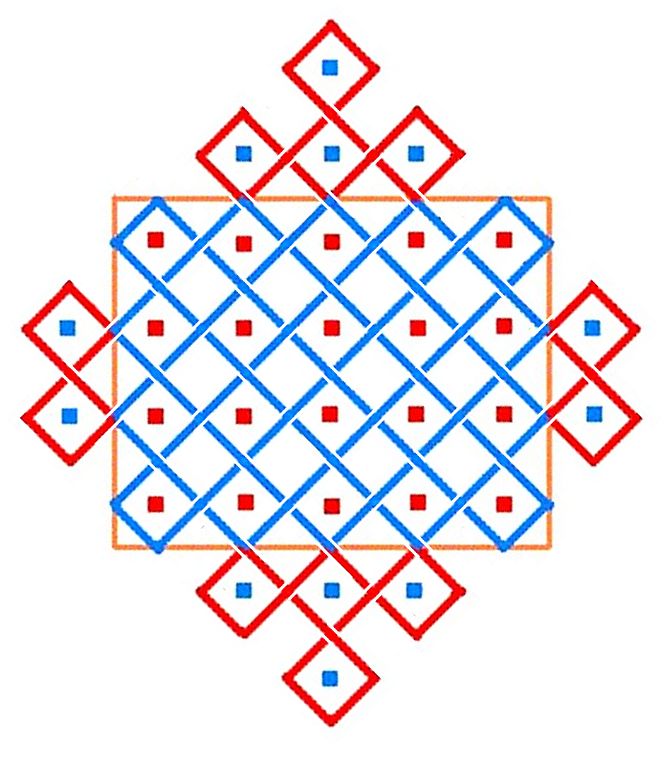
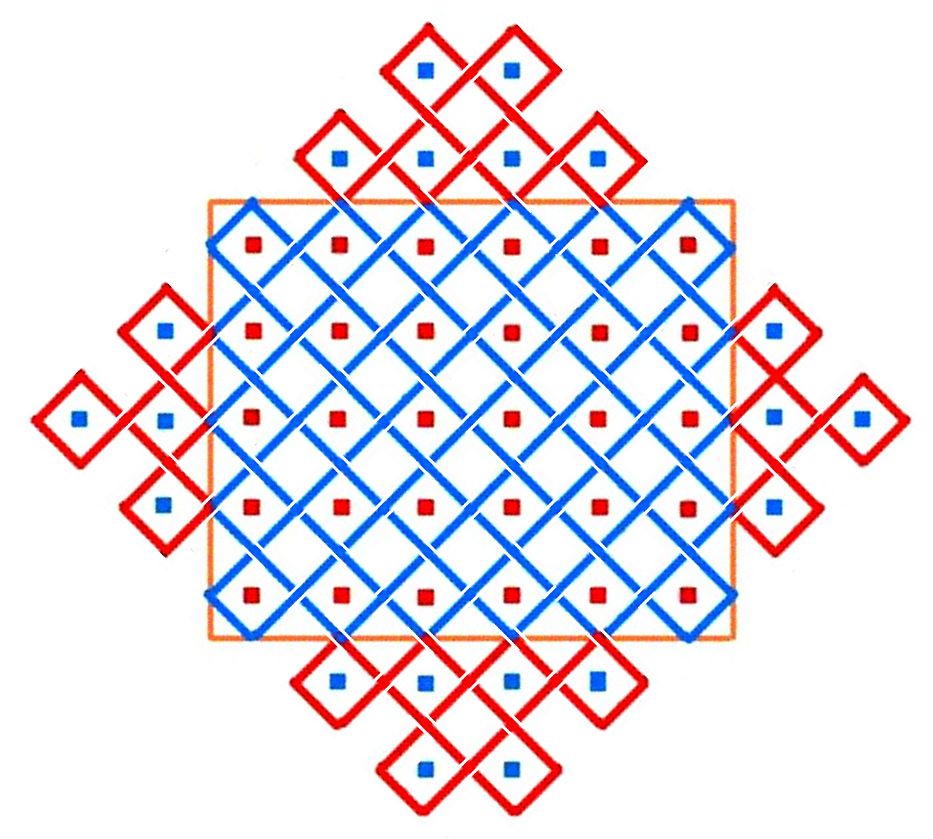
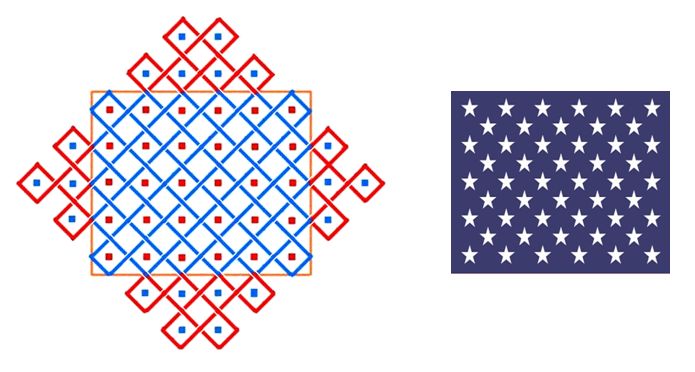
చిత్రము 1a, 1b లను పరిశీలించండి. 1a లోని నారింజరంగు దీర్ఘచతురస్రములో 4 అడ్డ వరుసలు, 5 నిలువు వరుసలు ఉన్నాయి, అదే విధముగా 1b లోని నారింజరంగు దీర్ఘచతురస్రములో 5 అడ్డ వరుసలు, 6 నిలువు వరుసలు ఉన్నాయి. ఎఱ్ఱని రంగుతో చూపబడిన ఈ చుక్కలను కేంద్రీకృతము చేసిన ఏకరేఖాచిత్రము ఊదారంగులో చూపబడినది. ఈ చుక్కల అమరికను పొడిగించుదామా? పైన, క్రింద, ఎడమ, కుడి వైపులలో వీటిని 1a, 1b చిత్రములలో చూపిన తీరులో ఊదా రంగు చుక్కలతో పొడిగించడమైనది. ఈ అన్ని చుక్కలను కేంద్రీకృతము చేసి గీయగా వచ్చిన చిత్రములను ఊదా, ఎఱ్ఱ రంగు గీతలతో చూడవచ్చును. ఇవి కూడ ఏకరేఖాచిత్రములే. చుక్కల సంఖ్యను ఒక వంక పెట్టితే ఈ రెండు చిత్రాల మధ్యనుండే ఒక వ్యత్యాస మేమనగా, వీటి అమరికల రూపము 90 డిగ్రీల మార్పుతో నున్నది. దీనికి కారణము, 1a లో గల సరి, బేసి చుక్కల అమరిక 1b లో 90 డిగ్రీలతో త్రిప్పబడినది. అన్ని చిత్రాలను 1b చిత్రములా ఇక మీద చర్చించే చిత్రములలో అమర్చబడినది. పొడిగింపబడిన ఇట్టి సోనా ముగ్గులను నిడుద సోనా ముగ్గులని (నిసోములు) పిలువ దలచాను.
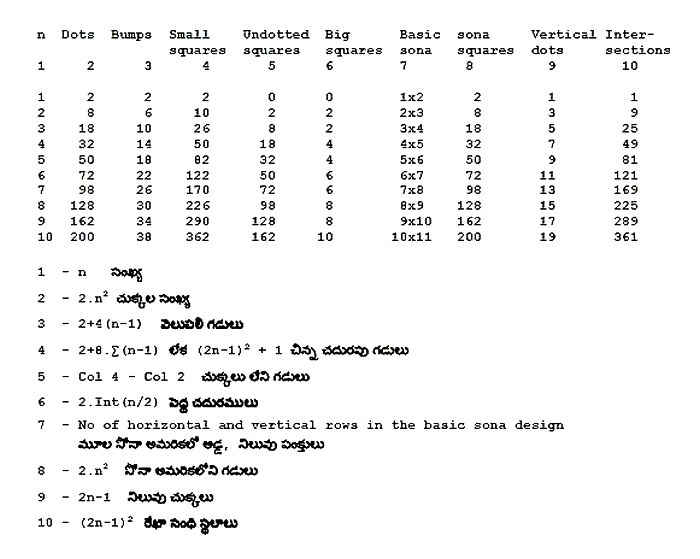
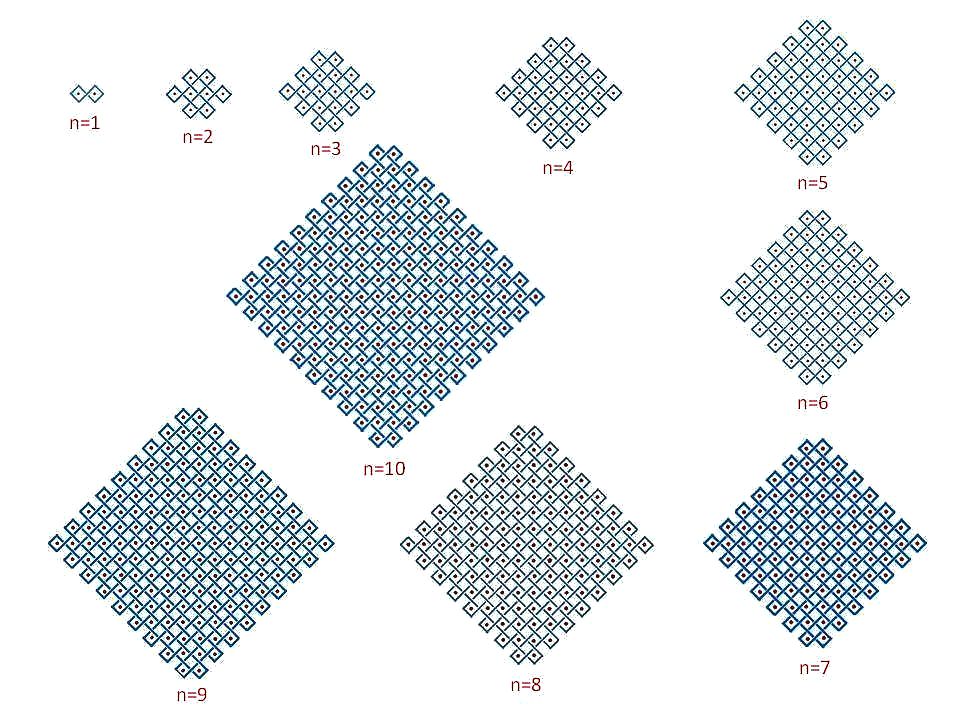
రెండవ చిత్రములో n = 1 నుండి n = 10 వరకు, అనగా 1×2 చుక్కల అమరిక నుండి 10×11 చుక్కల అమరిక వరకు సోనా అమరికలను పొడిగించగా మనకు లభించిన నిసోముల ఏకరేఖాచిత్రములను చూడవచ్చును. ఇంచుమించు అన్ని గడుల పరిమాణము ఒక్కటే. ఈ నిసోము ముగ్గుల కన్నిటికీ ఉండే సౌష్ఠవము 222, అనగా ఒకదానికొకటి లంబాకారముగా ఉండే మూడు ద్విరావృత్త అక్షములు (three mutually perpendicular two-fold axes) ఈ చిత్రములలో కనబడుతాయి. ఇట్టి ముగ్గుల ప్రత్యేక లక్షణములు మొదటి పట్టికలో ఇవ్వబడినవి. వీటి పరిశీలన ద్వార సేకరించిన విషయములను క్రింద చర్చిస్తున్నాను –
నిసోముల గురించి చర్చ
-
ప్రతి నిసోములోని చుక్కల సంఖ్య 2.n2. n = 1 అయినప్పుడు, మనకు 2 చుక్కలుండగా, n = 10 అయినప్పుడు 200 చుక్కలు అవుతుంది. n = 10 అయినప్పుడు లభించిన 200 చుక్కల ముగ్గును మూడవ చిత్రములో చూడవచ్చును. ఇందులో ఎడమవైపు నేను కంప్యూటరుపైన గీచిన చిత్రము, కుడివైపు అదే ముగ్గును నేలపై చుక్కలు పెట్టి శ్రీమతి రాణి శెల్వరాజ్ వేసిన ముగ్గు ఉన్నాయి.
-
ప్రతి నిసోము ఒక సోనా ముగ్గును పొడిగించగా దొరికిన ముగ్గు. ఈ మూల సోనా ముగ్గులో n(n+1) చుక్కలు, n(n-1) చుక్కలు లేని గడులు ఉన్నాయి. ఈ మూల సోనా ముగ్గులో చుక్కలు లేని, చుక్కలున్న మొత్త గడుల సంఖ్య 2.n2. ఇది మనము సృష్టించిన నిసోములోని చుక్కల సంఖ్యయే. ఇందులో మరో ముఖ్యమైన విషయము ఏమంటే, ఈ ఆధార సోనా ముగ్గుల అన్ని గడులలో చుక్కల నుంచితే వచ్చిన అమరికలలో ఒకటి అమెరికా దేశములోని పతాకము నందలి నక్షత్రములలా ఉంటుంది. దీనిని నాలుగవ చిత్రములో గమనించవచ్చును. నారింజరంగులో ఊదా గీతలతో ఉండే 5×6 సోనా ముగ్గులోని అన్ని గడుల అమరిక, కుడివైపు ఉండే అమెరికా సంయుక్త రాష్ట్రముల నక్షత్రముల అమరికతో సరిపోతుంది.
-
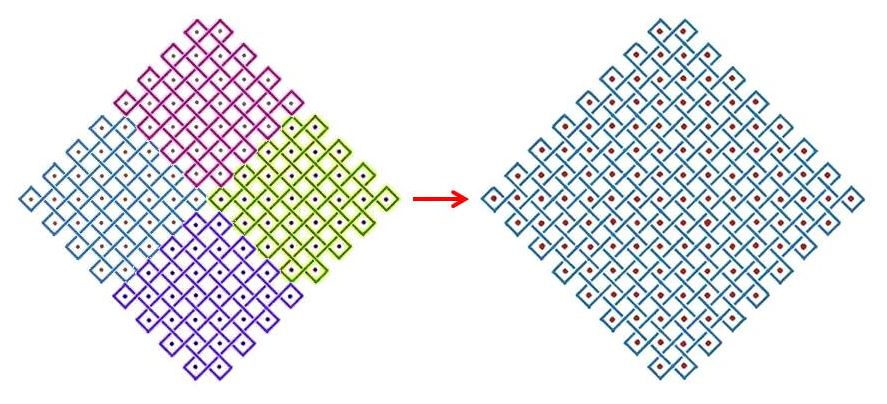
ప్రతియొక్క n విలువ గల నాలుగు నిసోములతో 2n విలువ గలిగిన నిసోమును నిర్మించ వీలగును. ఇది ఐదవ చిత్రములో విశదీకరించబడినది. ఇందులో నాలుగు n=4 నిసోములను చేర్చినప్పుడు ఒక n=8 నిసోము ఏర్పడే విధానము తెలుపబడినది.
-
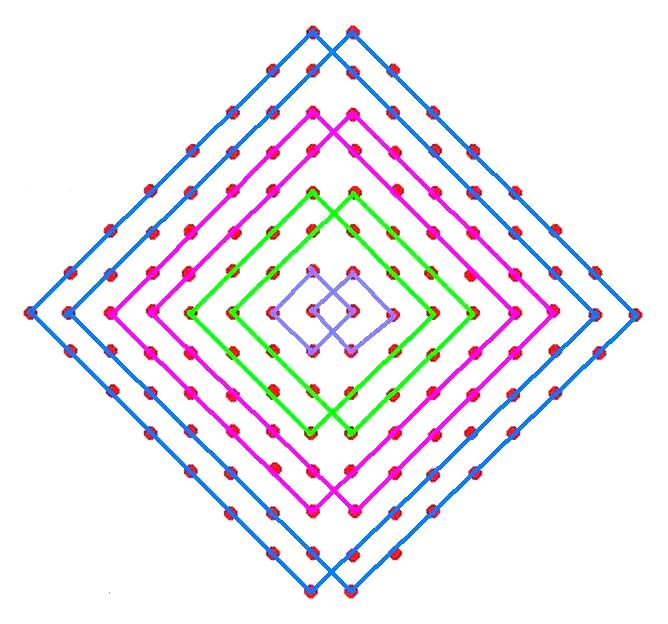
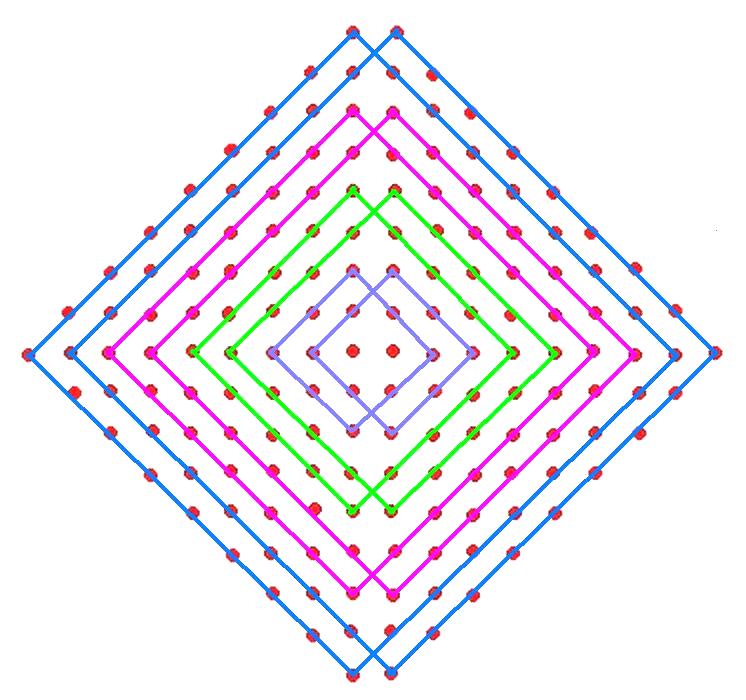
ప్రతి n నిసోముకు చుక్కలుండే వెలుపలి గడుల సంఖ్యను దాని చుక్కల సంఖ్యనుండి (2.n2) తీసివేయగా వచ్చిన సంఖ్య (n-1) నిసోములోని చుక్కల సంఖ్యతో, అనగా 2.(n-1)2 తో సరిపోతుంది. దీని అర్థమేమంటే, n నిసోములో (n-1) నిసోము అంతర్గతమై యున్నది. ఉదాహరణకు, ఆఱవ చిత్రమును చూడండి – ఇది ఒక 5×6 సోనా ముగ్గు ఆధారముగా నిర్మించబడిన n=5 నిసోము. ఇందులోని చుక్కలు 50, వెలుపలి గడులు 18. చుక్కల సంఖ్యనుండి వెలుపలి గడుల సంఖ్య తీసివేయగా మనకు 32 లభిస్తుంది. n=4 నిసోములోని చుక్కల సంఖ్య 32. ఈ చిత్రములో వంగపండు రంగులోని గడులను తొలగిస్తే వచ్చే చిత్రము n=4 నిసోము. ఈ n=4 నిసోముకు వెలుపలి గడుల సంఖ్య 14, ఇవి చిత్రములో చిలుక పచ్చు రంగులో చూపబడినవి. అనగా ఈ నిసోములు రష్యాలోని మాతృష్కా (Matryoshka Doll) బొమ్మలా ఒక దానిలో మరొకటి ఇమిడి ఉంటుందన్నది ఒక ఆసక్తికరమైన విషయమే.
-
చిత్రము 7a. నిసోములలో చతురస్రములునిసోములలో ఉండే చుక్కలను మాత్రము కలిపితే మనకు పెద్ద చతురస్రములు లభిస్తాయి. అవి ఎప్పుడు సరి సంఖ్యలే. పక్కపక్కన ఉండే n సంఖ్యల నిసోములకు ఈ పెద్ద చతురస్రముల సంఖ్య ఒక్కటే. ఉదాహరణకు, n=8, n=9 నిసోములకు 8 పెద్ద చతురస్రములు ఉంటాయి. వీటిని 7a, 7b చిత్రములలో చూడవచ్చును.
- నిసోములోని చుక్కల సంఖ్యయైన 2.n2 సంఖ్య అణుశాస్త్రములో కనబడుతుంది. ఒక పరమాణువునకు (atom) కేంద్రములో (nucleus) న్యూట్రానులు (neutrons), ప్రోటానులు (protons) ఉంటాయి. దానికి బయట కక్ష్యలలో (orbits) ఎలక్ట్రానులు (electrons)తిరుగుతూ ఉంటాయి. ఈ కక్ష్యలను లేక ఎలక్ట్రానుల పరిధులను n = 1, 2, 3, … (Principal quantum numbers) సంఖ్యలతో తెలుపుతారు.
చిత్రము 7b. నిసోములలో చతురస్రములుఒక్కొక్క కక్ష్యలో ఉండే ఎలక్ట్రానుల సంఖ్య 2.n2. అంతే కాక ఈ కక్ష్యలలో ఉపకక్ష్యలు (orbitals)కూడ ఉన్నాయి. ఒక కక్ష్యలో ఉండే ఎలక్ట్రానులు విడివిడిగా ఈ ఉపకక్ష్యలలో సంచారము చేస్తాయి. ఇది సూక్ష్మముగా ఒక పరమాణువు నిర్మాణము. ఈ ఉపకక్ష్యలను s, p, d, f, g … అంటారు. ఈ s, p, d, f, g ఉపకక్ష్యలలోని ఎలక్ట్రానుల గరిష్ఠ సంఖ్య 2, 6, 10, 14, 18, …
ఒక నిసోములో మరొక నిసోము ఇమిడి ఉండే తీరును పైన మీకు తెలిపినాను. ఆఱవ చిత్రమును మళ్ళీ మరొక మారు పరిశీలిద్దామా? ఇందులో n=1 నిసోము నారింజరంగులో చూపబడినది. ఇందులో 2 చుక్కల గడులు ఉన్నాయి. n=2 నిసోముకు ఉన్న 8 చుక్కల గడులు 2 నారింజ, 6 లేత ఊదా రంగు గడులు. 2 నారింజ రంగు గడులను అగ్రములలో తాకే చతురస్రపు గడులు 6 మాత్రమే. ఈ 6 లేత ఊదా రంగు గడులను అగ్రములలో 10 గులాబి రంగు గడులు తాకుతాయి. 2 నారింజ, 6 ఊదా, 10 గులాబి రంగుల గడులను కలిపితే మనకు n=3 నిసోము లభిస్తుంది. ఈ 10 గులాబి రంగుల గడులను అగ్రములలో 14 చిలుక పచ్చ రంగు గడులు మాత్రమే తాక గలవు. 2 నారింజ, 6 ఊదా, 10 గులాబి, 14 పచ్చ రంగు గడులను కలిపితే n=4 నిసోము లభిస్తుంది. 2, 6, 10, 14 మున్నగు సంఖ్యలు s, p, d, f, ఉపకక్ష్యలలో ఉండే గరిష్ఠ ఎలక్ట్రానుల సంఖ్య. 2, 8, 18, 32, మున్నగునవి కక్ష్యలలో ఉండే ఎలక్త్రానుల గరిష్ఠ సంఖ్య. ఈ విధముగా కక్ష్యలలో, ఉపకక్ష్యలలో ఉండగలిగిన ఎలక్ట్రానుల గరిష్ఠ సంఖ్యను ఈ నిసోముల ద్వార మనము గ్రహించుకొనవచ్చును.
ఉపసంహారము
మన ఇండ్లలో అంతగా చదువు రాని వారు, గణితశాస్త్రములో ఏ మాత్రము పరిచయము లేని వారు ఈ వ్యాసములో చర్చించబడిన నిసోము ముగ్గులను చక్కగా వేస్తారు. ఇలాటి మెలిక ముగ్గుల వెనుక గణితశాస్త్ర సిద్ధాంతములు ఎన్నో ఉన్నాయి. వాటిని అందరికీ తెలిసే విధముగా వెలిబుచ్చడమే ఈ వ్యాసపు ముఖ్యోద్దేశము. (ఈ వ్యాసములో ఉపయోగించిన ఒక ముగ్గును వాడుకొనుటకు అనుమతి నిచ్చిన చెన్నైకు చెందిన శ్రీమతి రాణి శెల్వరాజ్ గారికి నా కృతజ్ఞతలు.)