న్యూయార్క్ నగరానికి యాభై మైళ్ళ దూరంలో ఉన్న ప్రిన్స్‌టన్ పట్టణంలో ఎనిమిది వందల ఎకరాల స్థలంలో చెట్లూ, చేమల మధ్య భవంతులతో ఇన్స్టిట్యూట్ ఆఫ్ అడ్వాన్స్డ్ స్టడీ (IAS) అన్న ఓ ప్రపంచ ప్రసిద్ధి గాంచిన పరిశోధనా సంస్థ ఉంది. హిట్లర్ ‘పుణ్యమా’ అని యూరప్ నుండి పారిపోయిన మహామేధావులెందరికో ఆ సంస్థ ఆశ్రయం ఇచ్చింది. 1940-1950 మధ్యలో ఆ సంస్థని చూడటానికి వచ్చే వాళ్ళకి సాయంత్రం ఆఫీసు నుండి ఇంటికి నడచిపోతూ ఇద్దరు వ్యక్తులు కనపడేవారు.

కర్ట్ గూడెల్
1906 – 1978

ఒకాయన లావుగా, పొడవుగా, నలిగిన బట్టలు వేసుకుని చిలిపి కళ్ళతో నవ్వుతూ, తుళ్ళుతూ ఉండేవాడు. ఆయన పక్కనే ఒక బక్క పలచనయిన మనిషి, నలగని బట్టలూ, టోపీ పెట్టుకుని ముభావంగా ఉండేవాడు. ఇన్యూయార్క్ నగరానికి యాభై మైళ్ళ దూరంలో ఉన్న ప్రిన్స్టన్ పట్టణంలో ఎనిమిది వందల ఎకరాల స్థలంలో చెట్లూ, చేమల మధ్య భవంతులతో ఇన్స్టిట్యూట్ ఆఫ్ అడ్వాన్స్డ్ స్టడీ (IAS) అన్న ఓ ప్రపంచ ప్రసిద్ధి గాంచిన పరిశోధనా సంస్థ ఉంది. హిట్లర్ ‘పుణ్యమా’ అని యూరప్ నుండి పారిపోయిన మహామేధావులెందరికో ఆ సంస్థ ఆశ్రయం ఇచ్చింది. 1940-1950 మధ్యలో ఆ సంస్థని చూడటానికి వచ్చే వాళ్ళకి సాయంత్రం ఆఫీసు నుండి ఇంటికి నడచిపోతూ ఇద్దరు వ్యక్తులు కనపడేవారు.

కర్ట్ గూడెల్
1906 – 1978

ఒకాయన లావుగా, పొడవుగా, నలిగిన బట్టలు వేసుకుని చిలిపి కళ్ళతో నవ్వుతూ, తుళ్ళుతూ ఉండేవాడు. ఆయన పక్కనే ఒక బక్క పలచనయిన మనిషి, నలగని బట్టలూ, టోపీ పెట్టుకుని ముభావంగా ఉండేవాడు. ఇద్దరూ గత శతాబ్దంలో విజ్ఞాన శాస్త్రంలో పాతుకుపోయి ఉన్న నమ్మకాలను పెకలించినవారే. కానీ, ఒకరి గురించి సామాన్య ప్రపంచంలో తెలియని వారుండరు. వేరొకరి పేరు విన్నవాళ్ళు అరుదు. ఒకరు ప్రపంచ ప్రఖ్యాతి పొందిన భౌతిక శాస్త్రవేత్త ఆల్బర్ట్ ఐన్‌స్టయిన్, వేరొకరు కర్ట్ గూడెల్.

1979లో ప్రతిష్ఠాకరమైన Pulitzer బహుమతి నందుకున్న ఓ పుస్తకం – డగ్లస్ హాఫ్‌స్టాడర్ రాసిన గూడెల్, ఎషర్, బాక్: ఆన్ ఎటర్నల్ గోల్డెన్ బ్రెయిడ్ – ప్రచురితమైనదాకా గూడెల్ విప్లవాత్మకమైన సిద్ధాంత పరిశోధనల గురించీ ఆయన జీవితం గురించీ సామాన్యులకి తెలిసింది చాలా తక్కువ.

సంపన్న వంశంలో జననం

కర్ట్ ఫ్రీడ్రిష్ గూడెల్ (Kurt Friedrich Gödel) 1906 ఏప్రిల్ 28న అప్పట్లో ఆస్ట్రో-హంగేరియన్ సామ్రాజ్యంలో, బర్నో (Brno) పట్టణంలో పుట్టాడు. మొదటి ప్రపంచ యుద్ధం తర్వాత ఆ సామ్రాజ్యం కూలిపోయింది. బర్నో చెకొస్లోవేకియా అన్న కొత్త దేశంలో భాగమమయింది. గూడెల్ పూర్వీకులు పొట్టపోషణకై జర్మనీ నుండి వలస వచ్చినవారు. బర్నోలో గూడెల్ కుటుంబమే కాకుండా జర్మన్ మాట్లాడే కుటుంబాలు కొంచెం ఎక్కువగానే వుండేవి. కర్ట్ తండ్రి బట్టల కంపెనీలో మేనేజరు. పనివాళ్ళూ సౌకర్యాలతో గూడెల్ కుటుంబం చుట్టుపక్కల వాళ్ళతో పోలిస్తే ఐశ్వర్యవంతులే.

గూడెల్‌కి చిన్నప్పటి నుండీ కుతూహలం ఎక్కువ. నాలుగేళ్ళప్పుడే, ఇంట్లో అతనిని ‘హెర్ వరుమ్’ (Mr. Why) అని పిలిచేవాళ్ళు. పసి వయసులో వాతరోగం పాలయ్యాడు. దాని వలన శారీరకంగా నష్టం కలగకపోయినా, జీవితాంతమూ తనకి వంట్లో బాగులేదనే మానసిక రుగ్మతకు లోనయ్యాడు. ఇది అతని జీవితంలో చివరకి ప్రాణాంతక పరిస్థితులకి దారితీసింది. బడిలో ప్రతి సంవత్సరం అన్ని సబ్జక్టులలో మంచి మార్కులతో ఉత్తీర్ణుడయే వాడు. పధ్నాలుగేళ్ళ వయసులో వినోద యాత్రకని వేరే ఊరు వెళ్ళినప్పుడు, గర్ట(Goethe) జీవిత చరిత్ర చదివాడు. రంగుల సిద్ధాంతం గురించి గోయ్థ న్యూటన్తో పడిన సంఘర్షణ గురించి చదివిన తర్వాత, అతనికి గణితం పైనా సైన్సు పైనా మక్కువ పెరిగింది. 1924లో యూనివర్సిటీ చదువుకి వియన్నా నగరానికి వెళ్ళాడు. అప్పటికే అన్న రుడోల్ఫ్ అక్కడ మెడిసిన్ చదవడానికి వెళ్ళి ఉన్నాడు.

చదువుకునే రోజుల్లోనే గూడెల్ ఓ డాన్సర్‌ని కలిశాడు. ఆమె పేరు అడేల్(Adele). కర్ట్ కన్నా ఆరేళ్ళు పెద్దది; అప్పటికే పెళ్ళయి విడాకులు కూడా పుచ్చుకున్నది; బార్లలో, కాఫీ హౌస్‌లలో పనిచేసేది. అట్లాంటి డాన్సర్లని, శీలం తక్కువ అని సంఘంలో పై వర్గాల వాళ్ళు చిన్నచూపుతో చూసేవాళ్ళు. అందుకని తమ ప్రణయ జీవితం గురింఛి గూడెల్ సన్నిహితులకి కూడా చెప్పలేదు. కలిసిన పదేళ్ళ దాకా పెళ్ళి ప్రస్తావన తేలేదు. కర్ట్ కుటుంబం అసలే సంపన్న సాంప్రదాయక కుటుంబం; వాళ్ళిద్దరి కలయికకి కర్ట్ కుటుంబం సుతరామూ ఒప్పుకోలేదు. అయినా గోడెల్ ఆవిడనే పెళ్ళి చేసుకున్నాడు.

వియెన్నాలో పై చదువు

వియన్నా అపట్లో యూరపులో పేరున్న సాంస్కృతిక కేంద్రం. కాఫీ హౌసుల్లో కూర్చుని గంటల తరబడి చర్చించుకోవడం సర్వ సాధారణం. కొందరు మేధావులు ఓ పాత కాఫీ హౌసులో వారానికోసారి కలిసి తాత్విక విషయాలు చర్చించుకునేవాళ్ళు. వీటికి తన ప్రొఫెసరు ఆహ్వానం పైన గూడెల్ అప్పుడప్పుడు హాజరయేవాడు; కాని మితంగా మాట్లాడేవాడు. ఆ ముఠాకే వియెన్నా బృందం (Vienna Circle) అని పేరు వచ్చింది.

గూడెల్‌కి 1930లో పీహెచ్.డీ పట్టా వచ్చింది. తన థీసిస్లో ప్రతిపాదనా తర్కం (Propositional Logic) సంపూర్ణం (complete) అనీ, వైరుధ్య రహితమనీ (consistent) రుజువు చేశాడు. ఈ పదాల గురించి క్లుప్తంగా తెలుసుకుందాం. మౌలికమైన వివేచనా సూత్రాలను క్రమబద్ధం చేసే తార్కిక వ్యవస్థని ప్రతిపాదనా తర్కం అంటారు. ఓ వ్యవస్థ (system)లో, ఏ ప్రతిఫాదన ఇచ్చినా అది నిజమో కాదో తేల్చి చెప్పగలిగితే ఆ వ్యవస్థ సంపూర్ణం; దాంట్లో వైరుధ్యాలకి ఆస్కారం లేదని రుజువు చేస్తే అది వైరుధ్య రహితం. ప్రతిపాదనా తర్కంలో మనమడిగే ప్రతి ప్రశ్నకీ – ఓ ప్రతిపాదన నిజమా కాదా అన్న ప్రశ్నకి – ఖచ్చితమైన జవాబు దొరుకుతుంది. అంతేకాదు, ఆ తర్కంలో చేసే వివేచన ఎలాంటి వైరుధ్యాలకీ దారి తీయదు.

డాక్టరేట్ డిగ్రీ ఉన్నంత మాత్రాన మంచి జీతంతో యూనివర్సిటీలో లెక్చరరు ఉద్యోగం వచ్చే అవకాశాలు లేవు. అందుకు మరో పేపరు ప్రచురించాలి. దేని మీద రాయాలి? ఎక్కువమందిని ఆకర్షించాలంటే పేరున్న సమస్యనేదైనా తీసుకోవాలి. నూతన శతాబ్దార్భావం సందర్భంగా 1900లో హిల్బర్ట్ గణిత ప్రపంచానికి సాధించమని ఓ సమస్యల చిట్టా ఇచ్చి వున్నాడు. గూడెల్ ఆ లిస్టులో గణిత పునాదులకి సంబంధించిన రెండో సమస్యను తీసుకొన్నాడు. ప్రతిపాదనా తర్కం లాగే, సంఖ్యాశాస్త్రం కూడా సంపూర్ణమనీ, వైరుధ్యరహితమనీ రుజువు చెయ్యడం ఆ సమస్య ధ్యేయం.

సంఖ్యాశాస్త్రం సంపూర్ణమంటే అర్థం ఏమిటి? సంఖ్యలకి సంబంధించిన ఏ ప్రశ్నకయినా సమాధానం చెప్పగలగాలి. చిన్న తరగతులలోనే ప్రధాన సంఖ్యల గురించి చదువుకుంటాం. ప్రధాన సంఖ్యని, అదీ, ఒకటీ తప్ప మరే సంఖ్యా నిశ్శేషంగా విభజించలేదు. 2, 3, 5, 7, 11, 13, 17, … ఇలా ప్రధాన సంఖ్యలు అనంతం. ప్రతి సంఖ్యా ప్రధాన సంఖ్య కానీ, ప్రధాన సంఖ్యల గుణిత ఫలం గానీ అయి ఉండాలి. ఉదాహరణకి, 14 ప్రధాన సంఖ్య కాదు; దానిని 2 x 7 గా రాయవచ్చు. ఈ మాత్రం పరిచయంతో ప్రధాన సంఖ్యల గురించి చిన్న పిల్లలకి కూడ అర్థమయే ప్రశ్నలు వెయ్యవచ్చు. వాటిలో కొన్నిటికి తలపండిన మేధావులు కూడా సమాధానం చెప్పలేరు!

ఉదా: రెండు మూడు వందల సంవత్సరాల క్రితం గోల్డ్‌బాఖ్ (Christian Goldbach) అన్నాయన ఇది ప్రతిపాదించాడు: రెండు కన్నా మించిన ప్రతి సరి సంఖ్యా, రెండు ప్రధాన సంఖ్యల కూడికకి సమానం. దీనిని గోల్డ్‌బాఖ్ వితర్కం (Goldbach Conjecture) అంటారు. కొన్ని ఉదాహరణలు: 4 = 2 + 2; 6 = 3 + 3; 8 = 3 + 5; 10 = 5 + 5; 12 = 5 + 7; 14 = 7 + 7; 16 = 5 + 11. కాని ఎన్ని ఉదాహరణలయినా వివరించడానికే కాని ప్రతిపాదనని రుజువు చెయ్యలేవు. అనంత మయిన సరి సంఖ్యలలో ఏ రెండు ప్రధాన సంఖ్యలని కలిపినా రాని దేదన్నా దాగి ఉండవచ్చు. అలాంటి సరి సంఖ్య లేదు అని రుజువు చేసిందాకా ఇది కేవలం ప్రతిపాదన మాత్రమే, సిద్ధాంతం కాదు. ఇప్పటికీ ఇది ఎవరికీ కొరుకు పడని సమస్య!

అలాంటిదే మరొకటి. ఈ జంట సంఖ్యలని చూడండి: (3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), … ఇలాంటి జంటలు – జంటలోని రెండూ ప్రధాన సంఖ్యలే, వాటి మధ్య తేడా రెండు – అనంతంగా ఉన్నాయని చాలా కాలం క్రితమే ప్రతిపాదించారు. దీనినే ప్రధానసంఖ్యాజతి వితర్కం (twin prime conjecture) అంటారు. కాని గొప్పగొప్ప వాళ్ళెంత కష్టపడినా ఇంతవరకూ దీనిని ఎవరూ రుజువు చెయ్యలేకపోయారు!

కాని హిల్బర్ట్ ప్రసంగం నాటికి, ఇలాంటి ప్రతిపాదనలని ఎప్పుడో ఒకప్పుడు గణితవేత్తలు అటో ఇటో తేల్చగలరనుకున్నారు. ఎప్పటికీ తేలని సమస్యలంటూ సంఖ్యాగణితంలో లేవని హిల్బర్ట్‌తో పాటు మిగిలిన గొప్ప గణితవేత్తలంతా నమ్మారు. అంటే సంఖ్యా గణితం సంపూర్ణమని వారి నమ్మిక.

సంఖ్యా గణితంలో వైరుధ్యాలకి తావు లేదని అందరూ నమ్మారు. అంటే సంఖ్యా గణితం లోని సూత్రాలు క్రమంగా ఏ వరుసలో వాడినా, ఎన్నటికీ అవి వైరుధ్యానికి దారితీయలేవు. వైరుధ్యరహితం అంటే, సంఖ్యా గణిత సూత్రాలను ఎలా వాడుకున్నా ఎప్పటికీ ౦ ≠ ౦ (సున్నా సున్నాకి సమానం కాదు) అని నిరూపించడానికి వీలు కాదన్నమాట.

విజ్ఞానశాస్త్రాలలో కెల్లా మకుటాయమైనది గణితశాస్త్రం. దాంట్లోకెల్లా మౌలికమైనది సంఖ్యాగణితం. సంపూర్ణం, వైరుధ్యరహితం, అన్నది నమ్మిక మాత్రమే. దానికి సిద్ధాంతపరమైన రుజువు కనుక్కోమని హిల్బర్ట్ గణితవేత్తలకి సవాలు విసిరాడు. గత శతాబ్దారంభంలో హిల్బర్ట్ చేసిన ప్రముఖ ప్రసంగంలో ఇచ్చిన సమస్యలలో ఇది రెండోది. ఇంతకన్నా పేరున్న సమస్య ఇంకేముంటుంది? గూడెల్ దానినే ఎంచుకున్నాడు.

ఎంచుకున్న సంవత్సరానికే, కాంట్, హిల్బర్ట్‌ల జన్మస్థానమైన కోనిగ్స్‌బర్గ్ పట్టణంలో 1930 సెప్టెంబరులో జరిగిన ఓ సమావేశానికి గూడెల్ హాజరయ్యాడు. ఓ రౌండ్ టేబిల్ చర్చలో గూడెల్ దాదాపు అనాలోచితంగా, “గణితంలో గోల్డ్‌బాఖ్ ప్రతిపాదన లాంటివే కొన్ని వాస్తవమైనా నిరూపించలేనివి ఉన్నాయి”, అన్నాడు. దాని అర్థం సంఖ్యా గణితం అసంపూర్ణం అని!

మరునాడు, అదే నగరంలో, హిల్బర్ట్ తన గౌరవార్థం చేసిన సభలో ఇచ్చిన ప్రఖ్యాత ప్రసంగంలో “రుజువు చెయ్యలేని సమస్యంటూ లేదు”, అని ఉద్ఘాటించాడు. గూడెల్ బహుశా ఆ ప్రసంగం వినే ఉంటాడు. కాని మెదలకుండా ఊరుకున్నాడు. 1931 మార్చి 25న గూడెల్ ‘On Formally Undecidable Propositions of Principia Mathematica and Related Systems’ అన్న తన పేపరుని ప్రచురించాడు. దాని పిడుగుపాటు పర్యవసానాల్ని గణిత ప్రపంచం గుర్తించడానికి కొంత సమయం పట్టింది. గూడెల్ నిరూపణా విధానం అందరినీ విస్మయపరచింది. సూక్ష్మాలు తెలుసుకున్న పిదప, గూడెల్ సాధించినది విప్లవాత్మకమైనదనీ, అతని పేపర్ తార్కిక గణితానికే మైలురాయి అనీ, చారిత్రాత్మకమైనదనీ గుర్తించారు. అది రాసేనాటికి గూడెల్‌కి పాతికేళ్ళు కూడా నిండలేదు!

ఈ పేపర్ మూలంగా గూడెల్ పేరు గణిత ప్రపంచంలో నలుమూలలా ప్రాకింది. అమెరికాలో కొన్ని యూనివర్సిటీలు సందర్శించమని గోడెల్కి ఆహ్వానాలు పంపాయి. వాటిల్లో యూనివర్సిటీ కాకపోయినా విశిష్టమైన విద్యా సంస్థ ఇన్స్టిట్యూట్ ఆఫ్ అడ్వాన్స్డ్ స్టడీ (IAS). ఇప్పుడు కూడా ఈ సంస్థని గణితంలో ప్రపంచంలో కెల్లా అగ్రగామి సంస్థగా గుర్తిస్తారు. అంతేకాక ప్రపంచంలోకెల్లా మొట్టమొదటగా నిర్మించిన కంప్యూటర్లలో ఒకదానికి అక్కడే అంకురార్పణ జరిగింది.

ఇన్స్టిట్యూట్ ఆఫ్ అడ్వాన్స్డ్ స్టడీ (IAS)

వంద సంవత్సరాల క్రితం, అమెరికాలో ఆధునిక వైద్యం పేరిట బూటకం సాగుతుండేది. కేవలం డబ్బు సంపాదించడం కోసం కుప్పలు తెప్పలుగా వైద్య కళాశాలలు నెలకొల్పారు. కార్నగీ ఫౌండేషన్ దేశంలోని వైద్యవిద్య బాగోగులని పరిశీలించమని అబ్రహం ఫ్లెక్స్‌నర్ అన్న విద్యావేత్తని కోరింది. ఆయన దేశంలోని నూటయాభయి పైగా ఉన్న వైద్య కళాశాలలని సందర్శించి, ఓ కటువైన నివేదిక(Flexner Report)సమర్పించాడు. వైద్య విధానాన్నీ, బోధనా పద్ధతుల్నీ క్షాళన చెయ్యవలసిన అవసరం ఉందంటూ తీవ్ర పదజాలంతో అప్పటి వైద్యవిద్యని విమర్శించాడు. వైద్యం శాస్త్రీయ పద్ధతులలో నేర్పాలనీ, జబ్బుల గురించీ, రోగుల గురించీ, వైద్యం గురించీ శాస్త్రీయమైన పరిశోధన జరగాలనీ, వైద్యులు కాదలచుకున్న వాళ్ళు కనీసం ఆరేళ్ళ పాటు కాలేజీ విద్య నభ్యసించాలనీ, వైద్య విద్యా ప్రమాణాలు ఎలా పెంచాలో వివరంగా చర్చించాడు. ఆ నివేదిక మూలంగా అనతి కాలంలో దాదాపు అన్ని వైద్య కళాశాలలూ మూసివేశారు. నూతన వైద్య విద్యా విధానాలతో కొత్త కళాశాలలని స్థాపించారు. ఇప్పుటికీ ఫ్లెక్స్‌నర్ ప్రవేశపెట్టిన విధానాల ననుసరించే అమెరికాలో వైద్య విద్యాబోధన చేస్తారు. ఆధునిక వైద్యంలో ప్రపంచంలోకెల్లా అమెరికా అగ్రస్థానంలో ఉండటానికి ముఖ్య కారణం ఫ్లెక్స్‌నర్ నివేదికే అనంటే అతిశయోక్తి కాదు.

అదే కాలంలో లూయిస్ బాంబర్గర్ అని ఒక వ్యాపారస్తుడు న్యూజెర్సీ రాష్ట్రంలోని నువార్క్ నగరంలో దివాలా తీస్తున్న ఓ దుకాణాన్ని వేలంపాటలో కొని దక్షతతో వృద్ధిలోకి తెచ్చాడు. చుట్టుపక్కల దానికి మంచి డిపార్ట్‌మెంటల్ స్టోరుగా పేరొచ్చింది.; వ్యాపారం రాణించింది. వ్యాపారంలో భాగస్తుడు సొంత చెల్లెలి భర్తే. భర్త చనిపోవడంతో వ్యాపారాన్ని అమ్మేయాలని చెల్లెలు, క్యారలైన్ బాంబెర్గర్ ఫల్డ్, తీర్మానించుకుంది. వారి అదృష్టం బావుంది; 1929లో, స్టాక్ మార్కెట్ మరో ఆరు వారాలలో కూలిపోతుందనగా, మేసీ కంపెనీ (Macy’s) బాంబెర్గర్ స్టోరుని పాతిక మిలియన్ డాలర్లకి కొన్నది. బాంబెర్గర్లు అనేక సేవాకార్యాలకి విరాళాలిచ్చేవారు. తమ డబ్బులో 15 మిలియన్ల డాలర్ల విరాళంతో ఓ వైద్య కళాశాలని స్థాపించాలని నిర్ణయించుకున్నారు. ఫ్లెక్స్‌నర్ తల్లిదండ్రులు జర్మనీ నుండి అమెరికాకి వలస వచ్చిన యూదులు. మిగిలిన యూదులతో వాళ్ళకి దగ్గర సంబంధాలుండేవి. బాంబెర్గర్ల స్నేహితుడొకరు వాళ్ళకి ఫ్లెక్స్‌నర్‌ని పరిచయం చేశాడు. ఫ్లెక్స్‌నర్ అప్పటికే అమెరికాలో ఉన్నత విద్య, పరిశోధనల గురించి ఆలోచనలు చేస్తున్నాడు; ఆదర్శప్రాయమైన ఆశయాలు పెంచుకున్నాడు. తను కన్న కలలు నిజం కావాలంటే, ఓ కొత్తరకమైన విద్యాసంస్థని నెలకొల్పడమే మార్గమని నిశ్చయించుకున్నాడు. వైద్యకళాశాల కంటే అది ఉన్నతమైనదనీ, వారి విరాళం సార్థకమవుతుందనీ బాంబెర్గర్లని ఒప్పించాడు.

ఆ సంస్థలో ప్రపంచంలో ఎక్కడినుండయినా మేధావులు వచ్చి చేరవచ్చు. పాఠాలు చెప్పక్కర్లేదు; రోజువారీ పరిపాలనా బాధ్యతలు చేపట్టనవసరం లేదు; వారు చెయ్యాల్సిందల్లా, వాళ్ళకి చేతనయిన ఒకే ఒక పని – ఆలోచించడం. అది పాండిత్యానికి పెట్టినిల్లు కావాలి. దాతలు నగరానికి దగ్గరలో పెట్టాలని కోరారు. కాదు, నగరానికి దూరంగా, ప్రశాంత వాతావరణమున్న ప్రిన్స్టన్ పట్టణమే తగిన చోటని ఫ్లెక్స్‌నర్ నచ్చజెప్ఫాడు. ఆవిధంగా ఇన్స్టిట్యూట్ ఆఫ్ అడ్వాన్స్డ్ స్టడీ (IAS) మొదలయింది.

విజ్ఞానశాస్త్రాలలో కెల్లా గణితం చవకైనది – పెద్ద పెద్ద ప్రయోగశాలలూ, ఖరీదైన పరికరాలూ అవసరం లేదు; కలమూ కాగితమూ చాలు. అలాగే అభ్యర్థులని ఎంచుకోవడం కూడా తేలిక – ఎవరు గొప్పవాళ్ళు అన్నదాని మీద ఏకాభిప్రాయం మిగిలిన శాస్త్రాలలో కన్నా గణితంలోనే సులువు అని ఫ్లెక్స్‌నర్ భావించాడు. అందువలన మొదట ఏర్పరిచినది గణిత విభాగమే. పెట్టిన కొద్దికాలంలో ఐన్స్టయిన్ వచ్చి చేరడంతో సంస్థకి ప్రతిష్ఠ వచ్చింది. అదే సమయంలో హిట్లర్ ధాటికి తట్టుకోలేక అనేక మంది మేధావులు యూరప్ వదిలి పారిపోతున్నారు. వాళ్ళలో అనేకమంది ప్రముఖులకి I.A.S నీడనిచ్చింది. వేల్ (Weyl), ఫాన్ నోయ్‌మన్ (von Neumann) – వారిలో కొందరు. అక్కడకే గూడెల్ కూడా ముందర స్కాలర్ హోదాలో తాత్కాలికంగా వచ్చాడు.

కాని 1939లో గూడెల్ తిరిగి వియన్నా చేరేటప్పటికి అక్కడి రాజకీయ పరిస్థితులు బాగా విషమించాయి. నగరం నాజీల వశమయింది. హిట్లర్ పాతపద్ధతులను రద్దు చేసి కొత్త నిబంధనలు పెట్టాడు. వాటిలో భాగంగా గూడెల్ ఉద్యోగం ఊడింది. కొత్తగా దరఖాస్తు పెట్టుకున్నాడు. దానిని అధికారులు వెంటనే మంజూరు చెయ్యలేదు. కారణం – అధికారులు సందిగ్ధంలో పడడం; గూడెల్ నాజీలకి వ్యతిరేకంగా ఎప్పుడూ ఏమీ మాట్లాడలేదు కాని, గూడెల్ పీహెచ్. డీ ఓ యూదు కింద చేశాడు. మరి గూడెల్‌ని నమ్మాలా? వద్దా?!

ఓ రోజు నాజీ రౌడీలు గూడెల్‌ని బజారులో పట్టుకుని దౌర్జన్యం చేశారు – గూడెల్ యూదుల సహచరుడని. వాళ్ళావిడ దుండగులని తరిమి కొట్టవలసి వచ్చింది. అప్పుడిక వియన్నాలో ఉండకూడదని నిర్ణయించుకొని IASకి వస్తానని అక్కడి వాళ్ళకి తెలియ చేశాడు. ఇంత జరిగినా, గూడెల్‌కి నాజీల దుర్మార్గం గురించి ఏమీ అవగాహన ఉన్నట్లు లేదు; నాజీల మూలంగా యూదులు పడిన బాధల గురించి సున్నితంగా మాట్లాడినవాడు కాదు.

వియన్నా వదలాలంటే, జర్మనీ అధికారులు అనుమతి ఇవ్వాలి. అమెరికా రావడానికి అమెరికా ప్రభుత్వం వీసా ఇవ్వాలి. రెండూ కష్టమే. అమెరికా ప్రభుత్వానికి, గూడెల్ ప్రొఫెసరు కాకపోయినా, అలా నిజాన్ని కాస్త సాగదీసి చెప్పి, జర్మనీ వాళ్ళకి గూడెల్ మేధావి వర్గానికి చెందిన ఆర్య జాతీయుడు కావడం వల్ల యుద్ధం చెయ్యడం కంటె పరిశోధనలు చేస్తే మంచిదని, మొత్తానికి IAS అధికారులు రెండు ప్రభుత్వాలనీ ఒప్పించారు. చివరకి గూడెల్, అట్లాంటిక్ మీదుగా వస్తే ఇంగ్లాండు వాళ్ళు జర్మనీవాడని పట్టుకుంటారేమోనని, రష్యా, జపానుల వైపుగా దీర్ఘ ప్రయాణం తర్వాత భార్యతో సహా అమెరికా చేరుకున్నాడు – 1940 మార్చిలో. మరలా అతను యూరపులో అడుగుపెట్టలేదు!

అమెరికా జీవితం

భాష కొత్త, దేశం కొత్త. గూడెల్, అడేల్ కొద్ది మంది మిత్రులతో తప్ప చుట్టుపక్కల వాళ్ళతో పెద్ద స్నేహ సంబంధాలు పెంచుకోలేదు. గూడెల్ స్వతహాగా ఒంటరితనాన్ని అభిమానించే రకం. ఆడెల్ నోటి దురుసుతో, అధికారం చలాయించే రకం. ఆవిడ కుటుంబం వైపు వాళ్ళకి కాన్సర్ రావడాన, తమకు పిల్లలు వద్దని గూడెల్ కోరుకున్నాడు. ఆమెకి పిల్లలు లేని లోపం బాధగా ఉండేది. కాని గూడెల్ జీవితానికి కావలసిన సంరక్షణ ఇచ్చింది. అతను తన పరిశోధనలలో నిమగ్నం కావడానికి కావలసిన వాతావరణం కల్పించింది. అతని అవసరాలు తీర్చి ఆదరణతో చూసింది.

గూడెల్, ఐన్‌స్టయిన్ (1950లో)

వచ్చిన రెండేళ్ళలో గూడెల్, ఐన్‌స్టయిన్ మంచి స్నేహితులయ్యారు. వారిద్దరూ విభిన్నవ్యక్తిత్వాలు కలవాళ్ళు. ఐన్‌స్టయిన్ కలగలపుగా, నవ్వుతూ తుళ్ళుతూ ఉండేవాడు. గూడెల్ ఒంటరి, సీరియస్ మనిషి; ఇతరులని నమ్మేవాడు కాడు. గూడెల్‌కి గణితం మినహా బయట ప్రపంచంలో ఎలా వుండాలో సరిగా తెలియదు. ఐన్‌స్టయిన్ అది గుర్తించి అవసరమైన సాయం చేసేవాడు.

గూడెల్ అమెరికా పౌరసత్వపు ఇంటర్వ్యూ కెళ్ళే ముందర, అందరిలాగే, అమెరికా ప్రభుత్వం గురించీ, రాజ్యాంగం మీదా చదువుకుని పరీక్షకు తయారయ్యాడు. గూడెల్ ఏ పని చేసినా క్షుణ్ణంగా చేసేవాడు. అమెరికా రాజ్యాంగాన్ని కూలంకషంగా చదివాడు. దాంట్లో ఓ తార్కిక అసంబద్ధత కనుక్కున్నాడు! ఇక దాని గురించే మధనపడటంతో మిత్రులకి ఆందోళన కలిగింది – ఇంటర్వ్యూలో ఏం చెప్పి, అనవసరంగా ఏ గొడవలో ఇరుక్కుంటాడోనని. గూడెల్ మనసు వేరే దాని మీద మరల్చడానికి ఐన్‌స్టయిన్ తోడుగా వెళ్ళి శతవిధాలా ప్రయత్నించాడు. చివరకి జడ్జి గోడెల్ని, “యూరప్ లో వచ్చినట్లు అమెరికాలో కూడా నియంతృత్వం వచ్చే అవకాశం ఉందా?” అని అడిగాడు. “ఎందుకు లేదు?”, అంటూ గూడెల్ అమెరికా రాజ్యాంగంలో ఉన్న అసంబద్ధత దానికెలా దారితీయవచ్చో వివరించ పూనుకున్నాడు. అంతకు ముందు ఐన్‌స్టయిన్‌కి కూడా ఆ జడ్జే పౌరసత్వం ప్రదానం చెయ్యడాన, ఆయన కనుసైగల మూలంగా గూడెల్ విపరీత స్వభావం అర్థమయి, అంతటితో పోనిచ్చి పౌరసత్వం ఇచ్చాడు.

గూడెల్‌కి IASలో చాలా కాలం ప్రొఫెసరు పదవి లభించలేదు. తగిన గుర్తింపు రానందుకు గూడెల్ కొంతకాలం డిప్రెషన్‌కి లోనయ్యాడు. అతనికి ఆహారం విషయంలో జీర్ణ సమస్యలుండేవి. దానికితోడు పరులు తనమీద కుట్రలు పన్నుతున్నారనీ, ఇంట్లో దొంగలు పడ్డారనీ, దెయ్యాలున్నాయనీ, ఇలా అనేక భ్రమలు పెంచుకొని అనారోగ్యం పాలయ్యేవాడు. ఒకసారి ఆసుపత్రిలో ఉండగా అతని గురించి ఆందోళన పడిన IAS డైరెక్టరు ఆపెన్‌హైమర్, గూడెల్‌ని ఉత్తేజపరచాలంటే ఏం చెయ్యాలి అని ప్రశ్నిస్తే, ప్రొఫెసరు పదవి ఇవ్వాలని మిత్రులు సూచించారు. గూడెల్ ప్రొఫెసరు కాకుండా, మనం ప్రొఫెసర్లు గావడం సిగ్గుపడాల్సిన విషయం అని ఫాన్ నోయ్‌మన్ అంతటి వాడే అన్నాడు. అయితే అకడెమిక్ గొడవల మూలానా, గూడెల్‌కి పాలనా బాధ్యతలు తెలియవనీ కొందరు విముఖత చూపారు. అప్పుడు, ఆపెన్‌హైమర్‌కి ఓ ఆలోచన వచ్చింది.

ఐన్‌స్టయిన్ పేరు మీద అవార్డు ఇచ్చే కమిటీలో ఆపెన్‌హైమర్, గూడెల్ మిత్రులు – ఐన్‌స్టయిన్, ఫాన్ నోయ్‌మన్, సభ్యులు. ముందర మిత్ర పక్షపాతమనిపించినా, గూడెల్ సాపేక్ష శాస్త్రంలో చేసిన పరిశోధనలకి తగినవాడేనని నిర్ధారించుకున్నారు. అయితే అప్పటికే వేరేవారికివ్వాలని (Julian Swinger) నిర్ణయించుకున్నారు. చివరకి, ఇద్దరికీ ఇవ్వాలని నిశ్చయించడంతో గూడెల్‌కి శాస్త్ర సమాజంలో గుర్తింపు లభించింది. దాని మూలంగా కొంత డబ్బు కూడా వచ్చింది. ఆపెన్‌హైమర్ ఆశించినట్లుగానే, గూడెల్ ఉత్సాహభరితుడయ్యాడు.

గూడెల్ విశ్వశాస్త్రం (Cosmology) మీదా, ఫిలాసఫీ మీద రచనలు చేశాడు. లైబ్నిట్జ్(Leibniz) అంటే మక్కువ చూపాడు. కాని లైబ్నిట్జ్ రచనలు ప్రచురించకుండా ఎవరో కుట్ర పన్నారని ఆరోపించాడు! ఎప్పుడూ ఏదో ఒకదాని మీద గూడెల్‌కి అనుమానంగా ఉండేది.

విషాదంలో ముగిసిన జీవితం

రిటైర్మంట్ వయసు దగ్గరపడేటప్పటికి, గూడెల్ మానసిక ఆరోగ్యం బాగా దెబ్బతిన్నది. ఐన్‌స్టయిన్, ఫాన్ నోయ్‌మన్‌ల మరణంతో తనకి చేదోడు వాదోడుగా ఉన్న కొద్దిమంది మిత్రులనూ కోల్పోయాడు. డిప్రెషన్ పెరిగింది. భార్యనీ, ఒక మిత్రుడినీ తప్ప ప్రతివాళ్ళనీ అనుమానించడం మొదలెట్టాడు – తనని చంపడానికి ప్రయత్నిస్తున్నారని! డాక్టర్లను అసలే నమ్మేవాడు కాడు. తీసుకునే ఆహారం చాలా తగ్గిపోయింది. తినే ప్రతిదీ, భార్య రుచి చూసి ఇస్తే గాని తినేవాడు కాదు. దాంట్లో ఎవరైనా విషం పెట్టారేమోనని భయం! ఇంతలో భార్య అనారోగ్యం పాలయి ఆసుపత్రిలో చేరింది. గూడెల్‌కి నమ్మకంగా సేవ చేసేవాళ్ళు లేరు. ఆహారంలో విషం పెట్టారేమోనని శంకతో పస్తులుండేవాడు. మనిషి చిక్కి శల్యమయ్యాడు. ఆకృతి అస్థిపంజరంలా తయారయింది. భార్య వత్తిడితో ఆసుపత్రిలో చేర్చేటప్పటికి బాగా ఆలస్యమయింది. డాక్టర్లు చెయ్యగలిగిందేమీ లేదు. అలా తన మానసిక రుగ్మతల మూలంగా, తన శరీరాన్ని తనే హింసించుకొని, గత శతాబ్దపు గొప్ప మేధావులలో ఒకడైన గూడెల్ 1978 జనవరి 14న చనిపోయాడు. మరో రెండేళ్ళకి భార్య కూడా మరణించింది.

స్ఫూర్తినిచ్చిన వితర్కాలు

హిల్బర్ట్ పథకం సంఖ్యా శాస్త్రం సంపూర్ణమనీ, వైరుధ్య రహితమనీ రుజువు చెయ్యడం. గూడెల్ అది అసాధ్యమని రుజువు చేశాడు! అందుకు అతనికి రెండు పారడాక్సులు దోహదం చేశాయి.

అసత్యవాది వితర్కం (Liar’s Paradox)

రెండువేల సంవత్సరాల క్రితం గ్రీకులు గణితంలో అద్భుతమైన ఆలోచనలు చేశారు. మనం చిన్నప్పుడు చదువుకున్న రేఖాగణితం వాళ్ళదే. ఆ కాలంలోనే కొందరు గ్రీకులు నిత్యజీవితంపై వాదోపవాదనలు చేసి అబ్బురపరచేవారు. వారిలో తిమ్మిని బమ్మి, బమ్మిని తిమ్మి చేసేవారని సోఫిస్టులకి పేరు వచ్చింది. ఆ వాదనలలో కొన్ని వైరుధ్యాలు ఇబ్బంది కలిగించేవి. జీనో పారడాక్స్ గురించి ఇంతకుమునుపు ఒక వ్యాసంలో చెప్పాను. ఆ కాలంలోనే వచ్చిన మరో పారడాక్స్ అసత్యవాది వితర్కం. దాని గురించి బైబిల్లో ఒకచోట, సెయింట్ పాల్ అంటాడు: One of themselves, a prophet of their own, said, “Cretans are always liars, wily beasts, lazy gluttons”. This testimony is true. [Titus I: 12-13].

సెయింట్ పాల్ ఆ వాక్యంలోని తర్కాన్ని గుర్తించాడో లేదో కాని అదే వాక్యం రెండు వేల సంవత్సరాల తర్వాత కూడా తార్కిక గణితాన్ని ప్రభావితం చేసింది. పై వైరుధ్యాన్ని ఈ చిన్న వాక్యం ద్వారా గ్రహించవచ్చు: “ఈ వాక్యం అబద్ధం” అన్నది నిజమైతే, తన గురించి తను చెప్పుకున్నది నిజమన్న మాట; మరి తన గురించి తను ఏం చెప్తున్నది? తను అబద్ధమని! పోనీ, ఈ వాక్యం అబద్ధం అనుకుందాం. అంటే తనను గురించి తను చెప్తున్నది అబద్ధం; ఆ మాటేగదా ఆవాక్యం చెప్పేది. అంటే ఆ వాక్యం నిజం!

ఆ వాక్యం నిజమనుకుంటే అబద్ధమనీ, అబద్ధమనుకుంటే నిజమనీ తేలుతున్నది! అదీ వైరుధ్యం. మనం నిత్య జీవితంలో వాడే భాషలో ఇలాంటి వైరుధ్యాలున్నాయి. కానీ గణితంలో ఇలాంటి వైరుధ్యాలుంటే మొత్తం గణిత వ్యవస్థే కుప్పకూలిపోతుంది.

రిచర్డ్ వితర్కం (Richard Paradox)

1905 లో జూల్స్ రిచర్డ్ (Jules Richard) సంఖ్యాగణితానికి సంబంధించిన ఓ పారడాక్స్ని కనుక్కున్నాడు. సంఖ్యల్లో అనేక గుణాలున్నాయి. ప్రతి గుణానికీ ఓ పేరు పెట్టి, వాటినన్నిటినీ తెలుగు వరుసలో రాద్దాం:

    1     ప్రధాన (Prime)
    2     బేసి (Odd)
    3     వర్గ (Cube)
    4     సరి (Even)
    5     సంయుక్త (Composite)
    6     …
    7     …

పట్టికలో ప్రతి గుణానికీ దాని స్థానాన్ని బట్టి ఓ విలువ ఉంటుంది; దానిని గుణానికి ఎడమ వైపున సంఖ్యగా గమనించండి. ఉదాహరణకి, వర్గ గుణం మూడో స్థానంలో ఉంది. అయితే స్థాన విలువ కూడా ఒక సంఖ్యే కదా. ఆ సంఖ్యకి ఆ పట్టిక వరుసలోని గుణం ఉండొచ్చు, లేకపోవచ్చు. ఇప్పుడు మనమో కొత్త గుణాన్ని, రిచర్డ్ గుణాన్ని, నిర్వచిద్దాం: స్థాన విలువ సంఖ్యకి పట్టిక వరుసలోని గుణం లేకపోతే ఆ సంఖ్యని రిచర్డ్ సంఖ్య అని పిలుద్దాం. పై పట్టికలో 2 రిచర్డ్ సంఖ్య, ఎందుకంటే 2 బేసి సంఖ్య కాదు కనుక.

అన్ని గుణాలూ పట్టికలో రావాలి కనుక రిచర్డ్ గుణం కూడా ఈ పట్టికలో ఎక్కడో ఒకచోట, నిఘంటువు వరుస ప్రకారం, రావాలి. ఆ స్థాన విలువని N అనుకుందాం. ఇప్పుడో ప్రశ్న: N రిచర్డ్ సంఖ్యా? కాదా?

అది రిచర్డ్ సంఖ్య అయితే, ఆ స్థానంలోని గుణం దానికి ఉండకూడదు. కాని ఆ గుణం రిచర్డ్ గుణం. అంటే, అది రిచర్డ్ సంఖ్య అయితే దానికి రిచర్డ్ గుణం లేదు, అంటే అది రిచర్డ్ సంఖ్య కాదు! అది రిచర్డ్ సంఖ్య కాకపోతే, ఆ స్థానంలోని గుణం దానికుండాలి, కాని ఆ గుణం రిచర్డ్ గుణం; అంటే అది రిచర్డ్ సంఖ్య!

N రిచర్డ్ సంఖ్య అయితే కాదనీ, కాదంటే అవుననీ తీర్చాం!ఈ వైరుధ్యానికి కారణం ఏమిటి? సంఖ్యల గుణాల గురించి మాట్లాడుతూ, కొత్త గుణం – సంఖ్యలకి సంబంధించనిది, గుణాల స్థానానికి సంబంధించిన గుణాన్ని తీసుకొచ్చి – కలిపి మాట్లాడటం ఈ వైరుధ్యానికి కారణం.

ఈ పారడాక్సులు రెండిటినీ దృష్టిలో ఉంచుకొని వాటికన్నా పకడ్బందీగా వైరుధ్యాలు లేని ఓ ఫార్ములాని తయారుచేశాడు గూడెల్.

గూడెల్ అసంపూర్ణ సిద్ధాంత సారాంశం

గూడెల్ నిరూపించిన విధానం విశిష్టమైనది; అసలు అది నిరూపణేనా అని అనుమానం కలిగించేది. విశదంగా చూస్తే అది గూడెల్ మేధకి అద్దం పట్టి అబ్బురపరచేది. గూడెల్ నిరూపణని అంచెలంచెలుగా చెప్పడానికి ప్రయత్నిస్తాను. సైన్సు వ్యాసాలలో సంకేతాలూ, సమీకరణాలూ ఉంటే పాఠకులు చదవరని అందరిలాగే నాకూ భయం. ముందర, మరీ లోతుల్లోకి వెళ్ళకుండా గూడెల్ నిరూపణ చూచాయగా చెప్తాను. తర్వాత కాస్త నిర్దుష్టంగా విపులీకరిస్తాను – కొందరికైనా కుతూహలం పెరిగి వ్యాసం చివర ఇచ్చిన పుస్తకాలని సంప్రదిస్తారని నా ఆశ.

ఫార్ములాల భాష ఒకటుందనుకోండి. దాంట్లోని ఫార్ములాలలో ఒకటి: ‘ఈ ఫార్ములాని నిరూపించలేము’. ఇది ఓ సామాన్య వాక్యం కదా, ఫార్ములా ఎలా అవుతుంది అని అనుమానం వచ్చిందా? ప్రస్తుతానికి ఫార్ములా అంటే కొన్ని సంకేతాల సముదాయం అనుకోండి. అసత్యవాది వైరుధ్యంలోని వాక్యానికీ, దీనికీ గల తేడా గమనించండి. నిజమా కాదా అనకుండా, నిరూపించగలమా లేదా అని వాడదాం.

1. పై వాక్యం నిజమైతే, మనం నిరూపించలేని ఫార్ములాలు కొన్ని (కనీసం ఒకటి) ఉన్నాయి.
2. పై వాక్యం అబద్ధమైతే, ఆ ఫార్ములాని నిరూపించగలం.
3. ఫార్ములాని నిరూపించగలిగితే, ఆ వాక్యం అబద్ధం.
4. ఫార్ములాని నిరూపించలేకపోతే, ఆ వాక్యం నిజం.

నిజమైతే నిరూపించలేం; నిరూపించలేకపోతే, నిజం! True if and only if not provable. ఇంతకు మునుపటి పారడాక్స్ల లాగా దీంట్లో వైరుధ్యమేమీ లేదు. కాని ఈ వాదన ప్రకారం, నిరూపించలేని నిజాలున్నాయి!

ఇది హిల్బర్ట్ పథకానికి గొడ్డలిపెట్టు. కాని పై వాదన చూచాయగా ఉందేకాని నిర్దిష్టంగా లేదు; దానిని నిరూపణగా గణితవేత్తలు ఒప్పుకోరు. అయితే గూడెల్ చాలా కట్టుదిట్టంగా నిరూపించాడు. అతని పేపర్లు చదవడానికి కష్టమయినా, ఎంతో జాగ్రతగా రాసినవి; కరాఖండితంగా ఉంటాయి; స్పష్టతకీ, శ్రద్ధకీ మచ్చుతునకలు. ఇప్పుడు ఇంకాస్త లోతుగా గూడెల్ నిరూపణని పరిశీలిద్దాం.

మూడు వేర్వేరు భాషలు

గూడెల్ సిద్ధాంతాలని సరిగా అర్థం చేసుకోవడానికి ముందర మూడు రకాలైన భాషల గురించి స్పష్టమైన అవగాహన ఉండాలి:

1. క్రమబద్ధ సంఖ్యాగణితం (Formal Arithmetic or FA): ఇది క్రమబద్ధమైన భాష. కొన్ని సంకేతాలతో వ్యాకరణాన్ని పోలిన సూత్రాలతో దీంట్లో వాక్యాలని (ఫార్ములాలని) యాంత్రికంగా రూపొందించవచ్చు. ఈ భాషలోని వాక్యాలకి అర్థం లేదు. అర్థం కావాలంటే చెప్పుకోవచ్చు. కాని ప్రస్తుతానికి అది కేవలం కొన్ని సూత్రాల ప్రకారం నడిచే భాష అనీ, రూపమే కాని సారం లేని భాష అనీ గుర్తుంచుకోండి. ఉదాహరణ: S0 + SS0 = SSS0. ఇది కేవలం S, 0, +, = అన్న సంకేతాలతో కూడిన పద బంధం గల వాక్యం (ఫార్ములా).
2. ఆధిసంఖ్యాగణితం (Meta Arithmetic or MA): FA భాషలోని సంకేతాల, వాక్యాల మధ్య సంబంధం గురించి ఈ భాషలో మాట్లాడుకోవచ్చు. ఉదాహరణ: ‘S0 + SS0 = SSS0’ అన్న ఫార్ములాలో మొదటి సంకేతం ‘S’.
3. ప్రాథమిక సంఖ్యాగణితం (Informal Arithmetic or IA): ఇది మనకందరికీ పరిచయమున్నది. సంఖ్యల మధ్య గల సంబంధాల గురించి ప్రతిపాదనలు చేస్తాం. కూడిక, హెచ్చవేతలు ఎలా చెయ్యవచ్చో చెప్పవచ్చు. ఉదాహరణ: 1 + 2 = 3.

క్రమబద్ధ సంఖ్యాగణితం (Formal Arithmetic or FA)

ఏ భాషకైనా మౌలికమైనవి అక్షరాలు. వాటినే సంకేతాలు, లేక గుర్తులు అంటారు. ఈ భాషలోని కొన్ని సంకేతాలు: ౦, S, (, ), =, +, ., ~. వీటిలో కొన్ని ఫార్ములాలలో చలనరాశులు (variables) ఉంటాయి. వాటిని x, y, z, … లతో సూచిద్దాం.

ఈ సంకేతాలను కలిపి ఫార్ములాలని తయారుచెయ్యవచ్చు. ఉదాహరణకి S0 + S0 = SS0. ఈ ఫార్ములాలు తయారుచెయ్యడానికి మార్గమేమిటి? కొన్ని పరిమితమైన ముందుగా నిర్ణయమైన ఫార్ములాలతో మొదలెట్టి క్రమమైన సూత్రాలతో ఆ ఫార్ములాలని మారుస్తూ కొత్త ఫార్ములాలని తయారు చెయ్యవచ్చు. ఈ భాషలో ముందరి ఫార్ములాలు ఇవి. వీటినే స్వయంసిద్ధ సూత్రాలు (Axioms) అంటారు:

పట్టిక 1. స్వయంసిద్ధ సూత్రాలు

ఫార్ములా సంఖ్య	స్వయంసిద్ధ సూత్రం
1	(∀x) ~Sx = 0
2	(∀x) (x + 0) = x
3	(∀x) (∀y) (x + Sy) = S (x + y)
4	(∀x) (x.0) = 0
5	(∀x) (∀y) (x.Sy) = ((x.y) + y)

ప్రస్తుతానికి ఈ ఫార్ములాల అర్థం పట్టించుకోకండి – FA భాషకి రూపమే గాని సారం లేదన్నాం కదా. వీటిని కేవలం సంకేతాల సముదాయంగా గుర్తుపెట్టుకోండి. ఈ ఫార్ములాలని క్రమబద్ధంగా మార్చడానికి ఈ క్రింది సూత్రాలు వాడుకోవచ్చు.

రూపాంతరీకరణ సూత్రాలు (Transformation Rules)

• ప్రత్యేక సూత్రం (Rule of Specification): (∀x) p అన్న ఫార్ములా నుండి, కేవలం p గల ఫార్ములాని గాని, p లో x చలనరాశికి బదులు మరేదైనా పదం వాడి కొత్త ఫార్ములాని గాని సృష్టించవచ్చు.
• సాధారణీకరణ సూత్రం (Rule of Generalization): p ఫార్ములాలో, x చలనరాశిగా ఉంటే, (∀x) p అన్న కొత్త ఫార్ములాని సృష్టించవచ్చు.
• మార్పిడి సూత్రం (Rule of interchange): ఈ రెండు పదబంధాలని, (∀x) ~ మరియు ~(∃x) ఒకదాని బదులు వేరే దానిని వాడి కొత్త ఫార్ములాని సృష్టించవచ్చు.
• అనురూప సూత్రం (Rule of Symmetry): p = q అన్న ఫార్ములాకి బదులు q = p వాడవచ్చు.
• సంక్రమణ సూత్రం (Rule of Transitivity): p = q అనీ q = r అనీ రెండు ఫార్ములాలు ఉంటే p = r అని వాడవచ్చు.

ఈ విధంగా మరికొన్ని సూత్రాలని నిర్వచించవచ్చు. అప్పుడు మనం పై స్వయంబద్ధ సూత్రాలతో మొదలెట్టి, ఈ రూపాంతరీకరణ సూత్రాలని వాడి కొత్త ఫార్ములాలని తయారుచేసుకోవచ్చు. ఉదాహరణకి ‘0 = 0’ అన్న ఫార్ములాని ఈ విధంగా రాబట్టవచ్చు. ప్రస్తుతానికి, ౦, =, ఈ రెండూ కేవలం అర్థంలేని గుర్తులు మాత్రమేనని గుర్తుంచుకోండి:

Step 1: (∀x) (x + 0) = x ; ఇది రెండో స్వయంసిద్ధ సూత్రం

Step 2: (౦ + ౦) = ౦ ; x కి బదులు 0 – ప్రత్యేక సూత్రం

Step 3: 0 = (0 + 0) ; అనురూప సూత్రం

Step 4: ౦ = ౦ ; సంక్రమణ సూత్రం – Steps 2, 3 ఆధారంగా

మరో ఉదాహరణ తీసుకుందాం:

Step 1: (∀x) ~Sx = 0 ; ఇది మొదటి స్వయంసిద్ధ సూత్రం

Step 2: ~S0 = 0 ; x కి బదులు 0 – ప్రత్యేక సూత్రం

ఇంతవరకు FA భాషలోని గుర్తులకి ఎలాంటి అర్థమూ ఆపాదించవద్దని చెప్పాను. కాని ఇప్పుడు ఆ సంకేతాలకి సామాన్య గణితపరమైన అర్థం ఇద్దాం. 0 అంటే సున్నా, + అంటే కూడిక, . అంటే గుణింతం, = అంటే సమానం, S అంటే Successor అలా. IA భాషలో మనకి తెలిసిన ౦ = ౦ అన్నదానికి సమతుల్యమైన FA ఫార్ములా ‘0 = 0’. IA భాషలో అయిదుని 5 గా సూచిస్తే, దానినే FA లో SSSSS0 గా, సున్నా ముందర అయిదుసార్లు S తో, సూచిస్తాం. IA భాషలో 1<> 0 అన్నదానికి FA భాషలో సమతుల్యమైనది ‘~S0 = 0’. దాని అర్థం – Not Successor of zero equals zero, అంటే Not one equals zero. (∀x అంటే for all x అనీ, ∃x అంటే there exists an x అనీ, ~ (టిల్డా) అంటే Not అనీ అర్థం చెప్పుకోవాలి.)

ముక్కు ఎక్కడుందో చూపమంటే, చెయ్యి తల వెనుక తిప్పి చూపెట్టినట్టు ఉంది కదూ. కాని ఇక్కడ రెండు ముఖ్య విషయాలని గమనించాలి. FA సంఖ్యాశాస్త్రాన్ని క్రమబద్ధం చేసేదే కాని, అది సంఖ్యాశాస్త్రం కాదు. అది కేవలం పద బంధాలని కొన్ని కచ్చితమైన సూత్రాల ద్వారా వేరే పద బంధాలుగా మారుస్తుంది. ఈ పద బంధాలని మనం సంఖ్యాశాస్త్రానికి అన్వయించి అర్థం తెలుసుకోవచ్చు, కాని FA కి సంబంధించినంతవరకు, అది పద బంధాలతో సంకేతాలని మారుస్తూ ఆడుకునే ఆట మాత్రమే.

సమన్వయ సహాయసిద్ధాంతం (Correspondence Lemma): సంఖ్యా గణితంలో కూడికలు, హెచ్చవేతలు, ప్రధాన సంఖ్యలు, మొదలైన వాటి గురించి అనంతమైన వాస్తవాలు ఉన్నాయి – ’10 సరి సంఖ్య’, ’21 ప్రధాన సంఖ్య కాదు’, ‘ఏడో ప్రధాన సంఖ్య 17’, ఇలా. వీటిని ప్రాధమిక పునరావృత్త సత్యాలు (primitive recursive truths) అంటారు. ప్రాధమిక పునారావృత్త అంటే స్థూలంగా ఇలా చెప్పొచ్చు: కొన్ని ప్రాధమిక సూత్రాలతో, పునారావృత్తమయే పరిమితమైన గణనతో చేసేవని అర్థం. ఉదాహరణకి, హెచ్చవేతలని ఇలా వర్ణించవచ్చు:

x . 0 = 0

x . Sy = x .y + x ; దీని అర్థం – x times successor of y equals x times y plus x

ఉదాహరణకి, 7 X 3 విలువని ఎలా కనుక్కుంటామో చూడండి: 7 . 3 = 7 . S2 = 7 . 2 + 7 = 7 . S1 + 7 = (7 . 1 + 7) + 7 = (7 . S0) + 7 + 7 = (7 .0) + 7 + 7 + 7 = 0 + 7 + 7 + 7 = 21. పైన ఉన్న రెండో ఫార్ములాని పదేపదే వాడి చివరకి, విలువని సాధించాం. గూడెల్ కనుగొన్న గొప్ప విషయం, కూడికలు, హెచ్చవేతలు, ప్రధాన సంఖ్యలు మొదలైన వాటిని గురించిన IAలో గల సంఖ్యాసూత్ర సత్యాలకన్నిటికీ సమతుల్యమైన ఫార్ములాలని FA భాషలో రాబట్టగలమని చూపెట్టాడు. అది ఎలా చేశాడో ఇక్కడ వివరించడం సాధ్యం కాదు కాని, గుర్తించవలసిందేమిటంటే, IAకీ FAకీ అవినాభావ సంబంధం ఉంది.

దీనిని కాస్త జాగ్రత్తగా పరిశీలిద్దాం. కొన్ని సంకేతాలతో ఫార్ములాలతో మొదలెట్టి వాటినుండి కొత్త ఫార్ములాలని సృష్టించే నిర్ణితమైన పరిమిత సూత్రాలతో FA భాషని నిర్వచించాం. FA భాష వాస్తవానికి మారుస్తున్నది పదబంధాలని ఒక రూపం నుండి మరో రూపానికి. కాని IA భాష అయిన సంఖ్యా గణితంలోని కొన్ని సిద్ధాంతాలకీ FA భాషలోని ఆ రూపాలకీ గూడెల్ సమన్వయం చూపించాడు.

గణితంలో సారూప్యం (Mapping in Mathematics): గణిత శాస్త్రాలలో ఒక భాగం నుండి మరో భాగానికి అన్వయం చూపించి సమస్యలని సాధించడం సర్వసాధారణం. బీజగణితాన్ని రేఖాగణితానికి అన్వయించి వికాస యుగంలో యూరప్ విజ్ఞానశాస్త్రాలలో గొప్ప ప్రగతి సాధించిందని తెలుసు. ఉదాహరణకి రేఖాగణితంలో బిందువుని, (x, y) నిరూపకాలు (coordinates)గా, సరళరేఖని ఓ సమీకరణం (equation)గా, వృత్తాన్ని మరో రకం సమీకరణంగా అభివర్ణించి లెక్కలు చెయ్యడం చాలా సులువు. రెండు రేఖలు ఎక్కడ కలుసుకుంటాయి అని అడిగితే, x, y, లతో రెండూ సమీకరణాలు వేసి ఠకీమని చెప్పవచ్చు.

గూడెల్ సంఖ్యలు

MA భాషలో FA లోని ఫార్ములాల ఆకృతి గురించి చెప్పే విషయాలని, సంఖ్యాపరంగా అన్వయించి చెప్పవచ్చని చూపెట్టడం గూడెల్ అద్భుత మేధకో తార్కాణం. FA లోని ఫార్ములాలని సంఖ్యలతో అన్వయించి ప్రతి సంకేతానికీ ఈ క్రింది పట్టికలో ప్రకారం ఓ సంఖ్యనిచ్చాడు:

పట్టిక 2. గూడెల్ సంఖ్యలు

సంకేతం	గూడెల్ సంఖ్య
~	1
∨	2
⊃	3
∃	4
∀	5
0	6
S	7
(	8
)	9
=	10
+	11
.	12

ఇలా ప్రతి సంకేతానికీ ఓ సంఖ్యని నిర్దేశించి, అనేక సంకేతాలున్న ఫార్ములాకి సంఖ్య కనుక్కోడానికి ఓ మార్గం చెప్పాడు: ఆ ఫార్ములాలోని ప్రతి సంకేతానికీ, దాని స్థానానికి సంబంధించిన ప్రధాన సంఖ్యని ఆ సంకేతపు గూడెల్ సంఖ్యని ఘాతాంశంగా తీసుకోవాలి. ఆ విధంగా ప్రతి సంకేతానికీ వచ్చే విలువని హెచ్చిస్తే ఫార్ములాకి కావలసిన సంఖ్య వస్తుంది. ఇది తెలుగులో చెప్పడానికి కాస్త గజిబిజిగా ఉంది కాని ఓ ఉదాహరణతో సులభంగా అర్థమవుతుంది.

ప్రధాన సంఖ్యలు ఈ వరుసలో, 2, 3, 5, 7, 11, 13, 17, …., అనంతంగా ఉన్నాయని గుర్తు తెచ్చుకోండి. ‘0 = 0’ అన్న ఫార్ములాని తీసుకుందాం. ఈ ఫార్ములాలో మూడు సంకేతాలున్నాయి – సున్నా, సమానపు గుర్తు, సున్నా. మొదటి మూడు ప్రధాన సంఖ్యలు, 2, 3, 5. ఫార్ములా లోని మూడు సంకేతాలకీ (సున్నా, సమానం, సున్నా) పై పట్టిక నుండి వరుసగా గూడెల్ సంఖ్యలు: 6, 10, 6. ఆఫార్ములాకి గూడెల్ సంఖ్య: 2⁶ x 3¹⁰ x 5⁶ = 59, 049, 000, 000. ఇంత చిన్న ఫార్ములాకి అంత పెద్ద సంఖ్యా అని ఆశ్చర్యపోకండి. ఆ సంఖ్యని కనుక్కునే విధానం సులభంగానూ, నిర్దుష్టంగానూ ఉందని మాత్రం గ్రహించండి.

మరో ఫార్ములా, ~(S0 = SS0). దీని గూడెల్ సంఖ్యని కనుక్కోడానికి, ఫార్ములా లోని తొమ్మిది సంకేతాలకి సరిపడా, మొదటి తొమ్మిది ప్రధాన సంఖ్యలని – 2, 3, 5, 7, 11, 13, 17, 19, 23 – తీసుకొని, ఆ సంకేతాల గూడెల్ సంఖ్యలు – 1, 8, 7, 6, 10, 7, 7, 6, 9 – తో ఇలా హెచ్చించాలి: 2¹ x 3 ⁸ x 5 ⁷ x 7⁶ x 11¹⁰ x 13⁷ x 17⁷ x 19⁶ x 23⁹. ఇది మనం ఊహించలేనంత పెద్ద సంఖ్య. కానీ ఆ విషయం మనకనవసరం. ఏ ఫార్ములా ఇచ్చినా దానికి సరిపడా గూడెల్ సంఖ్య కనుక్కోగల మన్నదే ముఖ్యం. మరో విషయం. గూడెల్ సంఖ్య ఇస్తే దాని నుండి ఫార్ములాని రాబట్టగలం కూడాను!

ఓ సిద్ధాంతం నిరూపించడానికి మొదట ఓ ఫార్ములాతో మొదలెట్టి మెట్లు మెట్లుగా క్రమబద్ధమైన సూత్రాలని పాటిస్తూ ఫార్ములాలని మార్చి చివరకి రావలసిన సిద్ధాంతాన్ని రాబడతాము. ఆ క్రమ వరుసలో వున్న ఫార్ములాలని కలిపితే అది ఆ వరుసలోని చివరి ఫార్ములాకి నిరూపణ. ప్రతి ఫార్ములాకి గూడెల్ సంఖ్య ఎలా కనుక్కోవచ్చో పైన తెలుసుకున్నాం. f1, f2, f3, … ఇవి వరుసగా ఆయా ఫార్ములాల గూడెల్ సంఖ్యలని సూచిస్తే, వాటినన్నిటినీ ఈ విధంగా వరుసగా ఉన్న ప్రధాన సంఖ్యలకి ఘాతాంశాలుగా రాసి హెచ్చిస్తే వచ్చే సంఖ్య – 2^f1 X 3^f2 X 5^f3 x 7^f4 X … – దానిని ఆ ఫార్ములా వరుస (నిరూపణ) గూడెల్ సంఖ్య అంటాం.

ఒక్కసారి అవలోకన చేసుకుందాం: FA లోని ప్రతి సంకేతానికీ ఓ గూడెల్ సంఖ్య ఇచ్చాం. ఓ ఫార్ములాలో ఉన్న సంకేతాలు, వాటి స్థానాలని బట్టి, ప్రధాన సంఖ్యల ఆధారంగా, ఫార్ములాకి సంఖ్య కనుక్కోగలం. అలాగే ఫార్ములాల వరుసకి గూడెల్ సంఖ్యని కనుక్కోగలం. గూడెల్ సంఖ్యలలో ఉన్న ఓ ముఖ్యమైన గుణం – గూడెల్ సంఖ్యని తీసుకొని అది ఏ ఫార్ములాలని, వాటిల్లో ఏ వరుసలో ఏ సంకేతాలు ఏ స్థానంలో వస్తాయో ఖచ్చితంగా తెలుసుకోవచ్చు!

సంఖ్యాపరమైన అధిగణితం (Arithmetization of Meta-Mathematics)

FA సంకేతాల భాష. సంకేతాల సముదాయాన్ని ఒక రూపం నుండి మరో రూపానికి కొన్ని క్రమబద్ధమైన సూత్రాల ద్వారా ఎలా మార్చవచ్చో పైన తెలుసుకున్నాం. FA లోని ఫార్ములాల గురించి, మనం MA భాషలో మాట్లాడుకోవచ్చు. తెలుగు నేర్చుకునే ఇంగ్లీషు వాళ్ళ ‘The word అమ్మ means mother’ అన్న వాక్యం తెలుగు గురించి ఇంగ్లీషు లోని వాక్యం. అలాగే FA లోని పదబంధం ‘~(౦ = ౦)’ గురించి “~ is the first character of ‘~(౦ = ౦)’” అని MA భాషలో చెప్పవచ్చు. అదే వాక్యాన్ని సంఖ్యాపరంగా గూడెల్ సంఖ్యల ద్వారా కూడా చెప్పవచ్చు.

పై ఫార్ములాకి పైన చెప్పిన విధంగా గాడెల్ సంఖ్య (2¹ X 3⁸ X 5⁶ X 7¹⁰ X 11⁶ X 13⁹) కనుక్కుందాం. అది చాలా పెద్ద సంఖ్య అని తెలుస్తోంది కదా. దానిని a అందాం. a లోని మొదటి ప్రధాన సంఖ్య ఘాతాంశం ఎంత? 1. అంటే, “a లో 2 ఒక కారణాంకం; 22 కారణాంకం కాదు”. ఇది సంఖ్యాపరమైన వాక్యం. మన ఫార్ములాలో మొదటి సంకేతం ఫలానా అనేదానిని ఓ సంఖ్యాపరమైన వాక్యం ద్వారా చెప్పగలిగాం – గూడెల్ సంఖ్యల మూలంగా!

అంతేకాదు, ఈ సంఖ్యాపరమైన వాక్యాన్ని FA భాషలో కూడా చెప్పవచ్చు:

(∃z) (SSS…SSS0 = z . SS0) ∧ (~∃z) (SSS…SSS0 = z . (SS0 . SS0))

దీనినిలా చదువుతారు: “zకి రెండింతలయితే aకి సమానమయేటట్లు z అనే సంఖ్య ఉన్నది; మరియు (∧ అంటే and అని అర్థం) zకి నాలుగింతలయితే aకి సమానమయేటట్లుగా ఏ z సంఖ్యా లేదు”. పైన SSS…SSS తో సూచించినది aకి సంఖ్యావాచకం – a విలువ ఎంతో అన్నిసార్లు S వస్తుంది అని ఆ సూచిక అర్థం.

పైన జరిగినదాన్ని జాగ్రత్తగా పరిశీలించండి. FA భాషలో ఉన్న ఫార్ములాల ఆకృతి గురించి MA భాషలో ఉన్న వాక్యాలని IA భాషలో కారణాంశాల (factorization) పరంగా మాట్లాడి, దానినే FA భాషలో రూపొందించాం! ఈ మూడు భాషల మధ్యగల సంబంధాన్ని ఇలా సూచించవచ్చు:

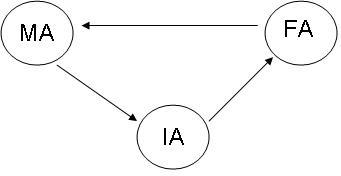
అంటే FA లో పదబంధాల గురించి FA లోనే, పరోక్షంగానయినా ఖండితంగా, మాట్లాడవచ్చన్నమాట. ఇది చాలా కీలకమైన విషయం. దీనిని ఇంకాస్త జటిలమైన వాటికి, ఫార్ములాల వరస (sequence of formulas) కి, అన్వయిద్దాం.

నిరూపించగలగడం (Provability in FA): FA లో ఏఫార్ములానైనా నిరూపించాలంటే స్వయంసిద్ధ సూత్రాలలోని ఒక ఫార్ములాతో మొదలెట్టి వరుసగా క్రమమైన సూత్రాలు వాడుతూ, కొత్త ఫార్ములాలని సృష్టిస్తూ చివరికి మనం నిరూపించదలచుకున్న ఫార్ములాని రాబట్టడం. “౦ = ౦” అన్న ఫార్ములాని ఎలా రాబట్టవచ్చో పైన చూశాం. (FA లో రాయగలిగే ప్రతి ఫార్ములాని ఇలా రాబట్టలేం. ఉదాహరణకి “~(0 = 0)” అన్న ఫార్ములాని రాబట్టగలరేమో ప్రయత్నించండి.) ఈ ఫార్ములాల వరుస గురించి MA లో ఇలా చెప్పవచ్చు: “ఈ ఫార్ములాల వరుస చివరి ఫార్ములాకి నిరూపణ”.

చివరి ఫార్ములా గూడెల్ సంఖ్య n అనుకుందాం. దాని నిరూపణ కొన్ని ఫార్ములాల వరుస అనీ, వాటినన్నిటినీ కలిపి ఓ గూడెల్ సంఖ్యని రాబట్టగలమనీ విశదమవుతుంది. ఆ సంఖ్యని m అందాం. ఈ రెండు సంఖ్యల మధ్య సంబంధాన్ని ఇలా చెప్పొచ్చు: “గూడెల్ సంఖ్య m గల ఫార్ములా వరుస, గూడెల్ సంఖ్య n గల ఫార్ములాకి నిరూపణ.” దీనిని IA భాషలో proves(x, y) అని సూచిద్దాం. ఇది ప్రాధమిక పునారావృత్త సంబంధమని గూడెల్ చూపెట్టాడు. ప్రాధమిక పునారావృత్తం అంటే: x, y అన్న ఏ రెండు సంఖ్యలు ఇచ్చినా, x గూడెల్ సంఖ్య అవునో కాదో తెలుసుకొని, అది సూచించే ఫార్ములాల వరుసని కనుక్కొని, ఆ వరుసలో చివరి ఫార్ములాకి గూడెల్ సంఖ్యని గణించి, అది సంఖ్య yకి సమానమో కాదో తేల్చి చెప్పవచ్చు.

ప్రాధమిక పునారావృత్త సంబంధం అంటే దీనికి కూడా FA భాషలో ఫార్ములా రూపం ఇవ్వవచ్చన్నమాట. దానినే PROVES(x, y) అని సూచిద్దాం. IA భాషలో proves అనీ, FA భాషలో PROVES అనీ రాశానని గమనించండి. ఇక్కడ PROVES అన్నది FA భాషలో అనేక గుర్తులబంధాన్ని క్లుప్తంగా సూచించే ఫార్ములా మాత్రమే.

స్వీయ ప్రతిక్షేపణ (Self-Substitution): FA లో స్వతంత్ర చలనరాశి (free variable) గల ఓ ఫార్ములాని తీసుకుందాం: ∃x (x = Sy) ఫార్ములాలో y అలాంటి చలనరాశి. దానికి మనం ఏ విలువనైనా ఇవ్వవచ్చు. ఈ ఫార్ములాకి గూడెల్ సంఖ్య ఉంటుంది కదా. దాని విలువ m అనుకుందాం. ఆ ఫార్ములాలో y బదులు m రాయవచ్చు – సంఖ్యావాచకంగా: ∃x (x = SSSSSSS….S0). ఇక్కడ అనేక సార్లు S ఉన్నది చూడండి. ఎన్నిసార్లంటే, m అన్నిసార్లు. అయితే ఈ కొత్త ఫార్ములా కూడా FA భాషలోనిదే. దీనికీ ఒక గూడెల్ సంఖ్య ఉంటుంది.

X గూడెల్ సంఖ్యగల ఫార్ములాలో y చలనరాశికి బదులు xని ప్రతిక్షేపిస్తే వచ్చే ఫార్ములా యొక్క గూడెల్ సంఖ్యని substitute(x, 17, x) అందాం. (y చలనరాశి గూడెల్ సంఖ్య 17). మరలా గూడెల్, సంఖ్యాగణితంలో substiture(x, 17, x) అన్నది ప్రాధమిక పునారావృత్తమైనదని చూపించాడు. అంటే దీనినే FA భాషలో కూడా సూచించగలం. దీనిని SUBSTITUTE(x, 17, x) గా సూచిద్దాం. మరోసారి, FA భాషలో ఇది అనేక సంకేతాల సముదాయమనీ, క్లుప్తంగా దానిని SUBSTITUTE(x, 17, x) గా పిలుస్తున్నామనీ గుర్తుంచుకుందాం. ఇది ఫార్ములా కాదు; ఇది ఓ సంఖ్యకి క్లుప్తంగా ఇచ్చే పేరు మాత్రమే.

గూడెల్ మొదటి అసంపూర్ణ సిద్ధాంతం

ఇప్పుడు గూడెల్ సిద్ధాంత నిరూపణ ఇవ్వడానికి కావలసిన సామగ్రి అంతా మన దగ్గర ఉంది. పైన PROVES(x, z) అన్న FA ఫార్ములా గురించి తెలుసుకున్నాం. దీనికి MA భాషలో అర్థం: “x గూడెల్ సంఖ్య గల ఫార్ములా వరుస, z గూడెల్ సంఖ్య గల ఫార్ములాకి నిరూపణ.” ఈ ఫార్ములా నుండి ఓ రూపాంతరీకరణ సూత్రం ద్వారా మరో ఫార్ములాని సృష్టిద్దాం: (∃x) PROVES(x, z). దీనికి MA భాషలో అర్థం: “z గూడెల్ సంఖ్య గల ఫార్ములాని నిరూపించే (x గూడెల్ సంఖ్య గల) ఫార్ములా వరుస ఉన్నది”. దానినే క్లుప్తంగా, “గూడెల్ సంఖ్య z గల ఫార్ములాని నిరూపించవచ్చు”. ఈ ఫార్ములాకి ముందర ~ పెడితే దానికి విరుద్ధమైన ఫార్ములా వస్తుంది: ~(∃x) PROVES(x, z). MA లో దాని అర్థం: “గూడెల్ సంఖ్య z గల ఫార్ములాని నిరూపించలేము”. ఇప్పుడు దీంట్లో z ని మార్చి, వేరే ఫార్ములా రాద్దాం:

~(∃ x) PROVES (x, SUBSTITUTE (y, 17, y))

దీని అర్థం: “గూడెల్ సంఖ్య substitute(y, 17, y) గల ఫార్ములాని నిరూపించలేము”. దీంట్లో y అన్న స్వేచ్ఛా చలనరాశి ఉన్నదని గమనించండి. చలనరాశి ఉన్నది కనుక ఈ ఫార్ములా అవునో కాదో చెప్పలేము. ఉదాహరణకి సంఖ్యాగణితంలో, x + 5 = 0, అన్నది నిజమో కాదో x విలువ బదులు పెడితే కాని చెప్పలేం. అలాగే పైన రాసిన FA ఫార్ములా లో y బదులు ఏదైనా విలువ ఇవ్వాలి. ఏ విలువ ఇద్దాం? ఆ ఫార్ములాకి మిగిలిన అన్ని ఫార్ములాల లాగే గూడెల్ సంఖ్య ఉంది. దానిని n అందాం. పై ఫార్ములాలో y కి బదులు n రాద్దాం.

~(∃ x) PROVES (x, SUBSTITUTE (n, 17, n))

(వాస్తవానికి పైన (n, 17, n) అని కాకుండా, (SSS…SSS0, SSS…SSS0, SSS…SSS0) అని S ని మొదట n సార్లు, తరువాత పదిహేడు సార్లు, ఆ తరువాత మళ్ళీ n సార్లు రాయాలి. కాని క్లుప్తంగా (n, 17, n) అని సంఖ్యావాచకాల రూపాలని వాడాము.)

ఈ ఫార్ములాని గూడెల్ పేరు మీద, G, అని పిలుస్తారు. దీనికి MA భాషలో అర్థం: “గూడెల్ సంఖ్య substitute(n, 17, n) గల ఫార్ములాని నిరూపించలేము.” ఇప్పుడు దీంట్లో చలనరాశు లేమీ లేవు కనుక ఇది నిజమో కాదో మనం చెప్పగలగాలి.

ఫార్ములా G కి గూడెల్ సంఖ్య ఉండాలి. దానిని g అని పిలుద్దాం. దాని విలువెంత? substitute(n, 17, n) అంటే గూడెల్ సంఖ్య n గల ఫార్ములాలో y కి బదులు n పతిక్షేపిస్తే వచ్చే ఫార్ములా యొక్క గూడెల్ సంఖ్య. మరి మనం G ఫార్ములాని రాబట్టిందే అలా ప్రతిక్షేపించే గదా. కాబట్టి g = substitute(n, 17, n).

ఇప్పుడు G కి MA భాషలో అర్థం: “ఫార్ములా G ని నిరూపించలేము”. అంటే మనం FA భాషలో సృష్టించిన ఓ ఫార్ములా తనను గురించి తానే చెప్తున్నది. ఏమని? తనని నిరూపించలేమని! అది నిజమా? కాదా?

G ని నిరూపించగలం అనుకుందాం. అంటే, FA లో స్వయంసిద్ధ సూత్రాలు మొదలుకొని క్రమబద్ధమైన నియమాలతో, ఓ ఫార్ములాల వరుస చివరకి ఫార్ములా G తో అంతమవాలి. ఈ ఫార్ములా వరుసకి గల గూడెల్ సంఖ్యని k అందాం. అంటే proves(k, substitute(n, 17, n)) అన్నది నిజం. దీనినే FA లో PROVES(k, SUBSTITUTE(n, 17, n)) అని రాస్తాం. దానినుంచే FA లో గల ఓ సూత్రం ద్వారా, (∃ x) PROVES (x, SUBSTITUTE (n, 17, n) అన్న ఫార్ములాని రాబట్టవచ్చు. కాని దీనికీ G కీ తేడా కేవలం ~ మాత్రమే. అంటే ఇది G కి విరుద్ధం – ~G. G ని నిరూపించగలం అనుకుంటే, ~G ని నిరూపించగలం!

ఏ వ్యవస్థలోనయినా పరస్పరం విరుద్దమైన రెండు ప్రతిపాదనలు నిజమైతే ఆ వ్యవస్థ వైరుధ్యాల పుట్ట. అలాంటి వ్యవస్థని పునాదిగా విజ్ఞానశాస్త్రాలు మనలేవు. గణితం అనేక విజ్ఞానశాస్త్రాలకి పునాది. గణితంలో కెల్లా ముఖ్యమైనది సంఖ్యా గణితం. దాంట్లో కూడికలూ, హెచ్చవేతలూ, ప్రధాన సంఖ్యలూ మౌలికమైన భావనలు. వాటినే FA భాష క్రమబద్ధం చేసింది. FA వైరుధ్యాల పుట్ట అంటే సంఖ్యా గణితమూ అంతే! అప్పుడు విజ్ఞానశాస్త్రాలకిక పునాదులుండవు!

మనం అంత దూరం వెళ్ళకుండా FA వైరుధ్య రహితం అనుకుందాం. అంటే G ని నిరూపించలేం. G తన గురించి తను అన్నది అదే కదా. అంటే FA లో ఉన్న ఓ సత్యాన్ని మనం నిరూపించలేము. ఇది హిల్బర్ట్ పథకానికి గొడ్డలిపెట్టు. ఇది గూడెల్ మొదటి అసంపూర్ణ సిద్ధాంతం: “FA వైరుధ్యరహితమైతే, అది అసంపూర్ణం”.

దీని పర్యవసానం ఇంతటితో ఆగలేదు. FA వైరుధ్య రహితం అని నిరూపించగలమా?

గూడెల్ రెండో సిద్ధాంతం

గూడెల్ మొదటి సిద్ధాంతాన్ని FA భాషలోనే ఓ ఫార్ములాగా రాయవచ్చు. “FA వైరుధ్య రహితం” అన్న దానిని A గా సూచిద్దాం. అప్పుడు FA లో ఆ ఫార్ములా: “A ⊃ G”. (MA భాషలో దీని అర్థం: “A implies G”.) దీనిని FA లో రుజువు చెయ్యగలం (అంటే స్వయంసిద్ధ ఫార్ములాలతో మొదలెట్టి, సూత్రాలతో “A ⊃ G” ని FA లో రాబట్టగలం.) ఫార్ములా A ని రాబట్టగలిగితే, G ని కూడా రాబడతాం. అంటే G ని నిరూపించగలుగుతాం. కాని G ని నిరూపించలేము అని పైన గూడెల్ మొదటి సిద్ధాంతం ద్వారా రుజువు చేశాం. కాబట్టి A ని కూడా నిరూపించలేము. అంటే “FA వైరుధ్యరహితం,” అన్నది నిరూపించడం అసాధ్యం!

ఈ నిరూపించడం అనేది మనం FA లోని సూత్రాలకు కట్టుబడి చేస్తున్నామని గుర్తుంచుకోవాలి. ఓ వ్యవస్థ ని వైరుధ్య రహితం అని ఆ వ్యవస్థలోని సూత్రాల ఆధారంగా చూపించలేము. మరో వ్యవస్థనాధారంగా చూపెట్టవచ్చు. కాని అప్పుడు ఆ మరో వ్యవస్థ వైరుధ్య రహితమని నిరూపించలేము.

ఇది హిల్బర్ట్ పథకానికి చావు దెబ్బ. మరోసారి హిల్బర్ట్ సమాధి మీద మాటలని గుర్తు తెచ్చుకుందాం: “తెలుసుకోగలం, తెలుసుకుంటాం”. గూడెల్ తెలుసుకోలేమని వాదించడం కాదు, శాస్త్రీయంగా నిరూపించాడు!

ముగింపు

గత శతాబ్దంలో భౌతిక శాస్త్రం అనూహ్యమైన మార్పులకి లోనయింది. సాపేక్ష సిద్ధాంతం ప్రకారం, రెండు సంఘటనలు ఒకే సమయంలో జరిగాయని ఒకరికనిపిస్తే, మరొకరికి అవి వేరు వేరు సమయాల్లో జరిగినట్లనిపించవచ్చు. అనిశ్చితత్వ నియమం (Uncertainty Principle) ప్రకారం, వస్తువు స్థానమూ, వేగమూ ఒకేసారి ఖచ్చితంగా కనుక్కోలేము. గణితంలో అనిశ్చితత్వ ముంటుందని ఎవరూ ఊహించలేదు. కాని గూడెల్ ఏ గణిత వ్యవస్థా సంపూర్ణమూ, వైరుధ్యరాహిత్యమూ అని నిరూపించడం అసాధ్యమని రుజువు చేశాడు. వైరుధ్యరహితమైతే ఆ వ్యవస్థ అసంపూర్ణమయి తీరుతుంది.

ఈ అసంపూర్ణ సిద్ధాంతాలకీ కంప్యూటర్లకీ సంబంధం ఏమిటి? గూడెల్ పేపరు ప్రచురితమయేనాటికి కంప్యూటర్లు లేవు; ఆ గణితవేత్తలెవరూ కంప్యూటర్ల గురించి ఆలోచించడం లేదు. Alan Turing అనే బ్రిటిష్ గణితవేత్త మాత్రం FA లాంటి క్రమబద్ధమైన వ్యవస్థలని (formal systems) సూక్ష్మంగా పరిశీలించి, వాటిలోని వివేచన కేవలం కొన్ని సంకేతాలని నియమబద్ధంగా మార్చడంతో సమానమనీ, అది యాంత్రికంగా చెయ్యవచ్చనీ భావించాడు. అలాంటి యంత్రాలని టూరింగ్ మెషీన్స్ అంటారు. అంటే ఇవి కొన్ని ఫార్ములాలతో మొదలెట్టి క్రమబద్ధమైన సూత్రాల ద్వారా కొత్త ఫార్ములాలని సృష్టిస్తాయి. ఈ యంత్రాలు కూడా సాధించలేని ఫార్ములాలు ఉన్నాయి అని టూరింగ్ చూపించాడు. ఆ విధంగా గూడెల్ సిద్ధాంతాలని మరో మార్గం ద్వారా టూరింగ్ రుజువు చేసి, హిల్బర్ట్ పథకం సాగదన్నాడు. ఆ టూరింగ్ యంత్రాల గురించీ అవి ఆధునిక కంప్యూటర్లకి ఎలా దారి తీసిందీ వచ్చే వ్యాసాలలో తెలుసుకుందాం.

నేనీ వ్యాసం రాయడానికి ఉపయోగించుకున్న గ్రంథాలు:

1. “Gödel’s Proof” by Ernest Nagel and James R. Newman. Edited and with a New Foreword by Douglas R. Hofstadter. New York University Press, 2001. గూడెల్ సిద్ధాంతాలని సామాన్యప్రజలకి మొట్ట మొదటగా పరిచయం చేసినది వీరే. ముందర 1956 లో Scientific American పత్రికలో వ్యాసం రాశారు. తర్వాత 1958 లో చిన్న పుస్తకంగా ప్రచురించారు. ఇది ప్రముఖ శాస్త్రవేత్తలెందరికో స్పూర్తినిచ్చిన పుస్తకం. అందరూ చదవదగ్గది. నా వ్యాసంలో గూడెల్ సిద్ధాంతాల నిరూపణకి ముఖ్య భాగాలు ఈ పుస్తకం నుండే తీసుకున్నాను. దీని 2001 ప్రచురణకి Hofstadter రాసిన ముందుమాట చాలా ఆసక్తికరమైనది. Hofstadter పధ్నాలుగేళ్ళ వయసులో్, వాళ్ళ నాన్నతో పుస్తకాల షాపుకెళ్ళినప్పుడు ఈ పుస్తకాన్ని చూసి ఉత్సాహపడి కొనుక్కున్నాడు. వాళ్ళ నాన్న, కొలంబియాలో Nagel క్రింద తనో ఫిలాసఫీ కోర్సు తీసుకున్నాననీ, స్నేహితులయ్యారనీ చెప్పాడు. అప్పుడే, Stanford సందర్శిస్తున్న Nagel ని పరిచయం చేసుకొని Hofstadter కుటుంబ మిత్రులయ్యారు.
2. “Gödel, Nagel, Minds and Machines,” Ernest Nagel lecture given at Columbia University by Solomon Feferman on September 27, 2007. Nagel and Newmanల పై పుస్తకాన్ని ప్రచురించడంలో Nagelకీ Gödelకీ మధ్య జరిగిన గొడవతో పాటు, యంత్రానికీ మనిషి మేధకీ, గణిత సిద్ధాంతాలని కనుక్కోవడంలో గల భేదాలూ, వాటి మీద గూడెల్ సిద్ధాంత ప్రభావం గురించీ చేసిన ప్రసంగం.
3. “Gödel, Escher, Bach: An Eternal Golden Braid,” by Douglas R. Hofstadter. Vintage Book Edition, May 1989. Copyright 1979 by Basic Books. Pulitzer బహుమతి నందుకున్న పుస్తకం. గూడెల్ పేరు సామాన్యప్రజలకి తెలియడానికి ఇదే కారణం. సంగీతం, చిత్రలేఖనంతో ముడిపెట్టి మనోరంజికంగా చేసిన ప్రయత్నం. గూడెల్ సిద్ధాంతాన్ని వివరించడానికి ఓ కొత్త Formalized Arithmetic భాష, Topographical Number Theory (TNT)ని, ప్రవేశపెట్టాడు. అభ్యాసానికి సమస్యలనీ, ఉదాహరణలనీ ఇచ్చి గూడెల్ నిరూపణ వంటబట్టడానికి చేసిన మంచి ప్రయత్నం.
4. “A Profile of Mathematical Logic” by Howard DeLong. Dover Publications, New York, 1970. అనాది కాలం నుండి, ఆధునిక కాలందాకా తర్కం ఎలా వృద్ధి చెందినదీ, చారిత్రక వివరాలతో, విషయం పలచబడకుండా చక్కగా వివరించి ఉత్కంఠతో చదివించే పుస్తకం. హైస్కూలు గణితం వచ్చిన వాళ్ళు కూడా చదివి చాలావరకు అర్థం చేసుకోవచ్చు. Nagel and Newman పుస్తకంతో పాటు తనకు స్ఫూర్తినిచ్చిన వాటిల్లో ఇదీ చాలా ముఖ్యమైనదని Hofstadter అన్నాడు.
5. “Logical Dilemmas: The Life and Work of Kurt Gödel” by John W. Dawson, Jr. A K Peters, 1997. గూడెల్ సంపూర్ణ రచనలని పోగుచేసినవారిలో రచయిత ఒకరు కనుక విషయం గురించి చక్కని అవగాహన కలవాడు. ఇది గూడెల్ సాధికారిక జీవితచరిత్ర.
6. “Gödel Upsets the Applecart” in “The Universal Computer: The Road from Leibniz to Turing” by Martin Davis. W. W. Norton and Company, 2000. నా వ్యాస పరంపరకి స్ఫూర్తిదాయకమైన పుస్తకం. గూడెల్ నిరూపణని ఈ అధ్యాయంలో పైపైన మాత్రమే వివరించాడు. కాస్త లోతుగా వెళ్ళాలంటే చివరి నోట్స్ చదవాలి.
7. “Incompleteness: The Proof and Paradox of Kurt Godel” by Rebecca Goldstein. WW Norton & Company, 2005. విస్మయపరచే గూడెల్ సిద్ధాంతాలనీ, అతని విపరీత మనస్తత్వాన్నీ కలపోసిన రచన.
8. “From Frege to Godel: A Sourcebook in Mathematical Logic, 1879-1931” by Jean van Heijenoort. Harvard University Press, 2002. తార్కిక గణితంలో ప్రఖ్యాత పేపర్లు, గూడెల్ పేపరుతో కలిసి, దీనిలో ఉన్నాయి. ఇది స్పెషలిస్టుల కోసమయినా, మూలరచనలకి రచయిత చేసిన పరిచయాలు సామాన్యపాఠకులకి ఆసక్తిని కలిగిస్తాయి.
9. “Fashionable Nonsense: Postmodern Intellectuals’ Abuse of Science” by Alan Sokal and Jean Brickmont. Picador, 1998. కొందరు సాహిత్య, సామాజికవేత్తలు, సైన్సు సిద్ధాంతాలని సరిగా అర్థం చేసుకోకుండా, ఏకరువు పెట్టి ప్రజలని తప్పుద్రోవ పట్టిస్తున్నారని దుయ్యబట్టిన పుస్తకం. పోస్ట్ మోడర్నిజం పేరిట Julia Kristeva, మరి కొందరు మేధావులు గూడెల్ సిద్ధాంతాలని అనవసరంగా ఉటంకించిన అనేకానేక వ్యర్థ రచనలని దీంట్లో తప్పుబట్టారు.
10. “Godel’s Theorem: An Incomplete Guide to Its Use and Abuse” by Torkel Franzén. A K Peters Ltd, 2005. గూడెల్ అసంపూర్ణ సిద్ధాంతాలకి శాస్త్రవేత్తలు కూడా తమకిష్టమొచ్చినట్లుగా అర్థాలు చెప్పి వక్రీకరిస్తున్నారని, వాటిని వివరించే పుస్తకం. ఇది సామాన్య పాఠకులకి అర్థం కావడం కష్టం.
11. “The IAS School of Mathematics” by Allyn Jackson. Notices of the AMS, Volume 49, Number 8, September 2002. సంస్థ స్థాపన మీదా, అప్పుడూ ఇప్పుడూ అక్కడ జరిగే పరిశోధనల గురించీ వ్యాసం.
12. “Science and Technology; Geniuses in Plato’s Sandbox” by Jonathan Weiner. NYT Book Review of WHO GOT EINSTEIN’S OFFICE? Eccentricity and Genius at the Institute for Advanced Study. By Ed Regis.