పరిచయము

    సచతుర్ముఖ షణ్ముఖ పంచముఖ ప్రముఖాఖిల దైవత మౌళిమణే …

అని సుప్రభాతము వినబడుతోంది. ఇందులో బ్రహ్మ చతుర్ముఖుడు, శివుడు పంచముఖుడు, కుమారస్వామి షణ్ముఖుడు. దైవములకు ఎక్కువగా ముఖాలుంటాయని మనము వింటూంటాము. అందుకే ప్రతిభావంతులను బహుముఖప్రజ్ఞాశాలురని చెబుతారు. దేవతలకు, రాక్షసులకు, ప్రాణులకు మాత్రమే ముఖాలు ఉంటాయనుకోకూడదు. ఘనస్వరూపాలకు కూడ ముఖములు (faces) లేక ఉపరితలములు ఉంటాయి. ఇట్టి ఘనస్వరూపాలలో మిక్కిలి ప్రసిద్ధి కెక్కినవి ప్లేటో ఘనస్వరూపాలు (Platonic solids). ఇవి ఐదు – చతుర్ముఖి (tetrahedron), ఘన చతురస్రము (cube), అష్టముఖి (octahedron), ద్వాదశముఖి (dodecahedron), వింశతిముఖి (icosahedron). గ్రీకు భాషలో హెడ్రన్ (hedron) అంటే పీఠము అని అర్థము. వీటికి ప్లేటో ఘనస్వరూపాలు అని పేరున్నా, ప్లేటోకు ముందే పైతాగోరస్‌కు ఇందులో కొన్నైనా (చతుర్ముఖి, ఘన చతురస్రము, ద్వాదశముఖి) తెలిసి ఉంటుందని ఊహ. తియేటెటస్ (Theaetetus) మిగిలిన రెంటిని (అష్టముఖి, వింశతిముఖి) కనుగొని యుండవచ్చు. ఏది ఏమైనా ఇప్పటికీ ఇవి ప్లేటో ఘనస్వరూపాలనే పిలువబడుచున్నాయి. ప్లేటో వీటికి పంచభూతముల గుణాలను ఆపాదించాడు – భూమి – ఘన చతురస్రము, గాలి – అష్టముఖి, నీరు – వింశతిముఖి, అగ్ని – చతుర్ముఖి, ఆకాశము – ద్వాదశముఖి. ఈ ఐదు ఘనస్వరూపాల శాస్త్రీయ గుణాలను కొద్దిగా తెలుసుకొందామా?

ఆయ్‌లర్ సిద్ధాంతము (Euler’s Theorem)

మొట్ట మొదట మనము కొన్ని సాంకేతిక పదాలతో పరిచయము చేసికోవాలి. ఇక్కడ మనము చూసే ఘనస్వరూపాలు సక్రమమైనవి (regular solids), అంటే వీటి అన్ని అంచుల (edges) నిడివి, అన్ని ముఖముల (faces) వైశాల్యము ఒక్కటే. ఇవి కాక వీటికి శీర్షములు (vertices) కూడ ఉంటాయి. శీర్షాలకు పరిమాణము లేదు (zero dimension), అంచుల పరిమాణము ఒకటి (one dimensional edges), ముఖాల పరిమాణము రెండు (two dimensional faces), ఘనస్వరూపపు పరిమితి మూడు (three dimensional solid). ఏ కుంభాకార (convex) ఘనస్వరూపానికైనా ఆయ్‌లర్ సిద్ధాంతము (Euler’s theorem) అన్వయిస్తుంది. ఈ సిద్ధాంతము ప్రకారము శీర్షముల సంఖ్య (V) + ముఖముల సంఖ్య (F) – అంచుల సంఖ్య (E) = 2.
కింది పట్టికలో ప్లేటో ఘనస్వరూపాలకు గల ఈ అంశముల వివరణ ఇవ్వబడినది.

పట్టిక 1: ఆయ్‌లర్ సిద్ధాంతము

ఘనస్వరూపము	శీర్షముల సంఖ్య(V)	అంచుల సంఖ్య(E)	ముఖముల సంఖ్య(V)	ముఖముల ఆకారము
చతుర్ముఖి (tetrahedron)	4	6	4	సమత్రిభుజము
ఘన చతురస్రము (cube)	8	12	6	చతురస్రము
అష్టముఖి (octahedron)	6	12	8	సమత్రిభుజము
ద్వాదశముఖి (dodecahedron)	20	30	12	సమపంచభుజము
వింశతిముఖి (icosahedron)	12	30	20	సమత్రిభుజము

(సమత్రిభుజము – equilateral triangle, సమచతురస్రము – square, సమపంచభుజము – regular pentagon)

అన్ని ఘనస్వరూపాలు ఆయ్‌లర్ సిద్ధాంతమునకు ఒడబడి యున్నవని మీరు సంతృప్తిపరచుకోవచ్చు. ఇంకొక విషయము ఈ పట్టికనుండి మీరు గ్రహించవచ్చు. అదేమంటే, చతుర్ముఖికి శీర్షాల సంఖ్య, ముఖాల సంఖ్య ఒక్కటే. కాని ఘన చతురస్రము, అష్టముఖి ఈ రెంటికి ఒకదాని శీర్షముల సంఖ్య మరొకదాని ముఖముల సంఖ్య. ఈ తారుమారు ద్వాదశముఖి, వింశతిముఖి ఈ రెంటికి కూడ వర్తిస్తుంది. గణితశాస్త్ర రీత్యా ఘన చతురస్రము, అష్టముఖి కవలలు (dual). అట్లే ద్వాదశముఖి, వింశతిముఖి కూడ కవలలే. చతుర్ముఖికి కవల మరొక చతుర్ముఖి (self dual). దీని అర్థమేమంటే, ఘన చతురస్రము ముఖాల కేంద్రాలను (face centres) కలిపితే మనకు అష్టముఖి లభిస్తుంది; అష్టముఖి ముఖాల కేంద్రాలను కలిపితే ఘన చతురస్రము లభిస్తుంది. దీనిని నిరూపించుటకై నేను పారదర్శకమైన ప్లాస్టిక్ రేకుతో (transparent plastic sheet) ఒక చతుర్ముఖిలో మరొక చతుర్ముఖిని (a tetrahedron in a tetrahedron – చిత్రము 1), ఒక అష్టముఖిలో ఘన చతురస్రముని (cube in an octahedron – చిత్రము 2), ద్వాదశముఖిలో ఒక వింశతిముఖిని నిర్మించాను (icosahedron in a dodecahedron – చిత్రము 4).

చతుర్ముఖి (tetraheron)

చిత్రము 1: ఒక చతుర్ముఖిలో మరొక చతుర్ముఖి (Tetrahedron in a tetrahedron)
చతుర్ముఖి అగ్రమును దాని ఎదురుగా ఉండే త్రిభుజపు కేంద్రమును కలిపితే మనకు త్రిరావృత్త అక్షము (120 డిగ్రీల భ్రమణము) లభిస్తుంది. నాలుగు త్రిభుజాల కేంద్రాలలో నాలుగు పిన్నులను గుచ్చాను. ఇవి త్రిరావృత్త అక్షాలను సూచిస్తాయి. కవల (చిన్న) చతుర్ముఖిలోని త్రిభుజము పెద్ద చతుర్ముఖి శీర్షానికి ఎదురుగా ఉంటుంది. దీనికి నాలుగు త్రిరావృత్త అక్షాలు (120 డిగ్రీల భ్రమణము), మూడు ద్విరావృత్త అక్షాలు (180 డిగ్రీల భ్రమణము) ఉంటాయి. ఈ ద్విరావృత్త అక్షాలు ఎదురు అంచుల మధ్యబిందువులను కలిపే సరళరేఖలు.

చతుర్ముఖికి నాలుగు ముఖాలు ఉంటాయి. దీని సామ్యరూపము లేక సౌష్ఠవమును (symmetry) గమనించితే నాలుగు ముఖాల కేంద్రాల గుండా నాలుగు త్రిరావృత్త అక్షములు లేక ఇరుసులు (three-fold axes) మనకు కనబడుతాయి. దీని అర్థము ఏమంటే ఈ అక్షముగుండా చూస్తూ మనము ఘనస్వరూపాన్ని 120, 240 డిగ్రీలు తిప్పితే దాని ఆకారము మారదు. అంచుల నడిమి బిందువు (middle point) ద్వారా ద్విరావృత్త అక్షము (నిజముగా ఇది చతురావృత్త అక్షముతో కూడిన విలోమ పరిక్రియ) కనబడుతుంది. బ్రహ్మదేవుడు చతుర్ముఖుడు, అంతేకాక సృష్టికర్త అని పురాణాలు చెబుతాయి. వాని ఆ తలలు నాలుగు దిక్కులా ఉండేటట్లు చిత్రిస్తారు. కాని ఆ నాలుగు ముఖాలు చతుర్ముఖి ముఖాలుగా ఎందుకు ఉండరాదు? ఈ తలంపు సరి అని నా భావన. ఎందుకంటే జీవించటానికి కావలసిన రసాయనాలు కర్బనముతో (carbon) కూడి యుంటాయి. చతుర్ముఖి కేంద్రము కర్బనపు అణువు అనుకొందాము. చతుర్ముఖి శీర్షాలగుండా నాలుగు సంయోజక బంధాలు (valence bonds) వెళ్ళుతాయి. వజ్రానికిగల ఇట్టి బంధాలే దానికి కాఠిన్యాన్ని ఇస్తుంది. సిలికాన్‌లో (silicon) కూడ ఇట్టి బంధాలు ఉన్నాయి. ఈ బంధాల చివర నాలుగు భిన్నమైన రసాయనవర్గాలు ఉంటే, కేంద్రములో నున్న కర్బనమును సౌష్ఠవరహిత కర్బనపు అణువు అంటారు (asymmetric carbon atom). ఇట్టి అమరిక రసాయనమునకు ఒక సవ్యాపసవ్య గుణాన్ని ఇస్తుంది (chirality). ఒక దానికి మరొక దానికి దర్పణ సాదృశ్యము ఉంటుంది. దీనిని ఈ కింది రెండవ చిత్రములో చూడగలరు.

చిత్రము 2: సవ్యాపసవ్య గుణములతో బింబ-ప్రతిబింబాలు (Stereoisomers)
చతుర్ముఖి కేంద్రములో కర్బనపు అణువు ఉన్నదనుకొందాము. నాలుగు రంగుల పుల్లలు నాలుగు అణుబంధాలను సూచిస్తాయి. చివర నాలుగు విభిన్నమైన అణువులో లేక అణుసమూహాలో ఉంటాయి. చతుర్ముఖికి గల ఏ సౌష్ఠవ ప్రక్రియ (ద్విరావృత్త, త్రిరావృత్త అక్షములు మున్నగునవి) కూడ బింబ ప్రతిబింబాలను ఒకటి చేయజాలదు. ఇట్టి రసాయన సమ్మేళనమునకు సవ్యాపసవ్య గుణము ఉన్నది.

మాంసకృత్తులలో (proteins) ఒక విధమైన అమినోఆంలములు ఉపయోగించబడుతాయి (L-aminoacids), అలాగే డీ.ఎన్.ఏ.లో మరొక విధమైన పంచదారలు (D-sugars) ఉన్నాయి. వీటి సవ్యాపసవ్య గుణాన్ని తారుమారు చేస్తే భూమిపై జీవము (life) ఉండదు. గార్డ్‌నర్ (Martin Gardner) మహాశయుడు ఈ విషయాన్ని తన పుస్తకాలలో వినోదకరముగా వివరించియున్నాడు. మనము వాడే కొన్ని మందులలో కూడ ఒక విధమైన సవ్యాపసవ్య గుణము ఉంటుంది. ఒకటే పని చేస్తుంది, రెండవది జడముగా ఉంటుంది. కాని ఒక్కొక్కప్పుడు ఇది జడముగా నుండక అవాంఛనీయమైన ఫలితాలను కలిగిస్తుంది. 1960 దశకములో గర్భవతులకు వాంతులు కలగకుండ ఉండుటకై తాలిడోమైడ్ అనే మందును ఇచ్చేవారు. అందులో సవ్యపు, అపసవ్యపు గుణములు కలిగిన రెండు రసాయనాలు ఉన్నాయి. ఒకటి మాత్రమే సరిగా పని చెయ్యాలి, అంటే వాంతులను తగ్గించాలి, రెండవది ఎట్టి ప్రభావాన్ని శరీరములో కలిగించరాదు. కాని అది శిశువులను అంగవిహీనములుగా చేశాయి. కాబట్టి సవ్యాపసవ్య గుణము చాల ముఖ్యమైనది. పాస్తర్ (Pasteur), ఫిషర్ (Fisher), బైఫుట్ (Bijvoet), రామశేషన్ (Ramaseshan), ప్రెలోగ్ (Prelog) వంటి గొప్ప శాస్త్రజ్ఞులు ఈ క్షేత్రములో మహత్తరమైన వైజ్ఞానిక సంశోధనలను చేసియున్నారు. చతుర్ముఖికి చాల ముఖ్యమైన స్థానము రసాయన శాస్త్రములో ఉంది కాబట్టే ఈ చతుర్ముఖి ఆంగ్లనామముతో టెట్రాహెడ్రన్ (Tetrahedron) అనే విజ్ఞాన పత్రిక (science magazine) కూడ ఉంది.

ఘన చతురస్రము (cube), అష్టముఖి (octahedron)

చిత్రము 3: అష్టముఖిలో ఘన చతురస్రము (Cube in an octahedron)
మీరు త్రిరావృత్త (120 డిగ్రీల భ్రమణము) అక్షముగుండా చూస్తున్నారు. అష్టముఖికి ఉన్న ఎనిమిది సమభుజ త్రిభుజాకారములో ఉండే ఉపరితలాల కేంద్రములలో పిన్నులను గుచ్చి ఉన్నాను. నాలుగేసి పిన్నులున్న బిందువులను కలిపితే ఘనచతురస్రము యొక్క ఉపరితలమైన చదరమును చూడ వీలవుతుంది. పై త్రిభుజము ఎక్కువ ఎత్తులో ఉంది. మూడు వైపులా వేళ్ళాడే మూడు త్రిభుజాలు దీనికి కింద ఉంటాయి. అన్నిటికన్న కింద ఉన్న త్రిభుజపు కేంద్రములో ఉన్న పిన్ను మొనను చూడగలరు. దానినుండి పైకి లేచే మూడు త్రిభుజాల మధ్య ఉండే పిన్నుల మొనలను కూడ చూడవచ్చు. సమచతురస్రముల కేంద్రముల ద్వారా చతురావృత్త అక్షము (90 డిగ్రీల భ్రమణము) పోతుంది. త్రిభుజాల అంచుల మధ్యబిందువు ద్వారా ద్విరావృత్త అక్షము (180 డిగ్రీల భ్రమణము) పోతుంది. ఆ యా ఇరుసులతో ఆ యా డిగ్రీల భ్రమణమును కొనసాగిస్తే ఘనాకారములలో మార్పు ఉండదు. అది సామ్యరూపము లేక సౌష్ఠవము యొక్క సారాంశము.

ఈ రెండు ఘనస్వరూపాలు కవలలు గనుక, వీటిని ఒకే మారు పరిశీలిద్దాము. ఘన చతురస్రము చాల ప్రసిద్ధమైన ఘనస్వరూపము. ఘనపరిమాణమునకు కొలమానము ఘనమే! దీని ఆరు ఉపరితలాలు చదరాకారములో ఉంటాయి. ఎదురుగా ఉండే ఉపరితలాల కేంద్రాలను కలిపితే మనకు వచ్చే మూడు అక్షాల సౌష్ఠవము చతురావృత్తము. అంటే ఈ అక్షము గుండా 90 డిగ్రీలు తిప్పితే ఘనాకారపు స్వరూపము మారదు. ఇలా మూడు చతురావృత్త అక్షాలు (four-fold axes) ఉన్నాయి. ఘనాకారానికి నాలుగు వికర్ణాలు (body diagonals) ఉన్నాయి. ఈ రేఖల గుండా 120 డిగ్రీలు తిప్పితే ఘనాకారము మారదు. అనగా ఘానాకారానికి నాలుగు త్రిరావృత్త అక్షాలు (three-fold axes) ఉన్నాయి. ఎదురుగా ఉండే అంచుల మధ్యబిందువులను కలిపే రేఖలు ఆరు ఉన్నాయి. వీటి గుండా 180 డిగ్రీలు తిప్పితే ఘనాకారములో మార్పు ఉండదు. ఇవి ద్విరావృత్త అక్షాలు (two-fold axes). అష్టముఖికి కూడ మూడు చతురావృత్త, నాలుగు త్రిరావృత్త, ఆరు ద్విరావృత్త అక్షాలు ఉన్నాయి. ఇవిగాక వీటికి దర్పణా సాదృశ్యము కూడ ఉన్నది. వీటిని మూడవ చిత్రములో చూడగలరు. అష్టముఖి రసాయన శాస్త్రజ్ఞులకు పరిచితమైన ఘనస్వరూపము. ధన విద్యుచ్ఛక్తి కలిగిన కొన్ని లోహపు అణువుల (cation) చుట్టు ఉండే ఋణవిద్యుచ్ఛక్తి గలిగిన అణువులు (anion)ఈ అష్టముఖి స్వరూపములో అమర్చబడి ఉంటుంది. ఉదాహరణకు, సామాన్యమైన ఉప్పును (sodium chloride) తీసికొంటే, ఇందులో సోడియం లోహపు అణువుల చుట్టు ఆరు క్లోరైడు అయానులు ఉంటాయి. ఈ అమరికను మీరు ఇక్కడ చూడగలరు –

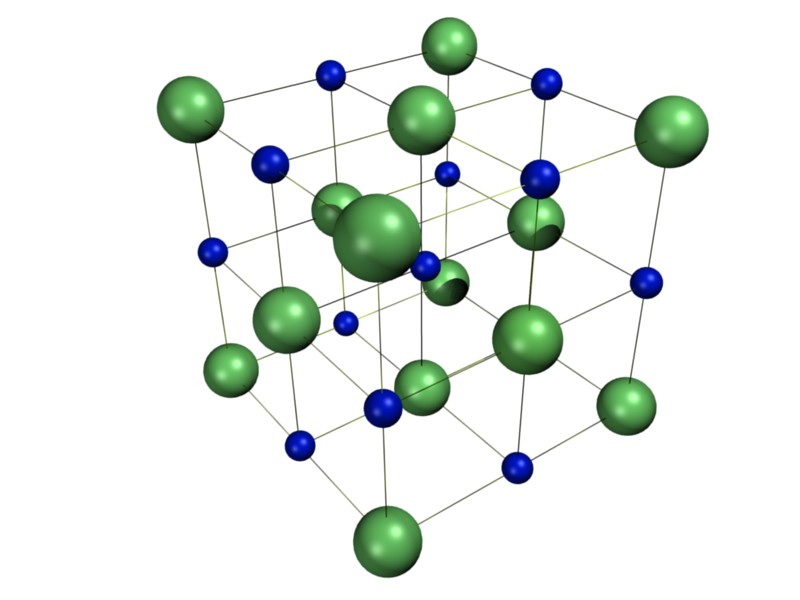
అష్టముఖి రూపములో కొన్ని ఖనిజాలు కూడ స్ఫటికీకరిస్తాయి. ఈ ఆకారములో ఉన్న రంగురంగుల ఫ్లోరైటు (Fluorite – Calcium Fluoride) ఖనిజాలను క్రింది చిత్రములో చూడగలరు –

ఘన చతురస్రము ఆకారములో ఒక రసాయనము కూడ ఉంది, దాని పేరు క్యూబేన్ (cubane – C₁₂H₁₂). ఘన చతురస్రముకి గల 12 అంచులు క్యూబేన్ కర్బన-కర్బన బంధాలు (carbon-carbon bonds). ఈ మాలిక్యూలును కింద చూడగలరు –

ద్వాదశముఖి (dodecahedron), వింశతిముఖి (icosahedron)

చిత్రము 4: ద్వాదశముఖిలో వింశతిముఖి (Icosahedron in a dodecahedron)
ద్వాదశముఖి పంచభుజముల కేంద్రములు, అందులోని వింశతిముఖి శీర్షములు ఒక్కటే. పంచావృత్త అక్షము ఎదురుగా ఉండే ఈ కేంద్రాలను కలుపుతుంది. మూడు పంచభుజములు కలిసే బిందువుగుండా త్రిరావృత్త అక్షము పోతుంది. ఎదురుగా ఉండే అంచుల మధ్యబిందువుల ద్వారా ద్విరావృత్త అక్షము ఉన్నది. మొత్తము 6 పంచావృత్త అక్షాలు (144 డిగ్రీల భ్రమణము), 10 త్రిరావృత్త అక్షాలు (120 డిగ్రీల భ్రమణము), 15 ద్విరావృత్త అక్షాలు (180 డిగ్రీల భ్రమణము) ఉన్నాయి ఈ రెండు ఘనస్వరూపాలలో.

మొదట సమబాహుత్రిభుజాలను (equilateral triangles) ఎన్నుకొందాము. మూడింటిని పక్క పక్కన అతికించితే మనకు పీఠము లేని చతుర్ముఖి వస్తుంది (చిత్రము 1), నాల్గింటిని అతికిస్తే అష్టముఖియొక్క అర్ధస్వరూపము లభిస్తుంది (చిత్రము 3), ఐదింటిని అతికిస్తే మనకు వింశతిముఖి కిరీటము (చిత్రము 4) దొరుకుతుంది. ఐదింటికన్న త్రిభుజాలను అతికించడానికి వీలు కాదు. ఆరు త్రిభుజాలతో ఘనస్వరూపము దొరకదు. ఆరు సమబాహు త్రిభుజాలు పక్క పక్కన ఉంటే అవి సమతలములో ఉంటాయి. ఆరు త్రిభుజాలను స్తూపముపై రిబ్బనులా చుట్టవచ్చు, కాని దీనిని ఒక కుంభాకార స్వరూపముగా చేయాలంటే ఐదు సమత్రిభుజాలు ఉండాలి. పంచావృత్త అక్షాలు లేక ఇట్టి ఘనస్వరూపాలను నిర్మించలేము. ఈ సిద్ధాంతాన్ని కూడ మొట్ట మొదట ఆయిలర్ కనుగొన్నాడు. ఈ ఘనస్వరూపాల ఆకారములో గుమ్మటమువంటి శిఖరాలను మనము చూస్తూనే ఉన్నాము. వీటిని ఆంగ్లములో geodesic domes అంటారు. ఇట్టి డోములను క్రీడారంగముల నిర్మాణములో మనము చూడగలము. దీనికి మూలపురుషుడు బక్‌మిన్స్టర్ ఫుల్లర్ (Buckminster Fuller). ఈ నిర్మాణములో బరువుతో బాటు సంపూర్ణత్వము ఉన్నది. అందుకే దీనిని టెన్సెగ్రిటీ (tensegrity – tensile integrity) అంటారు. ఇప్పుడు ఈ ఆకారములో ఇళ్ళను కూడ నిర్మిస్తున్నారు. వాల్ట్ డిస్నీ ఎప్కాట్ డోం చాల ప్రసిద్ధమైనది. దానిని ఇక్కడ చూడగలరు –

ద్వాదశముఖి, వింశతిముఖి, వీటిలో మనకు ఒక కొత్త సౌష్ఠవము కనబడుతుంది, అది పంచావృత్త అక్షముతో ఉండే సౌష్ఠవము. ద్వాదశముఖిలో 12 సమబాహు పంచభుజములు (regular pentagon) ఉన్నాయి. ఈ పంచభుజానికి అదే ఆకారములో ఉండే చిన్న భూషయ్యగారి పంచభుజికి ఏ సంబంధము లేదని మీతో మనవి చేస్తున్నాను! పంచభుజములో ఒక ప్రత్యేకత ఉన్నది. పంచభుజములోని ఐదు వికర్ణాలను కలిపితే మనకు మరొక చిన్న పంచభుజము లభిస్తుంది. అంతే కాక ఒక నక్షత్రాన్ని కూడ చూడ వచ్చును (చిత్రము 5).

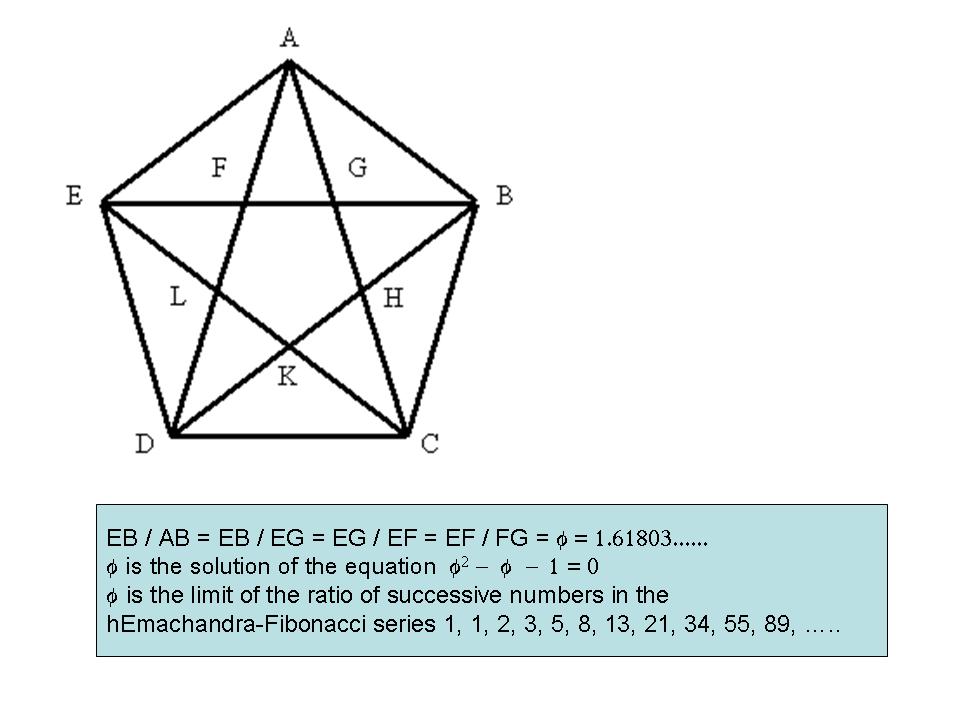
చిత్రము 5: సమభుజ పంచభుజము (Regular pentagon), అందులోని కొన్ని విచిత్రాలు

ఈ సమబాహు పంచభుజములో స్వర్ణనిష్పత్తి (golden ratio), దాని ద్వారా హేమచంద్ర-ఫిబొనాచ్చి (Hemachandra-Fibonacci numbers) సంఖ్యలు అంతర్గతమై ఉన్నాయి. ఈ స్వర్ణ నిష్పత్తి, హేమచంద్ర-ఫిబనాచ్చి సంఖ్యలు ఎన్నో రంగాలలో పదే పదే దర్శనమును ఇస్తాయి. శిల్పములలో, పూలలో, పండ్లలో, సంగీతములో, అలలలో, సర్పిలములో (spiral), ఛందస్సులో, ఇలా ఎన్నో రంగాలలో ఇవి గోచరిస్తాయి. ప్లేటో ఘనస్వరూపాలలో వింశతిముఖి గోళాకారమునకు (sphere) చాల దగ్గరిది. అందుకేనేమో ప్లేటో దీనికి గోళాకారపు బిందువుల రూపములో నున్న నీటి గుణమును ఆపాదించాడు. ద్వాదశముఖి రూపములో క్యూబేన్‌లా ఒక రసాయనము ఉంది, దాని పేరు డోడెకాహెడ్రేన్. దీని అమరికను కనుగొన్నవారిలో నా సహాధ్యాయి ఉష కూడ ఒకతె అన్నది నాకు గర్వ కారణము.

కర్బనపు సామాన్య స్ఫటిక రూపాలు – వజ్రము (diamond), బొగ్గు (graphite). 1980వ దశకములో కర్బనపు మరొక కొత్త రూపాన్ని కనుగొన్నారు. ఇందులో ఒక వింశతిముఖి రూపములో అమర్చబడిన 60 కర్బనపు అణువులు ఉన్నాయి (C₆₀). పైన ఉదహరించబడిన బక్‌మిన్స్టర్ ఫుల్లర్ గౌరవార్థము దీనిని ఫుల్లరీన్ (Fullerene) అంటారు. దీనికై క్రోటో, కర్లీ, స్మాలీలకు (Kroto, Curl, and Smalley) నోబెల్ బహుమతిని 1996లో ఇచ్చారు.

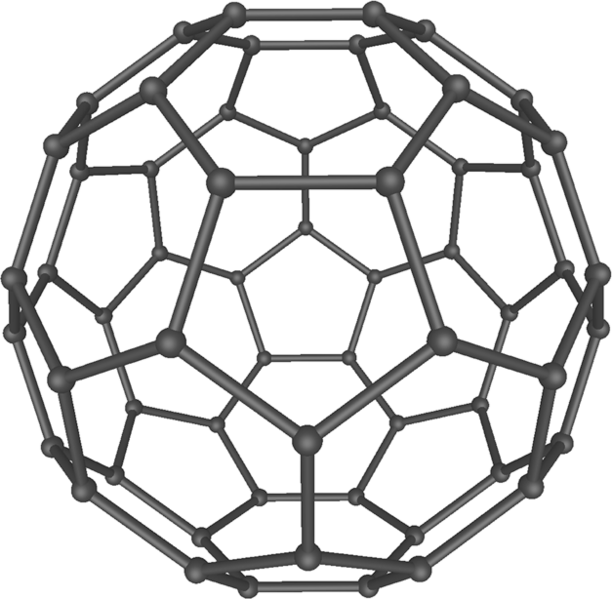
60 కర్బనపు అణువుల అమరిక

540 కర్బనపు అణువుల అమరిక

ఈ ఆకారాలను జబ్బు నిచ్చే కొన్ని సూక్ష్మజీవుల (viruses) అమరికలో కూడ చూడగలము. చెట్టులకు, పూలకు వ్యాధిని కలిగించే కొన్ని సూక్ష్మజీవులు, జలుబు, పోలియో మున్నగు వ్యాధులను కలిగించే వైరసులలోని మాంసకృత్తుల (proteins) అమరిక ఈ వింశతిముఖి రూపములో ఉంటుంది. ఒకప్పుడు ఈ రంగములో నేను కూడ కొద్దిగా పరిశోధన చేసియున్నాను. జలుబు నిచ్చే ఒక వైరసు అమరిక ఇక్కడ చూడగలరు.

నూతన సంవత్సర శుభాకాంక్షలు

ఈ ఐదు ప్లేటో ఘనస్వరూపాల ఆకారాలను శాస్త్రములో, యాంత్రిక విజ్ఞానములో, భవన నిర్మాణములో, చివరకు తినుబండారాలలో కూడ చూడ గలిగాము. నూతన సంవత్సరము ఆరంభమవ బోతుంది. ఇంతవరకు ఈ వ్యాసాన్ని మీరు చదివారంటే మీకు ఒక బహుమతిని ఇవ్వాలి. ద్వాదశముఖికి 12 ఉపరితలాలు ఉన్నాయి. ఆ 12 ఉపరితలాలపై సంవత్సరములోని 12 నెలల వారములను, తేదులను తెలిపే క్రీస్తు శకము 2008 సంవత్సరపు కాలెండర్‌ను మీకు అందజేస్తున్నాను. ఇందులో జనవరినుండి మే నెల వరకు గల ఆరు నెలల క్యాలెండర్‌ను ఆరు కలువబడిన పంచభుజములలో, అదే విధముగా జూన్ నెల నుండి డిశంబర్ నెలవరకు గల క్యాలెండర్‌ను ఆరు కలువబడిన పంచభుజాలలో ఇచ్చినాను. వాటిని పంచభుజములుగ కత్తిరించి ఒక దాని కొకటి చేరిస్తే రెండు బుట్టలు మీకు దొరుకుతాయి. వాటి రెంటిని చేరిస్తే 12 నెలల మొత్తము క్యాలెండర్ (చిత్రము 6) దొరుకుతుంది. మీ బల్లపై దానిని ఉంచుకొని ఆనందించండి!

చిత్రము 6-1: జనవరినుండి జూన్‌వరకు పంచభుజములలో నెలల పట్టిక

చిత్రము 6-2: జులైనుండి డిశంబర్‌వరకు పంచభుజములలో నెలల పట్టిక

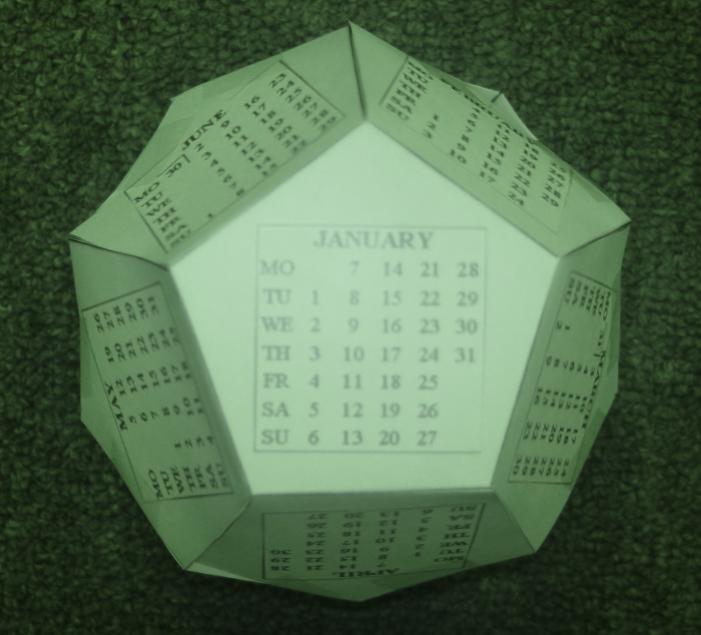
చిత్రము 6-3: ద్వాదశముఖి ఆకారములో 2008 క్యాలెండర్

ముగింపు

గొప్ప గణిత శాస్త్రజ్ఞుడు హెర్మన్ వేల్ (Herman Weyl) ఇలా అంటాడు – సామ్యరూపము లేక సౌష్ఠవమును మొట్ట మొదట చూస్తే సంబంధము లేనట్లు ఉండే ఎన్నో సిద్ధాంతాలకు, ఘటనలకు బాంధవ్యాన్ని తెచ్చి బెడుతుంది: భూ-అయస్కాంతశాస్త్రము, ఆడువారి మేలిముసుగులు, ధ్రువణ కాంతి, నైసర్గిక వరణము, వర్గ సిద్ధాంతము, తేనెతుట్టెలో ఈగల శ్రమవైఖరి, అంతరాళ నిర్మాణము, పూలనుంచే పాత్రల నమూనాలు, క్వాంటం భౌతిక శాస్త్రము, పేడపురుగులు, పూల రేకులు, ఎక్స్‌రే వ్యతికరణపు చిత్రాలు, సముద్రములోని అర్చినుల కణవిభజన, స్ఫటికములలోని అణువుల సమతా స్థితి, ఐరోపీయ ఆలయముల నిర్మాణము, హిమ స్ఫటికాలు, సంగీతము, సాపేక్షవాదము. అందుకే డార్సీ థాంప్సన్ ఇలా అంటాడు: దేవునికి జ్యామితి అంటే ఎంతో ప్రియము అనే నియమానికి మినహాయింపు లేదు!

సౌష్ఠవమును మనము చిత్రలేఖనము, శిల్పము, సాహిత్యము, సంగీతము ఇత్యాది లలితకళలలో చూస్తుంటాము. ఇది మనకు ఆనందాన్ని కలిగిస్తుంది, చైతన్యాన్ని కలిగిస్తుంది. కాని దీని మూలాధారము గణితశాస్త్రములోని సిద్ధాంతములు. ఈ సౌష్ఠవము లేని శాస్త్ర క్షేత్రమే లేదంటే అతిశయోక్తి కాదు. అందులోని కొన్ని సిద్ధాంతాలను ఈ ప్లేటో ఘనస్వరూపాల ద్వార మీకు పరిచయము చేసినాను. ఇది ఒక అనంతమైన గంభీరమైన మహాసాగరము. నేను మీకు చూపిందల్లా కొన్ని స్థిర చిత్రాలను మాత్రమే. ఇది మీ ఆసక్తి అనే దీపాన్ని వెలిగించి నూతన కాంతులను ప్రసరింప జేస్తుందని ఆశిస్తున్నా.

గ్రంథసూచి

1. ముగ్గులు – జెజ్జాల కృష్ణ మోహన రావు – కౌముది, జూన్ 2007
2. Order in space – A K Van der Vegt – 2001 – (Internet edition)
3. Platonic solids – Wikipedia
4. Platonic solids with animation
5. Synergetics – R Buckminster Fuller – Macmillan Publishing Company, New York, 1975
6. The new ambidextrous universe – Martin Gardner – W H Freeman Company, New York, 1990

ప్లేటో ఘనస్వరూపాలను శిల్పాలలో, భవనాలలో కూడ ఉపయోగించి ఉన్నారు. తోటలో (వింశతిముఖి), స్తంభాలపై (ఎడమవైపు వింశతిముఖి, కుడివైపు ద్వాదశముఖి), భవనములపై (అష్టముఖి), గ్రాహం బెల్ మ్యూసియంలో (చతుర్ముఖి), నీడగడియారపు నిర్మాణములో (sundial ద్వాదశముఖి), బాస్టన్ శిల్పములో (ద్వాదశముఖి) కొన్ని ప్లేటో ఘనస్వరూపాల చిత్రాలను చూడగలరు. మనుష్యులు ఉంటే జూదము కూడ ఉంటుంది, జూదము ఉంటే పాచికలు ఉంటాయి. సామాన్యముగా ఈ పాచికలు ఘన చతురస్రముయొక్క ఆరు ముఖాలుగా ఉంటాయి. అన్ని ప్లేటో ఘనస్వరూపాల ఆకారాలలో కూడ పాచికలు ఉన్నాయి!:
http://flickr.com/photo_zoom.gne?id=1739261130&size=lcc_license
http://flickr.com/photos/trappedinmatter/1390185956/
http://flickr.com/photos/black_wolf/1402955686/
http://flickr.com/photos/kikisdad/42960196/
http://flickr.com/photo_zoom.gne?id=1097634621&size=l
http://flickr.com/photo_zoom.gne?id=322885425&size=o
http://www.flickr.com/photo_zoom.gne?id=415339372&size=l