అవతారిక

ఆ మధ్య ఈమాట సంపాదకులు మాధవ్, “ఇన్నేళ్ళకి ఆండ్రూ వైల్స్ ఫెర్మా చివరి సిద్దాంతం సాధించి అందర్నీ ఒప్పించేరట. దాని మీద ఒక వ్యాసం రాయరాదూ?” అంటూ ఒక విద్యుల్లేఖ పంపేరు. “ఇటువంటి పనులు చేసే సామర్ధ్యం నాలో లేదు. నన్ను ఇబ్బంది పెట్టకండి,” అంటూ తిరుగు టపా పంపేను.

ఉత్తరం అంటే గీకి పారేసేను కాని, నిజంగా ప్రయత్నించి చూస్తే ఎలాగుంటుందో అన్న సందేహం నా మనస్సులో గొలకడం మొదలు పెట్టింది. ఈ సమస్యని కూలంకషంగా పరిశీలిస్తూ సైమన్ సింగ్ (Simon Singh) రాసిన ఫెర్మాస్ లాస్ట్ థియరమ్ అనే పుస్తకం కొని తెప్పించేను. ముందుకి, వెనక్కి నాలుగైదు సార్లు చదివేను. అర్థం కాని చోట్ల గూగుల్‌ని ఆశ్రయించేను. చదవగా, చదవగా ఒక విషయం అర్థం అయింది. ఇది నిజంగా అర్థం కావాలంటే గణితంలో ఒకటో, ఒకటిన్నరో పిహెచ్. డీ. పట్టాలు ఉండాలి. కొంచెం అర్థం అయితే చాలనుకునే వారికి అకుంఠితమైన పట్టుదల ఉండాలి. సైమన్ సింగ్ కూడ ఏదో బులబులాగ్గానే వివరించేడు; లోతుకి వెళ్ళలేదు. అలా సైమన్ సింగులా నేనూ బులబులాగ్గా చెప్పగలనా? ఆయన ఇంగ్లీషులో చెప్పేడు, నేను తెలుగులో చెప్పాలి. ఆయన 300 పేజీలలో చెప్పేడు. నేను ఏ 70 పేజీలలోనో చెప్పాలని కోరిక; అంత కంటె పొడుగుంటే తెలుగు పాఠకులు చదవరేమో అని ఒక బెంగ.

ఈ సమస్యని ఛేదించడానికి చేసిన ప్రయత్నాల చరిత్రలో స్థూలంగా రెండు దశలు ఉన్నట్లు అనిపించింది. మొదటి దశ గురించి మొదటి భాగంలో చెప్పేను; చెబుతున్న నాకు బాగానే అర్థం అయింది కనుక చదివే మీకూ అర్థం అయేటట్లు చెప్పడానికి ప్రయత్నించేను. రెండవ భాగంలో చెప్పిన రెండవ దశ లోని లోతైన విషయాలు నిజానికి నాకే పూర్తిగా అర్థం కాలేదు. సైమన్ సింగు కూడా తనకి అర్థం అయిందని దబాయించి చెప్పలేదు. అద్భుతమైన ప్రయత్నం మాత్రం చేసేడు. నేనూ అదే ధోరణిలో ప్రయత్నం చేసేను. సైమన్ సింగ్ ఇంగ్లీషులో సాధించిన దాంట్లో వందో వంతు నేను తెలుగులో సాధించగలిగితే నా ప్రయత్నం ఫలించినట్లే! ఇది సైమన్ సింగ్ రాసిన పుస్తకానికి అనువాదం కాదు. ఆయన సంతర్పణ కోసమని గుండిగలతో చేసి వడ్డించేడు. నేను పాళ్ళు తగ్గించి, మా వంటింట్లో కుంపటి సెగ మీద, నా పైత్యం అనే పోపు వేసి ప్రయత్నం చేస్తున్నాను.

చదువరులకి ఒక హెచ్చరిక! ఎంత కాదనుకున్నా గణిత సమీకరణాలు, గణిత భావాలూ వాడకుండా ఈ అంశం ప్రస్తావించడానికి వీలు పడదు. కనుక కొంత గణితం, కొంత గణిత పరిభాష తప్పనిసరి. కనీసం ఉన్నత పాఠశాలలో నేర్పే బీజగణితం పాటి గణితంతో పరిచయం లేకపోతే కొన్ని సందర్భాలలో నేను చెప్పేది అర్థం కాదు. అప్పుడు నిరుత్సాహ పడకుండా దున్నుకుంటూ పోతే మీ శ్రమ వృధా కాదని నా నమ్మకం.

వేమూరి వేంకటేశ్వరరావు.

మొదటి భాగం

xⁿ+yⁿ = zⁿ where n represents 3, 4, 5, …, has no solution.

“I have discovered a truly marvelous demonstration of this proposition which this margin is too narrow to contain.”

– Pierre de Fermat, 1601/1667 – 1665.

గణిత ప్రపంచంలో మూడు శతాబ్దాలకి పైబడి పరిష్కారం లేకుండా ఉండిపోయిన అతి జటిలమైన సమస్య ఏదయ్యా అంటే అది ఫెర్మా కదాచిత్తుగా ప్రవచించిన ఒక అభిప్రాయం. ఈ శిష్టుని అభిప్రాయం, ఫెర్మా చివరి సిద్ధాంతం (Fermat’s Last Theorem) అనే పేరుతో చలామణీ అవుతోంది. ఋజువు లేకుండా ఒక నిష్ణాతుడు వెలిబుచ్చిన అభిప్రాయం కనుక దీనిని నిజానికి ఫెర్మా శిష్టాభిప్రాయం (Fermat’s conjecture) అనాలి, అంటారు కూడానూ.

ఎవరీ ఫెర్మా? ఏమిటా శిష్టాభిప్రాయం? ఆ అభిప్రాయంలో ఉన్న జటిలత్వం ఏమిటి? ఈ సమస్య పరిష్కారం లేకుండా మూడు వందల ఏళ్ళు పైబడి ఎందుకు ఉండిపోయింది? చివరికి పరిష్కారం ఎలా దొరికింది?

మూడు వందల ఏళ్ళపాటు హిమవన్నగం అంత ఎత్తుకెదిగిన హేమాహేమీలు ప్రయత్నించినా పరిష్కారం లేకుండా ఉండిపోయిందంటే ఇది నిజంగా క్లిష్టమైన సమస్యే. ఇటీవల ఏండ్రూ వైల్స్ (Andrew Wiles) ఆవిష్కరించిన 130 పేజీల రుజువు గణితంలో ఏళ్ళ తరబడి కృషి చేసిన పండితులకే తేలికగా అర్థం కాదు. కాని ప్రయత్నిస్తే ఒక నఖ చిత్రంలా అయినా అర్థం అవుతుందేమో చూద్దాం.

1. పియేర్ డి ఫెర్మా (Pierre de Fermat)

పియేర్ డి ఫెర్మా (1601 – 1665)

పియేర్ డి ఫెర్మా (Pierre de Fermat) ఫ్రాన్స్ దేశపు బూమా్ డి లోమాన్య (Beaumont-de-Lomagne) ప్రాంతంలో పుట్టేడు; ఎప్పుడు పుట్టేడో ఇదమిత్థంగా తెలియదు (1601 లేదా 1607లో). ఒక అంచనా ప్రకారం, ఇతను ఇంకొక ఏడాదిలో పుడతాడనగా ఇంగ్లండులో ఈస్ట్ ఇండియా కంపెనీ స్థాపించడం, ఆ కంపెనీ ఇండియాతో వ్యాపారం చేసుకుందుకి అక్బర్ పాదుషా అనుమతి ఇవ్వడం జరిగింది. ఫెర్మా అయిదేళ్ళ పిల్లవాడప్పుడు అక్బర్ చక్రవర్తి మరణించేడు. అదీ ఈ కథనపు చారిత్రక నేపథ్యం.

పియేర్ తండ్రి డామినీక్ ఫెర్మా సామంతుడైన వ్యాపారస్తుడు కావడం వల్ల పియేర్‌కి మంచి పాఠశాలలో విద్యాభ్యాసం చేసే అవకాశం లభించింది. కాని విద్యార్థి దశలో ఫెర్మా ప్రతిభావంతుడైన గణిత శాస్త్ర వేత్తగా పరిణతి చెందుతాడనుకోడానికి దాఖలాలు కనిపించలేదు. ఇంట్లో పెద్దల ఒత్తిడి మీద న్యాయశాస్త్రం చదివి సర్కారీ నౌకరీలో చేరేడు. ప్రజలు దాఖలు చేసుకున్న అర్జీలని పరీక్షించి వాటిలో యోగ్యత కలవాటిని ఎంపిక చేసి ప్రభువుకి దఖలు పరచే ఉద్యోగం అది. ఫెర్మా ఆ ఉద్యోగాన్ని ఎంతో దక్షతతో, సమర్ధవంతంగా నిర్వర్తించేడు.

ఫెర్మా న్యాయ విచారణా వ్యవస్థలో తీర్పరిగా కూడ కొన్నాళ్ళు పని చేసేడు. ఈ విధి నిర్వహణలో ఒక మత పురోహితుడికి – తన విధ్యుక్త ధర్మాన్ని సరిగ్గా నిర్వర్తించలేదనే నేరంపై – సజీవ దహనశిక్ష (burning at the stake) విధించేడు కూడ.

ఈ రెండు ఉద్యోగాలు సుమారుగా భారత దేశం లోని మునసబు-మేజిస్ట్రేటు వంటివి. ఇలా సమాజపు నిచ్చెన మెట్లు ఒకటీ ఒకటీ ఎక్కుతూ చివరికి తన పేరులో డి (de) అనే పట్టపు పేరు తగిలించుకునే హక్కు కూడ సంపాదించుకున్నాడు. ఈ విజయాలన్నిటికి అతని చికీర్ష ఒక్కటే కారణం కాదు; దేశంలో ప్రజారోగ్య పరిస్థితులు కూడ కొంతవరకు దోహదం చేసేయి. ఆ రోజుల్లో ప్లేగు మహామారి యూరప్‌లో విస్తృతంగా వ్యాపించి ఎంతో మందిని పొట్టబెట్టుకుంది. ప్రభుత్వోద్యోగులు చనిపోయినప్పుడు ఆ ఖాళీలు భర్తీ చెయ్యాలి కదా. ప్లేగు వచ్చి కోలుకున్న కొద్ది వ్యక్తులలో ఒకడు కనుక ఫెర్మాకి ఖాళీ అవుతున్న ఆ పై ఉద్యోగాలలోకి జొరబడే అవకాశం వచ్చింది.

ఆనాటి ఫ్రాన్స్ లోని ఈతిబాధలలో పాడవుతూన్న ప్రజారోగ్య వాతావరణం ఒకటయితే అంతకంటె పాడుగా ఉన్న రాజకీయ వాతావరణం మరొకటి. ఫెర్మా ప్రాంతీయ శాసనసభకి నియామకం అయిన కొత్త రోజులలోనే కార్డినల్ రిషెలూ (Cardinal Richelieu) ఫ్రాన్స్‌కి ప్రధానమంత్రిగా నియామకం పొందేడు. కుట్రలు, కుతంత్రాలు, వెన్ను పోట్లు రివాజుగా జరిగే ఆ రోజులలో ఫెర్మా జీవితం అసిధారా వ్రతంలా ఉండేది. ‘నొప్పింపక, తానొవ్వక తప్పించుకు తిరుగువాడు ధన్యుడు సుమతీ’ అన్నట్టు ఆ నీతిని అక్షరాలా ఆచరించి, ఫెర్మా వృత్తిపరమైన తన పనులు తాను తల వంచుకుని చేసుకుంటూ, తీరిక సమయాలలో తన ప్రవృత్తి అయిన గణితంలో తారసపడే చిక్కు సమస్యలకి పరిష్కారాలు వెతికేవాడు. వృత్తి ప్రభుత్యోద్యోగం, వ్యావృత్తి గణితం. గణితాభిలాషి, గణితంలో ఔత్సాహికుడు అంటే ఇతనే అనే పేరు తెచ్చుకున్నాడు.

1.2 గణితంలో అభిలాష

పదిహేడవ శతాబ్దపు మొదటి రోజులలో గణిత శాస్త్రం ఇంకా చీకటి యుగంలోనే ఉందనవచ్చు. ఆ రోజులలో గణిత శాస్త్రజ్ఙులకి పెద్దగా పరపతి, పలుకుబడి ఉండేవి కాదు; ఏదో అంకెలతో గారడీలు చేసే వాళ్ళ కోవలో పరిగణించ బడేవారు. గలీలియో (Galileo Galilei) అంతటివాడికి పీసా విశ్వవిద్యాలయంలో గణితం చదవడానికి అవకాశం రాలేదు; బైట పాఠాలు చెప్పించుకుని నేర్చుకున్నాడు. అంతవరకు ఎందుకు? యూరప్ ఖండం అంతటికీ ఒక్క ఆక్సఫర్డ్ విశ్వవిద్యాలయం లోనే గణితానికి ఒక శాఖ, ఒక పీఠం, ఉండేవి.

ఫెర్మా నివసించిన ఊరు పేరిస్‌కి దూరం కావడంతో పేరిస్ నగరంలో ఉన్న కొద్దిపాటి గణిత వేత్తలు, ఉదా. పాస్కాల్ (Blaise Pascal), మెర్సెన్ (Marin Mersenne) కూడా నేరుగా అందుబాటులో ఉండేవారు కాదు.

ఫెర్మా ఉత్తర ప్రత్యుత్తరాలు జరిపిన వారిలో ఫాదర్ మెర్సెన్ ఒకరు. ఈయన కేథలిక్ చర్చిలో మతాధికారిగా ఉంటూనే ఆ కాలపు గలీలియో, రెనే డెకార్ట్ (Rene Descartes) వంటి పెద్దలతో ఉత్తరప్రత్యుత్తరాలు నడిపించేవారు. ఈయన ఫ్రాన్సులో తిరుగుతూ ఫెర్మాని తరచు కలుసునేవారు. ఫెర్మా స్నేహబృందంలో మెర్సెన్ ఒకరైతే, డయొఫాంటెస్ 3వ శతాబ్దంలో రాసిన అరిథ్మెటికా (Arithmetica) అనే పురాతన గ్రీకు గణిత గ్రంథం మరొకటని అభివర్ణించవచ్చు. మంచి పరిచయం ఉన్నప్పటికీ మెర్సెన్ వల్ల పూర్తిగా ప్రభావితుడు కాలేదు ఫెర్మా; తన ధోరణిలో తను సిద్ధాంతాలు – రుజువులు చూపించకుండా – కాగితాల మీద రాసి వదిలేసేవాడు. రుజువేది? అని అడిగితే, ‘నా బుర్రలో ఉంది’ అని సమాధానమిచ్చేవాడు. తను ఆవిష్కరించిన సిద్ధాంతాల వల్ల తనకి పేరు ప్రతిష్ఠలు రావాలని అతనికి ఉండేది కాదో లేక ఋజువులు అన్నీ వివరంగా రాసి చూపిస్తే తన రహస్యాలు బట్టబయలు అవుతాయన్న భయమో తెలియదు. దీనికి తోడు కొంత చిలిపితనం కూడ ఉండేదేమో అప్పుడప్పుడు తన అనుయాయులని అల్లరి పెట్టే ఉద్దేశంతో సిద్ధాంతం రాసి, రుజువు చూపించకుండా, ఇది అవునో కాదో చెప్పుకో చూద్దాం! అని సవాలు చేసి సమాధానం చెప్పేవాడు కాదు. రెనే డెకార్ట్ అంతటివాడు ఫెర్మాని గప్పాల గండడు అనేవాడు.

ఇలా సమస్యని ఇచ్చి పరిష్కారం ఇవ్వకుండా అందరిని ఆటపట్టించడంలా ఉన్నా ఈ వింత ప్రవర్తనలో కొన్ని లాభాలు కూడా ఉన్నాయనుకోవచ్చు. ఒకటి, ప్రతీ సమస్యకీ పరిష్కారం రాస్తూ కూర్చుంటే బోలెడు సమయం వెచ్చించవలసి ఉంటుంది. ఆ సమయంలో కొత్త సమస్యలు సృష్టించవచ్చు కదా! రెండు, సమస్యలకి పరిష్కారాలు రాసి ఇచ్చేస్తూ ఉంటే తెలిసీ తెలియని ప్రతి అనామకుడూ వచ్చి వాద ప్రతివాదాలలోకి దింపొచ్చు.

ఫెర్మా తనంత తానుగా చొరవతో ఉత్తరాల ద్వారా సంభాషణలు కొనసాగించినది ఇద్దరితో మాత్రమే: మెర్సెన్, పాస్కాల్. ఒక విధంగా, ఈ ఉత్తరాల ద్వారా ఫెర్మా, పాస్కాల్ సంభావ్యతా వాదం (Probability Theory) సౌథానికి పునాదులు వేసేరనవచ్చు. ఎక్కువమందికి తెలియని మరొక విషయం ఏమిటంటే ఫెర్మా కేల్‌క్యులస్‌కి వేసిన పునాదుల మీదే న్యూటన్ కేల్‌క్యులస్ మహా సౌధాన్ని నిర్మించేడు. ఈ విషయం న్యూటనే ఒప్పుకున్నాడన్న విషయం 1934 వరకు చాలమందికి తెలియనే లేదు; అందువల్ల ఫెర్మాకి దక్కవలసిన గుర్తింపు దక్కలేదు. కేల్‌క్యులస్‌కీ, సంభావ్య సిద్ధాంతానికీ ఫెర్మా వేసిన పునాదులు ఆయన పేరు చరిత్రలో చిరస్థాయిగా నిలచిపోడానికి సరిపోతాయి. ఈ రెండింటితోపాటు సంఖ్యా వాదానికి (Number Theory) కూడ ఫెర్మా మౌలికమైన పునాదులు వేసేడు.

ఫెర్మాకి గణితంలో గురువంటూ ఎవ్వరూ లేరు. అతని పరిశ్రమ అంతా అరిథ్మెటికా చదువుకుని స్వయంకృషితో చేసినదే. ఆ గ్రంథం వెయ్యేళ్ళ గణితసార సంగ్రహం. పైథాగరోస్, యూక్లిడ్ వంటి హేమాహేమీలు ఆవిష్కరించిన శాస్త్రం – ప్రత్యేకించి సంఖ్యా శాస్త్రం – అంతా ఆ గ్రంథంలో క్రోడీకరించబడి ఉంది. ఈ పుస్తకంలో ‘పులి-మేక-గడ్డిమేటు పడవలో నదిని దాటడం’ వంటి గణిత ప్రహేళికలు వందకి పైగా కనిపిస్తాయి. ప్రతీ ప్రహేళికనీ ఒక క్రమ పద్ధతిలో పరిష్కరించి చూపుతాడు డయొఫాంటెస్. కాని అదేమి (దుర్)అదృష్టమో కాని ఈ పుస్తకం చదివి గణితం నేర్చుకున్న ఫెర్మాకి ఈ పుస్తకం క్రమబద్ధం చేసిన మంచి అలవాటు అబ్బలేదు. ఏదైనా క్లిష్టమైన సమస్య ఎదురైనప్పుడు దానిని పరిష్కరించే పద్ధతిని ఒక చిన్న కాగితం మీద ముక్తసరిగా మూడు ముక్కలలో సూచించి, దానితో కొన్నాళ్ళు చెలగాటాలు ఆడి ఆ కాగితం ముక్కని చెత్త బుట్టలో పడేసేవాడు. అప్పుడప్పుడు, పక్కని కాగితం కనబడకపోతే, ఆ రాయదలుచుకున్నది ఆ పుస్తకం యొక్క ఉపాంతంలో (మార్జిన్) గొలికేవాడు. ఇలా ఉపాంతంలో రాసిన ఆణిముత్యాలు ఎన్నో తరవాత తరాలవారికి దొరికేయి; దొరికిన వాటన్నిటిని రుజువు చెయ్యడం సాధ్యపడింది కాని చివరికి ఒకటి రుజువు లేకుండా మిగిలిపోయింది. అందుకనే దానిని చివరి సిద్ధాంతం అంటారు.

1.3 ఫెర్మా చివరి సిద్ధాంతం

అరిథ్మెటికా యొక్క రెండవ సంపుటంలో ఫెర్మాకి పైథాగరోస్ సిద్ధాంతానికి సంబంధించిన ప్రహేళికలు ఎన్నో కనిపించేయి. పైథాగరోస్ సిద్ధాంతం తెలియనివాళ్ళు ఉండరంటే అది అతిశయోక్తి కాదు; చదవనేర్చిన ప్రతి వారికీ ఈ సిద్ధాంతంతో పరిచయం ఉంటుంది: ఒక లంబకోణ త్రిభుజంలో కర్ణం మీద నిర్మించిన చతురస్రపు వైశాల్యం మిగిలిన రెండు భుజాల మీద నిర్మించిన వైశాల్యాల మొత్తానికి సమానం. ఉదాహరణకి ఒక లంబకోణ త్రిభుజంలో మూడు భుజాల పొడుగులు 3, 4, 5 అయితే పైథాగరోస్ సిద్ధాంతం ప్రకారం:

3² + 4² = 5²

అవుతుంది. అందుకని ఈ {3,4,5} లని పైథాగొరోస్ త్రిపుటలు (Pythagoras triples) అంటారు. ఇటువంటి త్రిపుటలు ఇంకా ఉన్నాయా అన్న సందేహం రావడం సహజం. ఇటువంటి త్రిపుటలు ఇంకా చాలా ఉన్నాయి: {3,4,5}, {5, 12, 13}, {8, 15, 17}, వగైరాలు. నిజానికి ఇటువంటి త్రిపుటలు అనంతమైనన్ని ఉన్నాయని ఋజువు చెయ్యడం కష్టం కాదు. వీటిలో కొన్ని త్రిపుటలు ప్రత్యేక లక్షణాలని ప్రదర్శిస్తాయి. ఉదాహరణకి {20, 21, 29} అనే త్రయాన్ని కుంటి త్రిపుటలు అంటారు:

20² + 21² = 29²

వీటిని కుంటి అనడానికి కారణం ఈ త్రిభుజాన్ని బొమ్మలా గీసి, కర్ణం భూమి మీద పడేటట్లు అమర్చితే, 20, 21 పొడుగున్న (భుజాలు), ఎగుడు-దిగుడుగా, కుంటి భుజాల్లా కనిపిస్తాయి.

ఇలా పైథాగరోస్ త్రిపుటలతో చెలగాటాలు ఆడుతూన్న సమయంలో ఫెర్మాకి చిన్న సందేహం వచ్చింది. పైథాగరోస్ సిద్ధాంతాన్ని

x² + y² = z²

లా కాకుండా, కొద్దిగా మార్చి, ఈ దిగువ చూపిన విధంగా రాస్తే (అనగా 2 కి బదులు 3 వేసి రాస్తే)

x³ + y³ = z³

ఏమవుతుందీ అని. ఎంత ప్రయత్నించి చూసినా x, y, z స్థానాలలో ఏ పూర్ణ సంఖ్య వాడినా పై సమీకరణం చెల్లలేదు. అనగా ఘాతం స్థానంలో 2 ఉంటే అనంతమైనన్ని పరిష్కారాలు ఉన్నాయి కాని, ఆ ఘాతం స్థానంలో 3, 4, 5,… అలా మరే ఇతర పూర్ణాంకం వేసినా పై సమీకరణం చెల్లలేదు.

ఫెర్మా తల గోక్కున్నాడు. గోక్కుని, గోక్కుని, ఆ అరిథ్మెటికా పుస్తకం ఉపాంతంలో ‘ఈ సమస్యకి పరిష్కారం లేదని చెప్పడానికి అత్యద్భుతమైన రుజువు నా దగ్గర ఉంది కాని, రాసి చూపిద్దామంటే ఈ ఉపాంతంలో చోటు సరిపోదు,’ అని ముక్తసరిగా మూడు ముక్కలు రాసేసి, మనం అంతా ఆ నాలుగు ముక్కలూ చూసే వేళకి ఆయన అయిదు ప్రాణాలు వదిలేసి హరీమనిపోయేడు.

మనకి సమస్య మిగిలింది, రుజువు దొరకలేదు. ఉపాంతం కాసింత పెద్దదిగా ఉంటే ఆ రుజువేదో ఆయనే అక్కడ రాసి ఉండేవాడు కదా! కుర్రా పెద్దా ఆ సమస్యని సాధించడానికి నడుం కట్టుకుని రంగం లోకి దూకేరు. దూకి, మూడు వందల ఏళ్ళ పాటు నానా యాతనలూ పడ్డ తరువాత, చివరికి 23 జూన్ 1993న, ఏండ్రూ వైల్స్ (Andrew Wiles), రిచర్డ్ టేలర్ (Richard Taylor) సహాయంతో, 130 పేజీలు పొడుగున్న రుజువు రాసి మనని ఒక గట్టెక్కించి మన పరువూ మర్యాదా నిలబెట్టేరు. ‘ఫెర్మా ఉపాంతంలో రాసింది నిజమే సుమా!’ అంటూ అంతా ఆశ్చర్యపోయేరు. టనియామా (Yutaka Taniyama), షిమూరా (Goro Shimura) అనే ఇద్దరు జపనీయులు, ఇవరీస్ట్ గేల్వా (Evariste Galois) అనే ఫ్రాన్స్ దేశీయుడు చేసిన పనులు వెనకాతల దన్నుగా ఉండి ఉండకపోతే ఏండ్రూ వైల్స్ నిర్మించిన ఈ సౌధం సాధ్యపడేది కాదు.

‘రుజువు రాసి చూపిద్దామంటే ఈ ఉపాంతంలో చోటు సరిపోదు’ అన్న ఫెర్మా మాటలు ఓటి మాటలే అయినా, అవే ఆయనకి ఎక్కువ పేరు, ప్రఖ్యాతులు తెచ్చిపెట్టిన మాటలయేయి. విచిత్రం!

1.4 ఫెర్మా సిద్ధాంతపు ఉపయోగం

ఇంతమంది ఇన్నివందల ఏళ్ళు కష్టపడి పని చేసి ఋజువు సంపాదించేరంటే ఆ రుజువు వల్ల మానవ సమాజానికి ఏమిటి ఒరిగిందంటే నిజానికి ఏదీ లేదనే చెప్పాలి. గణితంలో కొన్ని కీలకమైన సిద్ధాంతాలు ఉన్నాయి. వాటిని రుజువు చెయ్యగలిగితే ఆ రుజువుల మీద ఆధారపడే ఇతర సమస్యలు ఎన్నో ఉంటాయి. కాని ఫెర్మా సిద్ధాంతం విషయంలో అటువంటి చిక్కులు ఏవీ లేవు. ఈ సిద్ధాంతం రుజువు కాకపోతే పుట్టి ములిగిపోదు, గణితం ప్రగతి పథంలో పరిగెట్టకుండా మరకట్టు వేసినట్లు ఆగిపోదు. కాని రుజువు లేకుండా సిద్ధాంతం ఉండిపోతే ఏమి మర్యాదగా ఉంటుంది? అందులోనూ సమస్య అందరికీ తేలికగా అర్థం అయే సమస్య. ఆ మాత్రం ఋజువు చెయ్యలేకపోతే నలుగురూ నవ్విపోరూ!

1.5 ఒక చారిత్రక సత్యం

ఒక లంబకోణ త్రిభుజంలో కర్ణం మీద నిర్మించిన చతురస్రపు వైశాల్యం మిగిలిన రెండు భుజాల మీద నిర్మించిన చతురస్రాల వైశాల్యాల మొత్తానికి సమానం అన్న దృగ్విషయం పైథాగొరోస్ పుట్టక పూర్వం నుండీ, ఒక సహస్రాబ్దం పాటు, అనేక దేశాలలో అనేక మందికి తెలుసు. భారతీయులకి తెలుసు, బాబిలోనియాలో తెలుసు, చైనాలో తెలుసు. కాని ఈ సూత్రం పైథాగొరోస్ పేరు మీదుగా నిలవడానికి ఒక ముఖ్య కారణం ఉంది. ఈ వెయ్యి సంవత్సరాల పాటూ పైన చెప్పిన సమాజాలలో వారికి వారి ఎదుటపడ్డ లంబకోణ త్రిభుజాల విషయంలో ఈ సూత్రం పని చేస్తుందని తెలుసు. కాని వారికి తారస పడని అనంతమైన లంబకోణ త్రిభుజాల విషయంలో కూడ ఈ సూత్రం పని చేస్తుందా అన్న ప్రశ్నని వారిలో ఎవ్వరూ వేసినట్లు లేదు. అంటే ఏమిటి? పైథాగొరోస్ అన్నది ఏమిటంటే,చదునుగా ఉన్న సమతలం మీద మనం గీయగలిగే ప్రతీ లంబకోణ త్రిభుజం – ఇవి అనంతమైనన్ని ఉన్నాయని మరచిపోకండి – విషయంలోనూ ఈ సూత్రం పని చేస్తుందని ఉద్ఘాటించేడు. ఆ త్రిభుజం మన ఎదురుగా ఉన్నా, లేకపోయినా, మనం దానిని చూసినా, చూడకపోయినా, ఈ లక్షణం ప్రదర్శించి తీరుతుందని ఆయన తార్కికంగా ఋజువు చేసేడు. అదీ కీలకం ఇక్కడ.

ఇదే విధంగా ఫెర్మా ఉపాంతంలో రాసిన శిష్టాభిప్రాయం x, y, zలు పూర్ణ సంఖ్యలై ఉండి, n అనేది 2 కంటె పెద్దదైన పూర్ణ సంఖ్య అయిన అన్ని సందర్భాలలోనూ చెల్లుతుందని రుజువు చెయ్యాలి. ఈ రుజువుని ఒక గట్టుకి చేర్చడానికి మూడు శతాబ్దాలకి పైగా వందల మంది గణితజ్ఞులు పాటు పడ్డారు. వారిలో కనీసం కొందరి కథైనా తెలుసుకోవాలి మనం.

2. లియొన్‌హార్డ్ ఆయిలర్ (Leonhard Euler)

లియొన్‌హార్డ్ ఆయిలర్ (1718-1781)

ఫెర్మా సిద్ధాంతం ఋజువు చెయ్యడానికి శ్రమించిన వారు చాల మంది ఉన్నారు కానీ ప్రగతి సాధించిన బహు కొద్దిమందిలో పదునెనిమిదవ శతాబ్దపు లియొన్‌హార్డ్ ఆయిలర్ (Leonhard Euler) ఆద్యుడు. ఆయిలర్ స్విట్జర్లండ్‌లో 1707లో పుట్టేడు. పుట్టుకతోటే గణితంలో పరిమళించడం మొదలు పెట్టినా ఇతని చేత ఎలాగైనా క్రైస్తవ మతధర్మశాస్త్రం చదివించాలని అతని తండ్రి పాల్ విశ్వ ప్రయత్నం చేసేడు. కాని గణితశాస్త్రపు అదృష్టం కొద్దీ అదే ఊళ్ళో ప్రతిష్ఠాత్మకమైన బర్నోలీ కుటుంబం ఉండడం జరిగింది. మూడు తరాల వ్యవధిలో ఈ బర్నోలీ వంశంలో ఎనిమిది దిగ్గజాలవంటి శాస్త్రవేత్తలు పుట్టుకొచ్చేరు. వీరిలో డేనియల్ బర్నోలీ, నికలస్ బర్నోలీ ఓయిలర్‌కి ఆప్తమిత్రులు కావడం మన అదృష్టం. ఒక ప్రతిభావంతుడైన గణితశాస్త్రవేత్త మత ధర్మశాస్త్రాలలోని డుకృంకరణాలని మననం చేస్తూ ఒక మూలని పడి ఉంటే అది మానవజాతికే తీరని నష్టం అని తండ్రి పాల్‌కి హితోపదేశం చేసి ఆయిలర్‌ని గణిత ప్రపంచానికి దక్కేలా చేసి పుణ్యం కట్టుకున్నారు, బర్నోలీ సోదరులు.

2.1 ఆయిలర్ వాడిన పధ్ధతి

ఎంత గడ్డు సమస్య ఎదురైనా ఆయిలర్ చిటికల మీద పరిష్కరించేవాడుట. కాగితం, కలం అవసరం లేకుండా లెక్క అంతా బుర్రలోనే చేసేసేవాడుట. ఆయిలర్‌కి ఫెర్మా సమస్య ఎదురైనప్పుడు ఆయన ఈ విధంగా ఆలోచించేడుట. ఫెర్మా ఏమన్నాడు?

‘చలరాసి n అనేది 2 కంటె పెద్దదయిన పూర్ణాంకం అయినప్పుడు, ఈ xⁿ + yⁿ = zⁿ సమీకరణం చెల్లదు,’ అన్నాడు.

నిజానికి పైన చూపిన ఒక్క సమీకరణం ఈ దిగువ చూపిన అనంతమైనన్ని సమీకరణాలతో సమానం:

x³ + y³ = z³ చెల్లదు (n = 3 అయినప్పుడు)

x⁴ + y⁴ = z⁴ చెల్లదు (n = 4 అయినప్పుడు)

x⁵ + y⁵ = z⁵ చెల్లదు (n = 5 అయినప్పుడు)
…
…
అలా, అలా అనంతం వరకు.

అనంతమైనన్ని సమీకరణాలని పరిశీలించడం ఎవ్వరి వల్ల అవుతుంది? వీటిలో ఏదో ఒకటి చెల్లదని రుజువు చేసి, అటుపైన అదే పద్ధతిలో మిగిలినవన్నీ చెల్లవని వాదిస్తే?

ఈ రకం ఆలోచన రావడానికి ఫెర్మాయే తన పుస్తకంలో, మరొక చోట, మరొక ఉపాంతంలో n = 4 అయిన సందర్భంలో పై సమీకరణం చెల్లదు అని రుజువు చెయ్యడం ఎలాగో దారి చూపించేడు. ఈ పద్ధతిని అనంతావతార పధ్ధతి (the method of infinite descent) అందాం. ఇదే దారి వెంబడి వెళుతూ n = 5, n = 6, … అని అన్ని సందర్భాలని పరిష్కరించుకుంటూ పోవచ్చు కదా అనుకున్నాడు ఆయిలర్. అనుకుని, ఈ పద్ధతి ఉపయోగించి ముందస్తుగా n = 3 సందర్భాన్ని పరిష్కరించి 1753లో తన ఫలితాన్ని ప్రకటించి ఫెర్మా సిద్ధాంతాన్ని నిరూపించే ప్రయత్నానికి పునాది రాయి వేసేడు. ఈ సందర్భంలో కాల్పనిక సంఖ్యలు, జంట సంఖ్యలు, లేదా యుగ్మ సంఖ్యలు (imaginary numbers) అనే భావం ఉపయోగించకుండా రుజువుని బందోబస్తుగా ముందుకి కదపడం సాధ్యపడలేదు. కాని ఇదే పధ్ధతి ఉపయోగించినప్పుడు n = 5, n = 6, … సందర్భాలు లొంగలేదు. అంటే ఫెర్మా n = 4 సందర్భాన్ని, ఆయిలర్ n = 3 సందర్భాన్ని లొంగదీసుకున్నారు కాని మిగిలిన (అనంతమైన) సందర్భాలు (n = 5, n = 6, …) లొంగలేదు; పరిష్కారం లేకుండా ఉండిపోయాయి.

అలాగని పరిస్థితి స్తంభించిపోయి ఆగిపోనూ లేదు. ఉడతాభక్తిగా పునాదులలో తలొకరు తలొక రాయి వెయ్యడం మొదలు పెట్టేరు. ఉదాహరణకి n = 4 సందర్భంలో సమస్య లొంగింది కనుక n = 8, n = 12, n = 16, n = 20, …, వగైరా సందర్భాలన్ని కూడ లొంగినట్లే అని రుజువు చెయ్యడం కష్టం కాదు. అదే విధంగా n = 3 సందర్భంలో సమస్య లొంగింది కనుక n = 6, n = 9, n = 12, n = 15, …, వగైరా సందర్భాలన్ని కూడ లొంగినట్లే అని రుజువు చెయ్యడం కష్టం కాదు. అంటే ఏమిటన్నమాట? ఫెర్మా, ఆయిలర్లు వేసిన పునాదుల మీద n = 3, 4, 6, 8, 9, … వగైరాలు ఉన్న సందర్భాలలో రుజువు దొరికినట్లే భావించవచ్చు.

ఇప్పుడు మనం గమనించవలసినది 3 యొక్క ప్రత్యేకత; 3 ఒక ప్రధాన సంఖ్య. ఏ సంఖ్య అయినా 1 చేత, తన చేత తప్ప మరే ఇతర సంఖ్య చేత నిశ్శేషంగా భాగహారానికి లొంగక పోతే ఆ సంఖ్యని ప్రధాన సంఖ్య అంటారు (1 ని మినహాయించి). కనుక 2, 3, 5, 7, 11, 13, …, అనుకుంటూ నిర్విరామంగా, అనంతవాహినిలా వచ్చే సంఖ్యలు అన్నీ ప్రధాన సంఖ్యలే. రసాయన శాస్త్రంలో అణువులు ఎలాంటివో గణితంలో ప్రధాన సంఖ్యలు అలాంటివి. ఉదాహరణకి, ప్రధాన సంఖ్యలు కానివి అయిన మరే ఇతర సంఖ్యని అయినా సరే కొన్ని ప్రధాన సంఖ్యల లబ్దంగా, ఒక ఏకైక (unique) పద్ధతిలో, రాయవచ్చు. మచ్చుకి:

8 = 2 x 2 x 2
18 = 2 x 3 x 3
21 = 3 x 7
35 = 5 x 7 వగైరా.

దీనినే అంకగణితపు ప్రాథమిక సిద్ధాంతం (The Fundamental Theorem of Arithmetic) అంటారు. ఈ సిద్ధాంతం మనకి యూక్లిడ్ రోజుల నుండీ తెలుసు. కనుక ఫెర్మా సిద్ధాంతం n ప్రధాన సంఖ్య అయిన సందర్భాలలో చెల్లుతుంది అని రుజువు చేస్తే మిగిలిన సందర్భాలలో కూడ రుజువు అయినట్లే కదా!

అంటే ఏమిటన్నమాట? ఫెర్మా సిద్ధాంతాన్ని అనంతవాహినిలా వచ్చే n = 1, 2, 3, 4, 5, 6, … ప్రతి ఒక్క సందర్భంలోనూ పరీక్షించి చూడక్కర లేదు; ఈ శ్రేణిలో వచ్చే ప్రధాన సంఖ్యలని మాత్రం పరీక్షించి చూస్తే చాలు. ఈ శ్రేణిలో వచ్చే ప్రధాన సంఖ్యలు 2, 3, 5, 7, 11, 13, … వగైరాలు ఎన్ని ఉన్నాయి? అవీ అనంతంగానే ఉన్నాయి! కనుక మనం పడవలసిన కష్టం ఏమీ తగ్గినట్లు లేదు కానీ ప్రతీ అల్లాటప్పా సంఖ్యనీ పరీక్షించి చూడక్కర లేదు – ఏదో గుడ్డిలో మెల్ల!

2.2 రామానుజన్ సంఖ్య 1729

ఎస్. రామానుజన్ (1887 – 1920)

ఈ సందర్భంలో శ్రీనివాస రామానుజన్ టేక్సీ సంఖ్య 1729ని ఒకసారి సందర్శించడం అప్రస్తుతం కాదు. మనందరికీ తెలుసున్న కథే కాని చిన్న మెలికతో చెబుతాను. రామానుజన్ సుస్తీగా ఉంటే హార్డీ పలకరించడానికి టేక్సీలో వెళ్ళేరు. వెళ్ళి, రామానుజన్‌తో, ‘నేను వచ్చిన టేక్సీ సంఖ్య 1729 – చాల చప్పగా ఉంది,’ అన్నారు. ‘ఛ! ఛ! అది చప్పదంటారేమిటి? అది చాల ఆసక్తికరమైన సంఖ్య. రెండు పూర్ణ సంఖ్యల ఘనాల మొత్తంగా, రెండు విధాలుగా, రాయగలిగే సంఖ్యలలో ఇది అతి చిన్న సంఖ్య,’ అన్నాడుట రామానుజన్! అనగా:

9³ + 10³ = 12³ + 1³ = 1729

ఈ సమీకరణాన్ని ఈ దిగువ విధంగా కూడ రాయవచ్చు.

9³ + 10³ = 12³ + 1

కదా? తత్ఫలితంగా వచ్చిన పై సమీకరణంలో చివర ఉన్న 1ని మినహాయిస్తే, మిగిలినది ఫెర్మా ఇచ్చిన సమీకరణంతో (n = 3 అయిన సందర్భంలో) సరిపోయింది కదా! అనగా, ఈ ఒక్క సందర్భంలోనూ ఫెర్మా సిద్ధాంతం వీగి పోకుండా దరిదాపు నిలబడినట్లే కదా! మరొక ఉదాహరణగా:

65601³ + 67402³ = 83802³ +/- 1

ఈ ఉదాహరణలో +/- అంటే, సమీకరణం నిక్కచ్చిగా చెల్లడానికి 1 కలపడమో, 1 తీసివెయ్యడమో చెయ్యాలి – అని అర్థం. ఇలా దరిదాపుగా చెల్లే ఉదాహరణలు (1 ఇటూ అటుగా సరిపోయేవి) రామానుజన్ పోయిన నోటు పుస్తకంలో (Ramanujan’s Lost Notebook) చాల ఉన్నాయిట. దీనిని బట్టి ఈ సమస్య పరిష్కారానికి రామానుజన్ కూడ వేలు పెట్టేడు అని మనం అనుకోవచ్చా? ఈ విషయం మరొక సందర్భంలో మళ్ళా ప్రస్తావిస్తాను.

3. సోఫీ జెర్మైన్ (Marie-Sophie Germain)

పందొమ్మిదవ శతాబ్దం ఆరంభమయే సమయానికి గణిత ప్రపంచంలో ఫెర్మా ప్రవచించిన చివరి సిద్ధాంతం ఒక కొరకరాని కొయ్య అనే పేరుని సంతరించుకుంది. లొంగకుండా అల్లరి పెడుతూన్న ఈ సిద్ధాంతాన్ని సాధించే నిర్మాణక్రమానికి ఆయిలర్ శంకుస్థాపన చేసి, ఒక పునాది వేసి, అప్పటికే చాల సంవత్సరాలు గడచిపోయింది.

3.1 వివక్ష వాతావరణంలో అబల చేసిన సాహసం

స్త్రీల పట్ల వివక్ష చూపుతూ, స్త్రీల జీవితం పిల్లలని కనడానికి, వంట ఇంటికి పరిమితం అనే పురుషాధిక్య, సంకుచిత భావాలతో విర్రవీగే ఫ్రెంచి సమాజంలో మరీ-సోఫీ జెర్మైన్ (Marie-Sophie Germain) పుట్టింది. గణితం వంటి శాస్త్రాలు అధ్యయనం చెయ్యగలిగే మేథోసంపత్తి స్త్రీలకి లేదని ఆ రోజుల్లో యూరప్ లోనూ, ప్రత్యేకించి ఫ్రాన్స్ లోనూ ఒక గాఢ విశ్వాసం ఉండేది. ఇటువంటి వాతావరణంలో సోఫీ జెర్మైన్ ఆకాశంలో అకస్మాత్తుగా వెలిగిన నవ్యతారలా ప్రకాశిస్తూ ఫెర్మా చివరి సిద్దాంతాన్ని పరిష్కరించడానికి ఒక విప్లవాత్మకమైన దిశానిర్దేశం చేసింది. గణితంలో ఆమె సాధించిన ఫలితాలని ప్రచురించడానికి మగ పేరు పెట్టుకుని దొంగచాటుగా బతకవలసి వచ్చిన ఆ రోజులలో కాకతాళీయంగా ఒక అనూహ్యమైన సంఘటన జరిగి ఉండకపోతే ఈమె అసలు పేరు మనకి తెలిసి ఉండేది కాదేమో!

సోఫీ జెర్మైన్ (1776 – 1831)

సోఫీ జెర్మైన్ ఆంబ్రోస్-ఫ్రాంఁస్వా జెర్మైన్ అనే వ్యాపారస్తుని కూతురు. ఆమెకి 13 సంవత్సరాల వయస్సప్పుడు ఫ్రెంచి విప్లవం పరాకాష్ఠ చేరింది. బేస్టీల్ (Bastille) దుర్గం పతనం అయిపోయి, దేశం అంతా విప్లవ వాతావరణంతో అల్లకల్లోలంగా ఉండడంతో ఈమె ఇల్లు వదలి బయటకి వెళ్ళే అవకాశమే ఉండేది కాదు. ఇంట్లో కాలక్షేపానికి లెక్కల పుస్తకాలు చదువుతూ కూర్చునేది. ఆ రోజులలో ఫ్రాన్స్‌లో రెండు రకాల లెక్కల పుస్తకాలు ఉండేవి: ఒకటి మగధీరులకి, రెండు అబలలకి. మగవారి కోసం రాసిన పుస్తకాలలో నిర్వచనాలు, సిద్ధాంతాలు, ఋజువులు, తర్కం, వగైరా లోతైన భావ పరంపరతో ఉంటే ఆడవారి కోసం రాసే పుస్తకాలు ప్రశ్నోత్తరాల రూపంలో, కొంచెం నాటకీయంగా, ఉండేవి. ఉదాహరణకి న్యూటన్ గురుత్వాకర్షణ సిద్ధాంతం లోని విలోమవర్గ సూత్రం (inverse square law) వివరించడానికి ‘ప్రియుడు ప్రియురాలిని విడచి 8 రోజులు ఉన్నాడంటే వారి మధ్య విరహవేదన 8×8 = 64 రెట్లు పెరిగినట్లన్న మాట,’ వంటి ఉపమానాలు వాడేవారు – ఆడవారికి ఆ భాష తప్ప మరొక విధంగా చెబితే అర్థం కాదన్న భావనతో. కాని సోఫీని ఆకట్టుకున్నది మరొక రకం పుస్తకం; జాఁ మాంటుక్లా (Jean Montucla) రాసిన గణితశాస్త్రపు చరిత్ర. అందులో ఆర్కిమిడీస్ కథ చదివి ఆమె నిర్విణ్ణురాలయింది. ఆర్కిమిడీస్ ఆవిష్కరించిన అనేక కొత్త విషయాలు ఆమెలో కుతూహలాన్ని రేకెత్తించిన విషయం నిజమే కాని, ఆర్కిమిడీస్ మరణించిన తీరు చదివి ఆమె చకితురాలయింది. ఆర్కిమిడీస్ జీవితకాలం అంతా ప్రశాంతంగా సిరక్యూస్ నగరంలో తన పరిశోధనలలో ములిగి తేలుతూ గడిపేడు. ఆయన డెబ్బయ్యో పడిలో పడ్డ తరువాత ఇసకలో, పుల్లతో ఏదో రేఖా చిత్రం గీసి, దానిని తదేక దీక్షతో చూస్తూ, ఆలోచనలో పడి బయటి ప్రపంచాన్నే మరచిపోయేడు. ఆ సమయంలో సిరక్యూస్ మీద దండయాత్ర చేస్తూ అక్కడకి వచ్చిన ఒక రోమన్ సైనికుడు, నువ్వు ఎవ్వరివి? నీ సమాచారం ఏమిటి? అంటూ ఏవో ప్రశ్నలు వేసేడుట. ఆలోచనలో ముణిగిపోయిన ఆర్కిమిడీస్ ఈ సైనికుడి రాకనే గమనించలేదుట. ఏకాగ్రతలో ఉన్న ఆర్కిమిడీస్‌కు సైనికుని ప్రశ్నలే వినిపించి ఉండవు. పదే పదే అడిగినా తన ప్రశ్నకి సమాధానం రాకపోయేసరికి ఆ సైనికుడు ఆగ్రహావేశంతో ఆర్కిమిడీస్‌ని బల్లెంతో పొడిచి చంపేసేడుట!

చేస్తూన్న లెక్క గురించి ఆలోచిస్తూ – తన ప్రాణానికే ముప్పు రాబోతూందనే విషయాన్ని కూడ గమనించకుండా – ఒక వ్యక్తీ ప్రపంచాన్నే మరిచిపోయేడంటే గణితంలో ఏదో ఆకర్షణ ఉండి ఉండాలి అని తర్కించుకుని గణితశాస్త్రాన్ని లోతుగా తరచి చూడాలని నిశ్చయించుకుంది సోఫీ. ముందు సంఖ్యా శాస్త్రం మీద మోజు చూపింది. క్రమేణా కేల్‌క్యులస్ కూడ స్వయంకృషితో నేర్చుకుంది. నడిరాత్రి వరకు దీపం దగ్గర కూర్చుని ఆయిలర్, న్యూటన్ ప్రభృతులు రాసిన పుస్తకాలు ఆపోశన పట్టేసింది. ఇంటి దగ్గర ఇంటి పనులు చేసుకుంటూ ఉండవలసిన పిల్ల రాత్రి, పగలు ఇలా గణితం అధ్యయనం చెయ్యడం ఆమె తండ్రికి నచ్చలేదు. రాత్రి పూట చదవడానికి వీలు లేకుండా ఇంట్లో కొవ్వొత్తులు సోఫీ కంట పడకుండా దాచేసేవాడు. గదిలో వేడి లేకుండా చేసేసేవాడు. తండ్రి చేస్తూన్న కుట్రని పసికట్టి తండ్రికి తెలియకుండా కొవ్వొత్తులు గదిలో దాచుకుని, తలుపు మూసుకుని, ఆ చలిలోనే, చదువుకునేది. హిరణ్యకశిపుడు ప్రహ్లాదుడిని బాధలు పెట్టినట్లు తండ్రి ఎంతలా నిరుత్సాహ పరచినా వాటన్నిటికి తట్టుకుని ఒళ్ళు మరచి గణితం అధ్యయనం చేసేది. చివరికి తల్లిదండ్రులు ఓటమిని ఒప్పుకుని సోఫీ గణితం చదువుతూ ఉంటే అభ్యంతరం పెట్టడం మానేసేరు. సోఫీ వివాహం చేసుకోకుండా జీవితాన్ని గణితానికే అంకితం చేసింది. ఒకప్పుడు అభ్యంతరం పెట్టిన తండ్రే ఇప్పుడు ఆమె ఉదర పోషణకి, పరిశోధనా పోషణకి బాధ్యత తీసుకున్నాడు. సోఫీ గణితంతో ఒంటరి పోరాటం కొనసాగించింది.

ఈ లోగా 1794లో పేరిస్‌లో ఇకోల్ పోలీటెక్నిక్ (Ecole Polytechnique) అనే ప్రతిష్ఠాత్మకమైన విశ్వవిద్యాలయం స్థాపించడం జరిగింది. ఇక్కడ గణితం, భౌతిక, రసాయన శాస్త్రాలు, సాంకేతిక విద్యలు మొదలైన అంశాలని పరిశోధించి, బోధించాలని, అడిగిన వారందరికీ పాఠ్యాంశాలు సరఫరా చెయ్యాలని వ్యవస్థాపకుల ఆశయం. కాని ఇక్కడ స్త్రీలకి ప్రవేశార్హత లేదన్నారు. సహజంగా బిడియస్తురాలైన సోఫీకి అధికారులని ఎదుర్కొని ప్రశ్నించే సాహసం లేదు. కాని అక్కడకి వెళ్ళి చదువుకోవాలనే తపన తగ్గలేదు. అందుకని అంట్వాన్ అగస్ట్ లి బ్లాంక్ అనే మాజీ విద్యార్థి పేరుని, అభిజ్ఞానాన్ని తస్కరించి అతని పేరు మీద దరఖాస్తు పడేసింది. ప్రవేశం లభించింది. పాఠాలు, పాఠ్య పుస్తకాలు, ఇంటి దగ్గర పని చేసి పరిష్కరించవలసిన సమస్యలు, వగైరాలు అన్నీ లి బ్లాంక్‌కి సరఫరా చేస్తున్నారు అధికారులు. ఇంటి పని, పరీక్షలు, అన్నీ లి బ్లాంక్ పేరు మీదుగా జరుగుతున్నాయి. ప్రతి వారం సోఫీ దాఖలు పరుస్తూన్న జవాబులు గణిత శాస్త్రపు ఆచార్యుడు, ఆ రోజుల్లో గణిత శిరోమణి అనదగ్గ జోసెఫ్-లూయీ లగ్రాంజ్ (Joseph-Louis Lagrange) దృష్టిలోకి వచ్చేయి. ఆశ్చర్యం! గత సంవత్సరం బొటాబొటీగా, అత్తెసరు మార్కులతో, నెట్టుకొచ్చిన లి బ్లాంక్ ఈ ఏడు వికసించి పరిమళిస్తున్నాడు! ఒక సారి వచ్చి తనతో ముఖాముఖీ మాట్లాడమని లి బ్లాంక్‌కి వర్తమానం పంపేరు. ఇక గత్యంతరం లేక సోఫీ ముసుగు తీసి బయట పడక తప్పలేదు. లగ్రాంజ్ అపరిమితానందంతో సోఫీని ఆహ్వానించి అక్కున చేర్చుకున్నాడు. ఇన్నాళ్ళకి తన ప్రతిభని గుర్తించగలిగే గురువు దొరికినందుకు, అతను ఆమెని ఆదరించి ఆశీర్వదించినందుకు సోఫీ ఆనందానికి హద్దు లేదు. అప్పటికి సోఫీ వయస్సు 20 సంవత్సరాల లోపే!

ఫ్రీడ్రిక్ గౌస్ (1777 – 1855)

ఇలా అనుకోకుండా ఎదురైన సంఘటనతో సోఫీ ఆత్మవిశ్వాసం పెరిగింది. పాఠ్యాంశాల పరిధుల్ని దాటి సాహసోపేతంగా గణితంలో కొత్త పుంతలు తొక్కడం మొదలు పెట్టింది. ప్రత్యేకించి సంఖ్యాశాస్త్రం లోతులు తరచి చూస్తూ ఉంటే ఫెర్మా చివరి సమస్య ఎదురయింది. కొన్ని ఏళ్ళు శ్రమించిన తరువాత ఆమె కంటికి ఆశాజనకంగా ఉన్న సరికొత్త మార్గం పొడచూపింది. ఉబికి వస్తున్న ఈ ఊహాస్రవంతిని ఎవ్వరితో పంచుకోవాలి? ఇంకెవ్వరు? గణిత పర్వత పంక్తులలో ఉత్తుంగ శిఖరాగ్రం వంటి జెర్మనీ దేశపు కార్ల్ ఫ్రీడ్రీక్ గౌస్(Carl Friedrich Gauss). గణిత సామ్రాజ్యానికి చక్రవర్తి ఆయన. యూక్లిడ్ ఎలిమెంట్స్ తరువాత అంత ప్రతిష్ఠాత్మకమైన పుస్తకం రాసేడు గౌస్. వ్యాసోచ్ఛిష్టం జగత్ సర్వం అని మనం అనుకున్నట్లే గణిత ప్రపంచంలో గౌస్ స్పృశించని శాఖ లేదు. కాని ఫెర్మా ఆఖరి సిద్ధాంతం గురించి ఆయన అస్సలు పట్టించుకోనే లేదు. ‘నీ అంతటి వాడు ఈ సమస్యని ఛేదించాలి’ అంటూ హైన్రిక్ ఓల్బెర్స్ (Heinrich Olbers) అభ్యర్ధిస్తే, ‘ఈ రకం పనికిమాలిన సమస్యలు నా కుతూహలాన్ని రేకెత్తించవు. కావలిస్తే ఇటువంటి సమస్యలని పుంఖానుపుంఖంగా ప్రతిపాదించగలను,’ అంటూ తిప్పికొట్టేడాయన. మూడొంతులు గౌస్ కూడ ఈ దిశలో ప్రయాణించి, ఫలితం కనిపించక, నిరాశతో అందని ద్రాక్ష పుల్లన అన్న మనస్తత్త్వం ప్రదర్శించేడేమో! మనకి తెలియదు. ఇటువంటి నేపథ్యంలో సోఫీ రాసిన జాబుని గౌస్ అందుకున్నాడు. చదివేడు. అందులో కనిపించిన కొత్తదనానికి ఆశ్చర్యపడి అంతవరకు ఈ సమస్యపై తాను ఏర్పరచుకున్న తూష్ణీభావాన్ని కాసింత సడలించి ఈ ప్రశ్నని మరొకసారి పరిశీలించడానికి మొగ్గు చూపేడు.

డెబ్భయి అయిదు సంవత్సరాల క్రితం ఆయిలర్ ఈ సమస్యని పరిష్కరించే ప్రయత్నంలో మొట్టమొదటి తప్పటడుగు వేసేడు: n = 3 అయిన ఒక్క సందర్భంలో ఈ సమస్యకి పరిష్కారం లేదు అని ఆయన ఋజువు చేసేరు. అటు తరువాత ఇతరులు ఇతర ప్రత్యేక సందర్భాలని, ఒకటీ ఒకటీ చొప్పున పరిశీలించి నేతి, నేతి (ఇది కాదు, ఇది కాదు) అనుకుంటూ తప్పటడుగులు వేసేరు. సోఫీ రంగంలోకి ప్రవేశించి, ఇలా ఒకటీ ఒకటీ సందర్భాల్ని సందర్శిస్తూ పోతే అనంత వాహినిలా ఉన్న సందర్భాలన్నిటిని సందర్శించి పరిష్కరించడం తెమిలే పని కాదు. ఒక్కుమ్మడిగా అనేక సందర్భాలని ఒకేసారి తీసుకుని అవన్నీ పరిష్కరించలేమని ఒక్క దెబ్బతో రుజువు చేస్తే పోలా? అనుకుని ఒక కొత్త పుంత తొక్కింది.

సోఫీ తొక్కిన మార్గాన్ని టూకీగా చెప్పడానికి ప్రయత్నం చేస్తాను. ఒక ప్రత్యేక లక్షణం ఉన్న p అనే ప్రధాన సంఖ్యని తీసుకుందాం. ఏమా ప్రత్యేక లక్షణం? p ప్రధాన సంఖ్య అయినప్పుడు (2p +1) కూడ ప్రధాన సంఖ్య అవాలి. ఉదాహరణకి p = 5 అయినప్పుడు 2p + 1 = 11 అయింది కదా. ఇక్కడ 5, 11 ప్రధాన సంఖ్యలే. ఈ లక్షణం ఉన్న జంటలని సోఫి జెర్మైన్ గౌరవార్థం జెర్మైన్ ప్రధాన సంఖ్యలు (Germaine primes) అంటారు.

ఇప్పుడు ఫెర్మా చివరి సిద్ధాంతంలో n = p అయిన ప్రత్యేక సందర్భాలన్నిటిలో (అనగా n జెర్మైన్ ప్రధాన సంఖ్య అయిన సందర్భాలలో, ఇవి అనంతం అయినన్ని ఉన్నాయి) ఫెర్మా సిద్ధాంతం చెల్లుతుంది అని రుజువు చేసింది. ఈ రుజువు ఎలా సాగుతుందో ఇప్పుడు చెప్పి సాధించేది లేదు కాని, గమనించవలసిన విషయాలు రెండు ఉన్నాయి. మొదటిది, ఫెర్మా చివరి సిద్ధాంతంలో n = 3, 4, 5, 6, 7, … అనుకుంటూ అనంతమైనన్ని సందర్భాలని మనం తనిఖీ చేసి రుజువు చేసుకుంటూ వెళ్ళాలి. ఈ వరుస క్రమంలో 3, 5, 7, 11, 13, 17, … వగైరాలు ప్రధాన సంఖ్యలు. ఈ ప్రధాన సంఖ్యలు అనంతమైనన్ని ఉన్నాయి. ఈ అనంత శ్రేణిలో సోఫి జెర్మైన్ పేరు మీదుగా చలామణీ అవుతూన్న జంటలు ఒక భాగమే. సోఫీ చూపిన రుజువు ఈ భాగానికే పరిమితం. మిగిలిన సందర్భాల సంగతి ఇక్కడ ప్రస్తావించడం లేదు. రెండవది, జెర్మైన్ జంటలు అనంతమైనన్ని ఉన్నాయి. కనుక సోఫీ ఒక్క వేటున అనంతమైనన్ని సందర్భాలని రుజువు చేసేరన్న విషయం విస్మరించకూడదు. అంటే ఏమిటన్నమాట? సోఫీ అనంతమైనన్ని సందర్భాల్ని ఒక్క వేటున పరిష్కరించినా, ఇంకా అనంతమైనన్ని సందర్భాలు పరిష్కారం లేకుండా మిగిలిపోయాయి. పూర్ణమదః పూర్ణమిదం … శ్లోకం ఒక సారి గుర్తుకి తెచ్చుకొండి.

తరువాత డిరిక్లే (Peter Dirichlet), లెజాండర్ (Adrien-Marie Legendre), ఎవరికీ వారుగా n = 5 సందర్భాన్ని రుజువు చేసేరు. తరువాత గేబ్రియల్ లమే (Gabriel Lamé) n = 7 సందర్భాన్ని ఋజువు చేసేరు. n=7 జెర్మైన్ సంఖ్య కాదు కనుక ప్రత్యేకంగా ఋజువు కావలసి వచ్చింది. ఈ రెండు సందర్భాలని కొంచెం లోతుగా తరచి చూసే ముందు, చిన్న పిట్టకథ.

3.2 గౌస్‌తో పరిచయం

సోఫీ గౌస్‌కి ఉత్తరం రాసే వేళకి ఆమె వయస్సు 20 సంవత్సరాలు. ఆడ పేరుతో జాబు రాస్తే గౌస్ చదవడేమోననే భయంతో ఆమె లి బ్లాంక్ అనే సంతకం పెట్టింది. గౌస్ సమాధానం రాసినప్పుడు మిస్టర్ లి బ్లాంక్ అని సంబోధిస్తూనే రాసేడు.

విధి పోకడ వెయ్యి విధాలు అంటారు. నెపోలియన్ ప్రష్యా మీదకి దండెత్తి ఉండకపోతే మనకి ఈ రోజున సోఫి జెర్మైన్ పేరు ఈ సందర్భంలో తలుచునే అవకాశమే వచ్చి ఉండేది కాదేమో! సా. శ. 1806లో నెపోలియన్ ప్రష్యా మీద దండెత్తినప్పుడు అతని సేనావాహినుల పాదాల కింద జెర్మనీ లోని పట్టణాలు ఒకటొకటీ పేక మేడలలా కూలిపోతున్నాయి. రోమన్ సైనికుల చేతులలో ఆర్కిమిడీస్‌కి పట్టిన గతే ఫ్రెంచి సైనికుల చేతులలో గౌస్‌కి పడుతుందేమోనని సోఫీ ఆరాట పడింది. అలాంటి దిగ్గజం ఒక సాధారణ సైనికుడి చేతులలో కూలిపోతే ఎవరికి నష్టం? అందుకని నెపోలియన్ సైన్యంలో పెద్ద హోదాలో ఉన్న తన స్నేహితుడు అయిన జనరల్ జోసెఫ్-మరీ పెర్నెటీకి స్వహస్తంతో ఉత్తరం రాసి పంపింది – గౌస్ ప్రాణానికి హాని కలగకుండా హామీ ఇమ్మని. ముందుకి కదులుతున్న సైన్యానికి గౌస్ ఎదురు పడ్డప్పుడు ఆయనకి ఎటువంటి హాని కలగకుండా చూసి, ‘అయ్యా! మీ ప్రాణం కాపాడింది మేము కాదు – మేడమ్ సోఫి జెర్మైన్ కోరిక’ అని చెప్పగానే గౌస్ ఈ సోఫి జెర్మైన్ ఎవ్వరో తెలియక చకితుడయ్యాడు.

గౌస్ ప్రాణంతో బయట పడ్డందుకు ఆయనని అభినందిస్తూ సోఫి జెర్మైన్ తన సొంత పేరుతో సంతకం పెట్టిన లేఖ చూసుకుని ఆయన ఎంతగానో సంతోషించి ఆమెకి ధన్యవాదాలు చెబుతూ లేఖ రాసేడు.

3.3 సువర్ణ పతకానికి పోటీ

సోఫీ చూపిన దారి వెంట వెళితే విజయం తథ్యం అనే నమ్మకంతో ఫ్రాన్స్‌లో అకాడమీ వారు పోటీ పెట్టేరు. గెలిచిన వారికి సువర్ణ పతకం, 3000 ఫ్రాంకుల నగదు పారితోషికం! మార్చి 1, 1847న ఒక బహిరంగ సభలో పోటీదారులు తమ రుజువుని ఒక నఖచిత్రంలా చూపించవచ్చు. గేబ్రియల్ లమే వేదిక ఎక్కి తాను గత కొన్ని సంవత్సరాలుగా n = 7 అయిన సందర్భాన్ని ఎంత క్షుణ్ణంగా పరిశీలించేడో చెప్పుకుని, రుజువుని ఒక నఖచిత్రంలా చూపించి, పూర్తి ఋజువుని అతి త్వరలో అకాడమీవారి పత్రికలో ప్రచురించబోతున్నానని చెప్పి, వీక్షకులని, శ్రోతలని సంభ్రమాశ్చర్యాలలో ముంచి, తనదే సువర్ణ పతకం అన్న ధీమాతో వేదిక దిగేడు.

వెనువెంటనే సభలో కూర్చున్న ఒక ఆసామీ లేచి తన వద్ద ఉన్న ఋజువుని కూడ పరిశీలించవలసిందిగా కోరేడు. ఆ వ్యక్తి మరెవరో కాదు – ఆయన లుయీ కోషీ (Augustine-Louis Cauchy)! ఈయన ఋజువుకీ లమే ఋజువుకీ పోలికలు లేకపోలేదు. నెల గడిచింది. ఇద్దరూ తమ రుజువులని ప్రచురించేరు. కోషీ పొగరుబోతు. దురహంకారి. అయినా గణిత ప్రపంచం ఆయనని భరించడానికి కారణం ఆయన మేథస్సు. అందుకని అంతా లమే గెలిస్తేనే బాగుంటుందని అనుకుంటున్నారు.

ఎర్న్‌స్ట్ కుమ్మర్ (1810 – 1893)

ఫలితాలు ప్రకటించడానికి సభ ఉత్కంఠ భరితంగా ఉంది. సువర్ణ పతకాన్ని గెలుచుకున్న వ్యక్తి లమే కాదు, కోషీ కాదు. వీరిద్దరి రుజువులు దోషభూయిష్టమే అంటూ జెర్మనీ దేశస్థుడు ఎర్న్‌స్ట్ కుమ్మర్ (Ernest Kummer) రాసిన ఉత్తరం చదివేరు సభాధ్యక్షుడు లుయివిల్. కుమ్మర్ దృష్టిలో ప్రధాన సంఖ్యలు రెండు రకాలు: క్రమ (regular) ప్రధాన సంఖ్యలు, అపక్రమ (irregular) ప్రధాన సంఖ్యలు. లమే, కోషీ ఈ వ్యత్యాసాన్ని గమనించకుండా ఋజువులు చేసేరు. వారి రుజువులు క్రమ ప్రధాన సంఖ్యల యెడల వర్తిస్తాయి కాని అపక్రమ ప్రధాన సంఖ్యల యెడల వర్తించవు. ఈ అపక్రమ ప్రధాన సంఖ్యలు ఒకటీ, రెండునా? అవి కూడ అనంతమైనన్ని ఉన్నాయి. కనుక సోఫీ చూపించిన రుజువునీ, లమే, కోషీల రుజువులని లెక్కలోకి తీసుకున్నా ఇంకా అనంతమైనన్ని సందర్భాలు రుజువు లేకుండా మిగిలిపోతాయి.

కుమ్మర్ దృష్టిలో ఈ సమస్య పరిష్కారానికి కావలసిన పరిపక్వత అప్పటి గణితశాస్త్రానికి లేదు. అనంతంగా ఉన్న ఈ అపక్రమ ప్రధాన సంఖ్యలని ఒక్క పెట్టున సంహరించాలి కాని, ఒకదాన్ని, మరొక దాన్నీ అనుకుంటూ ప్రత్యేక పద్ధతులతో ఎన్నాళ్ళని వేగడం?

ఈ దెబ్బతో ఒక అధ్యాయం ముగిసిందని చెప్పవచ్చు. ఈ సమస్య పరిష్కారానికి మార్గం ఇరవయ్యవ శతాబ్దం వచ్చే వరకూ దొరకలేదు కానీ, ఆ పరిష్కారానికి కావలసిన విత్తులు ఫ్రాన్స్ లోనే, 18వ శతాబ్దంలోనే, పడ్డాయి.

ఇంతవరకు జరిగిన చరిత్రని చెప్పడం అంత కష్టం కాలేదు. ఇటుపైన చెప్పబోయే కథనం క్లిష్టాతి క్లిష్టం! గణితంలో ఉన్నత స్థాయి చదువులు చదివినవారికి కూడ అందుబాటులో ఉండనంత క్లిష్టం! వ్రతం చెడ్డా ఫలం దక్కాలి కనుక ప్రయత్నించి చూస్తాను.

రెండవ భాగం

4. ఇవరీస్ట్ గేల్వా (Evariste Galois)

పేరిస్ నగరానికి దక్షిణాన ఉన్న ఒక చిన్న ఊళ్ళో ఇవరీస్ట్ గేల్వా (Evariste Galois) 23 అక్టోబరు 1811లో పుట్టేడు. అప్పటికి ఫ్రెంచి విప్లవం ముగిసి ఇరవై ఏళ్ళు అయింది. నెపోలియన్ బోనాపార్టే శక్తి యుక్తులు ఉచ్చ దశలో ఉన్న రోజులవి. గర్వమదాంధతతో ఉన్న నెపోలియన్ రష్యా మీదకి దండెత్తేడు. అది బెడిసికొట్టి 1814లో ఎల్బా దీవిలో నిర్బంధించబడ్డాడు. పద్దెనిమిదవ లుయీ (King Louis XVIII) మహరాజు 1815లో సింహాసనాన్ని తిరిగి అధిరోహించిన రోజులవి. ఏడాది తిరిగే లోగా నెపోలియన్ ఎల్బా దీవి లోని బందిఖానా నుండి తప్పించుకుని, లుయీ మహరాజుని సింహాసనం నుండి దింపి రాజ్యం తిరిగి చేజిక్కించుకున్నాడే కాని, నూరు రోజులు తిరగకుండానే బ్రిటన్ యొక్క నావికా దళాధిపతి విల్సన్ చేతుల్లో వాటర్‌లూ దగ్గర పరాజితుడవడంతో పద్దెనిమిదవ లుయీ మళ్ళా పగ్గాలు అందుకున్నాడు.

4.1 బాల్యం

ఇవరీస్ట్ గేల్వా (1811 – 1832)

ఇలా ఒడిదుడుకులతో స్థిరత్వం లేని రాజకీయ వాతావరణంలో ఇవరీస్ట్ గేల్వా పుట్టి పెరిగేడు. మరొక చోట, మరొక సమయంలో పుట్టి ఉంటే కథ మరొక విధంగా పరిణమించి ఉండేదేమో! ఇవరీస్ట్ గేల్వా తల్లిదండ్రులు – అడలైడ్ మరీ గేల్వా, నికలస్ గేబ్రియల్ గేల్వా – కులీన వర్గానికి చెందిన సంపన్న కుటుంబీకులు అవడం ఒకటి, అతని తండ్రి రాజకీయాలలో ముణిగి ఉండడం మరొకటి – ఈ రెండూ చిన్న గేల్వా మనోభావాలని బాగా ప్రభావితం చేసేయి. ఇవరీస్ట్ గేల్వాకి నాలుగేళ్ళ వయస్సప్పుడు, అనగా పద్దెనిమిదవ లూయీ సింహాసనాన్ని తిరిగి అధిరోహించిన కొత్త రోజుల్లో, నికలస్ వారి ఊరికి మేయర్‌గా ఉండేవాడు. రాజపక్షం ప్రభుత్వంలో ఉన్నా ప్రజా (రిపబ్లికన్) పక్షానికి చెందిన నికలస్ మేయర్ పదవిని పోగొట్టుకోకపోవడానికి ముఖ్య కారణం అతను తన కవిత్వపు చమక్కులతో ప్రజాబాహుళ్యంలో సంపాదించుకున్న పరపతే! తల్లి అడలైడ్ జడ్జి కూతురు. సాహిత్యం బాగా చదువుకుంది. ఆ తల్లి పర్యవేక్షణ లోనే గేల్వా ప్రాథమిక విద్య కొనసాగుతూ ఉండేది.

4.2 విద్యాభ్యాసం

అక్టోబరు 1823లో తన పన్నెండవ ఏట, ఇవరీస్ట్ గేల్వా పేరిస్‌లో ఉన్న ప్రతిష్ఠాత్మకమైన, కఠోర క్రమశిక్షణా దక్షుల ఆధ్వర్యంలో నడుస్తూన్న, ప్రభుత్వ రంగపు ఉన్నత పాఠశాలలో ప్రశాంతత లేని పరిస్థితులలో చేరేడు. మొదటి ఏట అతనికి గణితం అధ్యయనం చేసే అవకాశం రాలేదు. మిగిలిన పాఠ్యాంశాలలో బొటాబొటీ ప్రతిభతో నెట్టుకు వస్తున్నాడు. ఈ లోగా, పులి మీద పుట్రలా, పాఠశాల పాలకవర్గంలో మార్పు వచ్చింది. పూర్వపు రోజులలో నడిపిన క్రైస్తవ ఫాదరీల ఆధ్వర్యంలోకి ఈ పాఠశాల తిరిగి రావడంతో పాఠశాల అధికార వర్గం రాజపక్షం వైపు మొగ్గు చూపించడం మొదలు పెట్టింది. అప్పుడప్పుడే స్వేచ్ఛావాయువులు పీల్చుకుంటూన్న విద్యార్థులకి పురోహిత-పాలక వర్గాల మధ్య తరతరాలుగా వస్తూన్న ఈ దోస్తీ నచ్చలేదు. విద్యార్థి బృందం తిరుగుబాటు చేసి, అల్లర్లు చెయ్యడానికి పన్నాగాలు పన్నుతున్నారు. విద్యార్థుల కుట్ర వెనక ప్రజాపక్షం మద్దత్తు ఉందని పసిగట్టిన పాఠశాల కులపతి విద్యార్థి బృందపు నాయకులలో పదిమందిని పాఠశాల ప్రాంగణం నుండి – క్రమశిక్షణ రక్షణార్థం – బహిష్కరించేరు. అలా బహిష్కరించి, మిగిలిన విద్యార్థులందరిచేత ఫ్రాన్స్ రాజుని, జెండాని గౌరవించి క్రమశిక్షణతో మసులుకుంటామనిన్నీ, అలా కానియెడల వారిని దేశద్రోహులుగా పరిగణించి శిక్షించవచ్చనిన్నీ ప్రమాణం చెయ్యమని ఆదేశించేడు. అలా ప్రమాణం చెయ్యడానికి నిరాకరించిన వందమంది విద్యార్థులని బందిఖానాలో పడేసేరు. ఈ సంఘటనలు వేటిల్లోనూ గేల్వా పాల్గొనలేదు కాని, ఇవి అతని లేత మనస్సుని బాగా ప్రభావితం చేసేయి. ప్రభుత్వ హస్తం చేస్తూన్న దండ ప్రయోగం అతనికి నచ్చలేదు. తండ్రి మక్కువ చూపిన ప్రజాపక్షం వైపే అతనూ మొగ్గడం మొదలు పెట్టేడు.

4.3 గణితంతో పరిచయం

గేల్వాకి పదహారు సంవత్సరాలు వచ్చే వరకు గణితం అధ్యయనం చేసే అవకాశం రాలేదు. గణితం ఒక సారి చవి చూసిన తరువాత అతనికి మరే ఇతర అధ్యయనాంశం మీదకి మనన్సు పోలేదు. కన్ను మూసినా, కన్ను తెరచినా గణితమే! మరొక ధ్యాస లేదు. ‘ఇది గణితోన్మాదం! ఇతని గణితం గురువులకే పట్టుబడడం లేదు. మిగిలిన పాఠ్యాంశాలని చదవమని ఇతనిని నిర్బంధించడం వల్ల గురువులని యాతన పెట్టడం, గురువులు ఇతనిని శిక్షించడం తప్ప సాధించగలిగేది ఏదీ ఉండదు.’ అంటూ అధికారులు అతని వార్షిక పురోగమన నివేదికలో నమోదు చేసేరు.

ప్రత్యక్షంగా ఉన్న గురువుల దగ్గర నేర్చుకునేది ఏదీ లేక, ఏకలవ్యుడిలా, ప్రపంచ ప్రఖ్యాతి పొందిన గణిత శాస్త్ర వేత్తలు రాసిన పరిశోధనా పత్రాలు, పుస్తకాలు ఆవురావురుమంటూ కబళించడం మొదలు పెట్టేడు, గేల్వా. పదిహేడేళ్ళు నిండేసరికి తన ప్రప్రథమ పరిశోధనా పత్రాన్ని ఒక ప్రతిష్ఠాత్మకమైన పత్రికలో ప్రచురించేడు. శేష జీవితం వడ్డించిన విస్తరిలా ఉండవలసినదే కాని ఈ ఉత్పాతపిండపు మేథస్సే ఇతని పతనానికి కారణం అవడం విచారించవలసిన విషయం. ఇతను ఆవిష్కరిస్తున్న గణితం ఎవ్వరికీ అర్థం అయేది కాదు. ఇతరులకి అర్థం అయే రీతిలో విడమరచి ఒక క్రమ పద్ధతిలో చెప్పే నేర్పు, ఓరిమి గేల్వాకి ఉండేవి కావు. అందుచేత ఇతని మేథో ఉత్పత్తి అంతా అడవి కాసిన వెన్నెల అయిపోయేది. తత్కారణంగా క్రమం తప్పకుండా పరీక్షలు అన్నీ తప్పేవాడు.

ఫ్రాన్స్ దేశంలోనే అతి ప్రతిష్ఠాత్మకమైన విశ్వవిద్యాలయం ఇకోల్ పోలీటెక్నిక్‌లో ప్రవేశార్హత కోసం దరఖాస్తు పడేసేడు. అక్కడకి వెళ్ళి చదువుకోవాలనే కోరికకి ప్రేరణ కారణం ప్రతిభావంతులైన గురువుల దగ్గర నేర్చుకోవాలనే అభిలాష కాదు; ఇకోల్ పోలీటెక్నిక్ ప్రజా పార్టీ రాజకీయాలకి ఆటపట్టని! ఎప్పటిలాగే ప్రవేశ పరీక్షలలో దుడుకుతనం, పరీక్షాధికారులు అడిగే ప్రశ్నలకి నమ్రతతో సమాధానం చెప్పే ఓరిమి లేక పోవడంతో గేల్వాకి ప్రవేశం నిరాకరించేరు. మరుసటి సంవత్సరం మళ్ళా ప్రయత్నించేడు. ఈ సారి పరీక్ష చేసే అధికారికి తను నల్లబల్ల మీద రాస్తున్న గణితం అర్థం కాకపోయేసరికి చిరాకుతో చేతిలో ఉన్న డస్టరు ఆయన మీదకి విసరి కొట్టేడు. అధికారికి ముఖం మీద దెబ్బ తగిలింది. పరీక్ష అంతటితో ఆగిపోయింది. ఇకోల్ పోలీటెక్నిక్‌లో ప్రవేశం పొందే అర్హత శాశ్వతంగా పోగొట్టుకున్నాడు.

4.5. గేల్వా ప్రతిభ

ఇంతకీ గేల్వా గణితంలో ప్రతిభ ఎక్కడ చూపించేడో చెప్పనే లేదు కదూ. గేల్వా గణిత సమీకరణాలని పరిష్కరించడంలో అసమానమైన ప్రతిభ చూపించేవాడు. చదువరులలో చాల మంది, ఉన్నత పాఠశాలలో, బీజగణితం నేర్చుకున్నప్పుడు వర్గ సమీకరణాలని పరిష్కరించడం నేర్చుకునే ఉంటారు. వర్గ సమీకరణం చూడడానికి ఈ దిగువ చూపిన విధంగా ఉంటుంది:

ax² + bx + c = 0

ఇక్కడ a, b, c అనేవి ఏ విలువ అయినా తీసుకోవచ్చు. వీటికి ఏవో ఫలానా విలువలు అంటూ ఆపాదించిన తరువాత, x కి ఏ విలువ ఇస్తే పైన ఇచ్చిన సమీకరణం చెల్లుతుంది? ఉన్నత పాఠశాలలో దీనిని పరిష్కరించే సూత్రం పిల్లలకి కంఠతా వచ్చేస్తుంది: ఎక్స్ ఈజ్ ఈక్వల్ టు మైనస్ బి, ప్లస్ ఆర్ మైనస్ రూట్ ఆఫ్ బి స్క్వేర్ మైనస్ ఫోర్ ఎ సి హోల్ డివైడెడ్ బై టు ఎ.

x = (-b +/- √b² – 4ac)/2a

ఉదాహరణకి పై సమీకరణంలో a =2, b = -6, c = 4 అయిన పక్షంలో x విలువ 1 కాని 2 కాని అయితే సమీకరణం చెల్లుతుంది. ఇటువంటి వర్గ సమీకరణాలని (లేదా ద్విఘాత సమీకరణాలని) పరిష్కరించడం నల్లేరు మీద బండి నడక.

వీటి కంటె మరికొంచెం క్లిష్టమైనవి త్రిఘాత సమీకరణాలు. వీటికి ఉదాహరణ:

ax³ + b x² + c x + d = 0

మరొక మెట్టు పైకి వెళితే చతుర్ఘాత సమీకరణాలు వస్తాయి.

ax⁴ + b x³ + c x² + d x + e = 0

ఈ రెండు రకాల సమీకరణాలని పరిష్కరించే మార్గాలు – తేలిక కాదు కానీ – 19 వ శతాబ్దంలోనే కనుక్కున్నారు. కాని పంచఘాత సమీకరణాలు,

ax⁵ + b x⁴ + c x³ + d x² + e x + f = 0

ఎవ్వరికీ కొరుకుబడ లేదు. ఈ సమీకరణాన్ని పరిష్కరించి తీరాలనే కోరిక గేల్వా మెదడులో దూరి కుమ్మరి పురుగులా గొలకడం మొదలు పెట్టింది. పదిహేడు ఏళ్ళు నిండక ముందే దీని పరిష్కార మార్గం సుగమం చేస్తూ రెండు పరిశోధనా పత్రాలు రాసి, ప్రచురణకి పరిశీలించవలసిందిగా కోరుతూ, శాస్త్రీయ అకాడమీ వారికి, అనగా ఫ్రాన్సులో ఆనాటి ఘనాపాటీ అయిన అగస్టిన్ కోషీకి పంపేడు. ఈ కుర్రాడి ప్రతిభకి చకితుడైన కోషీ, అకాడమీవారు ఇచ్చే అగ్ర బహుమానానికి అర్హత పొందాలంటే రెండు పరిశోధనా పత్రాలనీ ఒకటిగా చేసి తిరగ రాసి పంపాలని సూచన చేసి తిరిగి పంపేడు.

4.6 గేల్వాకి జరిగిన అన్యాయం

గేల్వా ఆనందానికి అవధులు లేవు. ఇకోల్ పోలీటెక్నిక్ వారు ప్రవేశం నిరాకరిస్తేనేమి, గణిత ప్రపంచం తన ప్రతిభకి పట్టం కట్టబోతూంది. కాని అదేమి ప్రారబ్దమో కాని అటు తరువాత మూడేళ్ళపాటు పడరాని కష్టాలు పడ్డాడు. అందులో స్వయంకృతాపరాధం కొంత. జులై 1829లో గేల్వా చదువుతూన్న పాఠశాలకి రోమన్ కేథలిక్ చర్చి నియమించిన ఒక కొత్త ఫాదర్ కులపతిగా వచ్చేడు. ఆయనకి గేల్వా తండ్రి నికలస్ యొక్క ఉదార భావాలతో కూడిన ప్రజాపార్టీ పేరు చెబితే చాలు ఒళ్ళు మండేది. ఆ దుగ్ధతో ఆయన నికలస్ పరువు ప్రతిష్ఠ మంటగలిసేలా ఒక పన్నాగం పన్నేడు: ఊళ్ళో పెద్దలని, మర్యాదస్తులని ఉద్దేశించి బూతు పద్యాలు రాసి, నికలస్ పేరు మీద ఆయనే ప్రచురించడం మొదలు పెట్టేడు. బహిరంగంగా జరిగిన ఈ పరాభవం భరించలేక నికలస్ ఆత్మహత్య చేసుకున్నాడు.

తండ్రి శరీరాన్ని ఖననం చేసే సందర్భంలో కొత్తగా వచ్చిన కులపతి చేసిన కుట్ర బయట పడింది. శ్మశానంలో ఇరు పక్షాల వారి మధ్య పెద్ద దొమ్మీ జరిగింది. ఆ దొమ్మీలో నికలస్ శరీరం ఉన్న శవపేటిక అపసవ్యంగా జారి గోతిలో తిరగబడి పోయింది. ప్రభుత్వం కనుసన్నలలో తండ్రికి జరుగుతున్న పరాభవం భరించలేక గేల్వా మనస్సు ప్రతీకార జ్వాలతో ప్రజ్వరిల్లింది.

పేరిస్ తిరిగి వచ్చి, దుఃఖాన్ని దిగమింగుకుని, కోషీ చెప్పిన విధంగా తన పరిశోధనా పత్రాలు రెండింటిని ఒకటిగా తిరగ రాసి, కోషీ ఆదేశానుసారం ఆ పత్రాన్ని అకాడమీ కార్యదర్శి అయిన జోసెఫ్ ఫురియేకి (Joseph Fourier) పంపేడు. పధ్ధతి ప్రకారం అది ఆయన నిర్ణాయకులకి పంపాలి. గేల్వా పత్రం పంచఘాత సమీకరణాలని పరిష్కరించే మార్గం చూపలేదు కాని ఆ సమీకరణాల అంతర్గత లక్షణాలని నిశితంగా పరిశీలించడానికి అవసరమైన సూక్ష్మేక్షికని (insight) ఇచ్చింది. ఆ సూక్ష్మాక్షిక పరిశీలనకే ముగ్ధుడైన కోషీ పత్రాన్ని పోటీకి పంపమని ప్రోద్బలపరచేడు.

పోటీ ఫలితాలు ప్రకటించేరు. గేల్వాకి బహుమతి రాకపోవడమే కాదు, గేల్వా రాసిన పత్రం పోటీలోకి ఎక్కనే లేదు! పోటీ ఫలితాలు మరొక రెండు వారాలలో ప్రచురిస్తారనగా ఫురియే మరణించేడు. గేల్వా పత్రం ఆయన పోటీకి పంపలేదా? పంపితే అక్కడ గిట్టని వాళ్ళు ఈ పత్రాన్ని పోటీ నుండి తప్పించేరా? ఎక్కడో, ఎవ్వరో గూడుపుఠాణీ చేసేరు. గేల్వా దఖలు చేసుకున్న పత్రం మళ్ళా ఎవ్వరికీ ఎక్కడా కనిపించలేదు. గేల్వాకి జరిగిన ఈ ఘోరమైన అన్యాయాన్ని ఒక పాత్రికేయుడు ఇలా రాసేడు:

“గత సంవత్సరం, మార్చి 1వ తేదీకి ముందు, గేల్వా పోటీలో పాల్గొనే నిమిత్తం అకాడమీ కార్యదర్శికి ఒక పరిశోధనా పత్రం సమర్పించడం జరిగింది. ఆ పత్రంలో బహుపద సమీకరణాలని పరిష్కరించే సందర్భంలో ఎదురయే సమస్యలు, పరిష్కార మార్గాలు క్రొత్త కోణంలో ముచ్చటించబడ్డాయి. అకాడమీ వారు గణితంలో ఏటేటా ఇచ్చే బృహత్ బహుమానానికి జరిగే పోటీలో ఈ పత్రం అభ్యర్థిగా ఉండవలసింది. అంతే కాదు. లగ్రాంజ్ సాధించలేకపోయిన సమస్యని పరిష్కరించింది కనుక ఈ పత్రానికే ఆ బహుమానం రావలసింది. అంతే కాదు. కోషీ ఈ కుర్రాడు చేసిన పనిని మార్గదర్శినిగా కొనియాడి పోటీకి పంపమని స్వయంగా ప్రోత్సహించేరు. చివరికి ఏమయింది? గేల్వా రాసిన పరిశోధనా పత్రం అయిపు లేకుండా మాయం అయిపోయింది. బహుమానం దక్కవలసినవారికి దక్కలేదు.” – గ్లోబ్, 1831.

ఇది ఎవ్వరో చెయ్యాలని చేసిన కుట్ర అవాలి తప్ప దఖలు పరచిన పరిశోధనా పత్రం ఫికరు లేకుండా పోవడం ఏమిటి? అనుకున్నాడు గేల్వా. ఈ అనుమానాన్ని బలపరుస్తూ మరొక సంఘటన జరిగింది. గేల్వా తరువాత రాసిన మరొక పరిశోధనా పత్రాన్ని అకాడమీ ప్రచురించడానికి నిరాకరిస్తూ -దీని పటిష్ఠత నిర్ణయించడానికి కావలసిన పరిపక్వత, తార్కిక హంగులు ఇందులో లేవు, అంటూ వ్యాఖ్యానించింది. గణిత ప్రపంచపు సరిహద్దులలోకి కూడా అకాడమీ వారు తనని రానివ్వరని గేల్వాకి స్పష్టం అయిపోయింది. ప్రజా పార్టీ తరఫున పోరాడి ప్రభుత్వం తనకి చేసిన అన్యాయానికి ప్రతీకారం తీర్చుకోవాలనే నిశ్చయానికి వచ్చేడు.

ప్రతిష్ఠాత్మకమైన ఇకోల్ పోలీటెక్నిక్‌లో తనకి ప్రవేశం దొరకనందున అంతకంటె ఒక్క వాసి తక్కువ అయిన ఇకోల్ నార్మాల్‌లో విద్యార్థిగా ఉన్న గేల్వా చదువుకి స్వస్తి చెప్పేసి విద్యార్థి రాజకీయాలలో ప్రవేశించేడు. రాజపక్షం వాళ్ళు, ప్రజాపక్షం వాళ్ళు పేరిస్ వీధులలో ముష్టి యుద్ధాలు చేసుకుంటున్న రోజులవి. రాజపక్షం వాడైన ఇకోల్ నార్మాల్ కులపతి ప్రజాపక్షం తరఫున పోరాడుతున్న విద్యార్థులని హాస్టలు దాటి బయటకి పోకుండా పాఠశాల ప్రాంగణానికి ఉన్న గేటు తలుపులు మూయించేడు. తన అనుయాయులతో పోరాడడానికి వీలు లేకుండా ప్రతిబంధకాలు ఏర్పరచిన ఆ కులపతిపై ఆగ్రహంతో విరుచుకు పడి, దుమ్మెత్తి పోస్తూ వార్తా పత్రికలో ఒక వ్యాసం ప్రచురించేడు, గేల్వా. కులపతి దమ్ములు లేని పిరికి పంద అన్నాడు. కులపతికి కోపం కమ్ముకొచ్చి వినయ విధేయతలు చూపని గేల్వాని శాశ్వతంగా పాఠశాల నుండి బహిష్కరించేడు. దీనితో గేల్వాకి విద్యా సంస్థల తోటీ, తద్వారా గణితశాస్త్రపు ప్రపంచం తోటీ ఋణం తీరిపోయింది.

4.7 రాజకీయాలలో ప్రవేశం

ఇలా పోరాడలేక గేల్వా ప్రజాపార్టీ వారి స్వతంత్ర సైన్యంలో సైనికుడిగా చేరేడు. నెల తిరిగే లోగా కొత్తగా సింహాసనం అధిష్టించిన లుయీ-ఫిలిప్ దేశంలో ప్రబలుతున్న అరాజకాన్ని అరికట్టడానికి అజాదీ దళాన్ని రద్దు చేస్తూ దానికి చట్టపరమైన ఉనికి లేదని ఉత్తర్వు జారీ చేసేడు.

గేల్వా తండ్రిని పోగొట్టుకున్నాడు. పాఠశాలలో తన స్థావరాన్ని పోగొట్టుకున్నాడు. గణిత ప్రపంచంలో అతని పనికి గుర్తింపు లేకుండా పోయింది. చివరికి అతను దేశం కోసం పోరాడతానంటూ చేరిన సైన్యం చట్టవిరుద్ధం అని బహిష్కరణ పొందింది. ఫ్రాన్స్ దేశంలోనే అతి మేథావంతుడనదగ్గ కుర్రాడు ప్రభుత్వపు ప్రబల శక్తులకి బలి అయిపోతున్నాడనే తపనతో అప్పటికే వయసు మళ్ళుతూన్న సోఫీ జెర్మైన్ ఇలా వాపోయింది: “గణిత ప్రపంచానికి దుర్దశ పట్టినట్లుంది. ఫురియే మరణంతో సుడిగుండాలలో పడి ములిగిపోతూన్న గేల్వాకి కనీసం గడ్డిపోచ లాంటి ఆసరా కూడ లేకుండా పోయింది. పాఠశాలలో స్థావరం లేదు. తండ్రి లేడు. తల్లి ఉంది కాని ఆమె దగ్గర ఇహ ఏమీ లేదు. ఎదుటివారి మీద గౌరవం చూపకుండా దూకుడుతనం చూపే ఇతని స్వభావం మారలేదు. ఈ కుర్రాడికి పిచ్చో, వెర్రో ఎక్కిపోతుందని అంటున్నారు. అది మూడొంతులు నిజమే కావచ్చు.”

గేల్వా రాజకీయాలలో తలదూర్చుతూన్నంత సేపూ అతని జీవితానికి నిష్కృతి లేదేమో! ఆనాటి మేటి రచయిత అలెగ్జాండర్ డూమా (Alexander Dumas) ఒక ఫలహారశాలలో ఒక పరిచయస్తునితో మాట్లాడుతూ ఉన్న సమయంలో అతని కనుసన్నలలో కనిపించిన ఒక సంఘటనని ఇలా వర్ణించేడు: “నా పక్క నుండి లూయీ-ఫిలిప్ పేరు వినిపించింది. వెనువెంటనే ఎవ్వరో నాలుగైదు సార్లు ఊళ వేసేరు. ఆ శబ్దం వచ్చిన వైపు తల తిప్పి చూసేను. అల్లంత దూరంలో, ఏదో కోలాహలం మధ్య గల్లంతు జరుగుతోంది. ప్రభుత్వం అంటే ఇంతకంటె ఎక్కువ వైరభావం ఉన్న మరో రెండు వందల మంది పేరిస్‌లో మరెక్కడా కనిపించరేమో! ఒక కుర్రాడి చేతిలో ఒక కత్తి, మరొక చేతిలో మాదక ద్రవ్యమో మరేదో ఉన్న గ్లాసు. అతను రెండు చేతులూ పైకెత్తి అరుస్తున్నాడు. అతను ప్రజా పార్టీకి చెందిన ఇవరీస్ట్ గేల్వా! “అయ్యలారా! అమ్మలారా! …” అంటూ ఏమంటున్నాడో ఆ కోలాహలంలో సరిగ్గా వినిపించలేదు. లూయీ-ఫిలిప్‌ని ఎవ్వరో బెదిరిస్తున్నట్లు నాకు వినపడింది. గేల్వా మాత్రం ఒర లోంచి కత్తిని తీసి ఝళిపించడం మాత్రం స్పష్టంగా కనిపించింది. నేనూ ప్రజాపార్టీ అంటే సానుభూతి ఉన్నవాడినే. కాని ఈ ఝళిపింపు, బెదిరింపు శ్రుతి మించినట్లనిపించింది. నాతో మాట్లాడుతున్న వ్యక్తి రాజుగారి ఆస్థానంలో విదూషకుడు. అతని కళ్ళు ఎర్రబడ్డాయి. కోపంతో ముందుకి దూకేడు. దీని పర్యవసానం బాగుండదనే భావనతో నేను అక్కడనుండి తప్పుకున్నాను. రెండు రోజులలో ఇవరీస్ట్ గేల్వాని నిర్బంధించేరన్న వార్త విన్నాను.”

4.8 గేల్వాపై కుట్ర

బందిఖానాలో నెల్లాళ్ళు ఉంచిన తరువాత రాజు లుయీ-ఫిలిప్‌ని హత్య చెయ్యడానికి ప్రయత్నించేడన్న నేరం మోపి గేల్వాని న్యాయస్థానానికి ఈడ్చుకు వచ్చేరు. ఫలహారశాల వద్ద జరిగిన గలాటాలో ఎవ్వరి మాటా ఎవ్వరికీ సరిగ్గా వినబడనందున ఆ బెదిరింపు మాటలు గేల్వా అన్నవో, మరెవ్వరో అన్నవో అన్నది అనుమానానికి అవకాశం లేకుండా న్యాయస్థానం నిర్ధారించలేకపోయింది. ఇరవై ఏళ్ళయినా నిండని కుర్రాడి మీద కొంత కనికరం చూపించి న్యాయస్థానం కుర్రాడి మీద వచ్చిన అభియోగాన్ని తోసి పుచ్చి అతనిని విడుదల చేసింది.

జులై 14, 1831. బేస్టీల్ డే – ఫ్రెంచి వారి జాతీయ దినోత్సవం. ఫ్రెంచి విప్లవంలో రాచరికాన్ని కూలదోసిన ప్రజాస్వామ్యశక్తులు జరుపుకునే ఉత్సవం. నిషేధించబడ్డ స్వతంత్ర సైన్యపు సైనిక దుస్తులు వేసుకుని ఇవరీస్ట్ గేల్వా పేరిస్ నగరం వీధుల వెంట కవాతు చేస్తూ నడవడం మొదలు పెట్టేడు. ఇతను ప్రభుత్వాన్ని ఎద్దేవా చేద్దామని చేసిన పనే ఇది. ప్రభుత్వం వెంటనే అతనిని నిర్బంధించింది.

వారం రోజులు పోయిన తరువాత గదిలో ఉన్న ఖైదీ మీద తుపాకీ గురి పెట్టి ఎవ్వరో పేల్చేరు. అది గురి తప్పి పక్కనున్న ఖైదీకి తగిలింది. ఆ తూటా తనకొరకే నిర్దేశించబడిందని గేల్వా నమ్మేడు. అతని మేథని ఒక రకం మనోవ్యాకులత ఆవరించింది. తాగుడుకి దాసుడయాడు. ఆత్మహత్య చేసుకుందుకి ప్రయత్నించేడు. తోటి ఖైదీలు ఆపి ప్రాణం కాపాడేరు.

మార్చి 1832లో, ఇంకొక నెలలో గేల్వా నిర్బంధం పూర్తయి విడుదల అవుతాడనగా, పేరిస్‌లో కలరా విరుచుకు పడడంతో ఖైదీలందరినీ విడుదల చేసేరు. ఆ తరువాత కొన్ని వారాల పాటు గేల్వా మృత్యువు వాత పడ్డాడో, మరేమయ్యాడో ఎవ్వరికీ తెలియలేదు. కాని అభిజ్ఞ వర్గాలలో అనుకున్నది ఏమంటే స్టెఫనీ అనే అమ్మాయితో ప్రేమలో పడ్డాడని. ఈ అమ్మాయి ఒక వైద్యుడి కూతురు. వీరిద్దరికీ పరిచయం ఎప్పుడయిందో, అది ప్రేమగా ఎప్పుడు పరిణమించిందో తెలియదు కాని ఈ ప్రేమ కలాపపు విషాదాంతం మాత్రం పొల్లు పోకుండా చరిత్రకారులు భద్రపరిచేరు.

పేరిస్‌లో కులీన వర్గానికి చెందిన పేషో డెర్బిన్విల్ అనే వ్యక్తీ ఈ స్టెఫనీని అంతకు ముందే ప్రేమించేడుట. ఈమె గేల్వాతో తిరుగుతున్నదని డెర్బిన్విల్ పసిగట్టి ఉగ్రుడయాడుట. స్నేహితురాలిని ఏమీ చెయ్యలేక గేల్వా మీద కత్తిగట్టి కాలు దువ్వేడు. స్టెఫనీ కావాలంటే తనతో ద్వంద్వ యుద్ధం చేసి గెలుచుకోమన్నాడు. గేల్వాకి ఒక్క రాత్రి మాత్రమే గడువిచ్చాడు. డెర్బిన్విల్‌తో ద్వంద్వ యుద్ధంలో తను గెలవలేడని గేల్వాకి తెలుసు. అయినా ఈ యుద్ధానికి ఎందుకు ఒప్పుకున్నాడో మనకి తెలియదు.

గేల్వా కాగితం

ప్రజాపక్షం మీద ఎంత అభిమానం ఉన్నా, స్టెఫనీ మీద ఎంత ప్రేమ ఉన్నా అవి గేల్వాకి గణితం మీద ఉండే పిచ్చి ప్రేమతో సరి తూగలేకపోయాయి. అకాడమీ వారి మన్ననలు పొందలేకపోయిన అతని పరిశోధనా ఫలితాలు గణిత ప్రపంచానికి తెలియకుండా కాలగర్భంలో కలిసిపోకూడదని అనుకున్నాడు. ఆ రాత్రంతా మేలుకుని తను ఆవిష్కరించిన గణిత సిద్ధాంతాలన్నిటిని కాగితాల మీద బరబరా గీకడం మొదలు పెట్టేడు.

ఇవన్నీ తను కోషీకి, తరువాత ఫురియేకి పంపిన పరిశోధనా పత్రాలలోని సిద్ధాంతాలు, వాటి రుజువులు! అసలే సిద్ధాంతాలు, రుజువులు ఒక క్రమ పద్ధతిలో రాసే అలవాటు, ఓపిక లేని వాడు. దానికి తోడు మరునాడు మరణం తథ్యం అని నమ్మిన మనిషి. దానితో మనస్సుకి నిలకడ లేక రాసిన రాత అంతా కొక్కిరిబిక్కిరిగా రాసేడు. ఆ కొక్కిరిబిక్కిరి రాతల మధ్య నిశిత దృష్టితో పరిశీలించిన వారికి స్ఠెఫనీ ప్రస్తావన కూడ కనిపించింది. తెల్లారిపోతోంది. ద్వంద్వ యుద్ధానికి సమయం ఆసన్నమవుతోంది. ఇంకా రాయవలసిన గణితం చాల ఉంది. కాని ‘వేళ సరిపోలేదు’ అంటూ అర్థాంతరంగా వాక్యాన్ని మధ్యలో ఆపేసి, ఆ కాగితాలన్నిటిని కట్టగట్టి తన స్నేహితుడు అగస్ట్ షెవాలియేకి పంపి, తను కాని మరునాటి ద్వంద్వ యుద్ధంలో కాని చనిపోతే ఆ కాగితాలకి నకళ్ళు తీసి యూరప్‌లో ఉన్న ప్రతిష్ఠాత్మకమైన గణిత శాస్త్రవేత్తలందరికీ పంపమంటూ ఇలా వేడుకున్నాడు:

ప్రియ మిత్రమా:

గణితశాస్త్రంలో నేను కొన్ని సరికొత్త ఫలితాలు సాధించేను. వీటిలో మొదటిది పంచఘాత సమీకరణాల గురించి, వాటి మూలల (roots) గురించి. ఈ సమీకరణాలు ఏయే సందర్భాలలో పరిష్కారానికి లొంగుతాయో, వాటిని వర్గమూలాలు (radicals) ఉపయోగించి ఎలా నిర్మించవచ్చో, పరిశోధించి కనుక్కున్నాను. వివరాలన్నీ ఈ జాబుతో జత చేసిన పత్రాలలో ఉన్నాయి.

నా జీవితంలో ఎన్నో సార్లు నాకే నమ్మకం లేని ప్రతిపాదనలు ఎన్నో చేసేను. కాని ఈ కాగితాల కట్టలో నేను రాసిన ప్రతిపాదనలు, రుజువులు, అన్నీ నా మనోఫలకం మీద స్పష్టంగా ఉన్నాయి. రుజువులు లేని సిద్ధాంతాలు ప్రతిపాదిస్తే నా పరువు ప్రతిష్ఠలే కదా నష్టపోయేది.

నా తరఫున బహిరంగంగా జకోబీని గౌస్ ని వారి వారి అభిప్రాయాలు వెల్లడించమని అర్థించు. ఎప్పటికో ఒకప్పటికి ఎవ్వరో ఒకరు ఈ సిద్ధాంతాల విలువని గుర్తించకపోరు.

నిన్ను మనస్పూర్తిగా ఆలింగనం చేసుకుంటూ…

— నీ ఇ. గేల్వా

మరునాడు, 30 మే 1832న ఒక మైదానంలో గేల్వా, డెర్బిన్విల్ ఒకరికొకరు ఎదురయేరు – తుపాకిలు చేత పుచ్చుకుని. గేల్వా ఏకాంతంగా నిలబడ్డాడు. డెర్బిన్విల్ సహచరులతో వచ్చేడు.

డెర్బిన్విల్ గురి చూసి కొట్టడంలో ప్రావీణ్యుడు, అనుభవజ్ఞుడు. గేల్వా తుపాకి పైకెత్తి గురి పెట్టి సిద్ధమయే లోగానే డెర్బిన్విల్ మొదటి తూటాకే గేల్వా నేల కూలిపోయాడు. గణిత ప్రపంచం నుండి ఒక తార రాలిపోయింది. క్షతగాత్రుడై నేల కూలిన గేల్వా అసహాయంగా అలా పడి ఉన్నాడు. పొట్ట నుండి రక్తం కారుతూ కొన ఊపిరితో నేల మీద పడున్న గేల్వాని కనీసం కన్నెత్తి అయినా చూడకుండా, డెర్బిన్విల్ తన అనుయాయులతో అక్కడ నుండి నిష్క్రమించేడు. కొన్ని గంటలు పోయిన తరువాత – ద్వంద్వ యుద్ధం గురించి విన్న సోదరుడు – ఆల్ఫ్రెడ్ వచ్చి గేల్వాని కొచిన్ ఆసుపత్రికి (పేరిస్ లోని పెద్ద ధర్మాసుపత్రి) తరలించుకు పోయేడు. మరునాడు గేల్వా దివంగతుడయాడు.

4.9 అంత్యక్రియలు, అన్వీక్షణ

గేల్వా అంత్యక్రియలు అతని తండ్రి అంత్యక్రియలని జ్ఞప్తికి తెచ్చేయి. ప్రజాపక్షపు సభ్యులు, గేల్వా స్నేహబృందం అలజడి చేస్తారన్న భయంతో పోలీసులు ముందు రోజే ముప్ఫయ్ మంది స్నేహితులని ఆపి, అటకాయించి, బందిఖానాలో పడేసేరు. ఈ పని అగ్గిలో ఆజ్యం పోసినట్లయింది. గేల్వా అంత్య క్రియలకి రెండు వేల మంది ప్రజాపక్షపు సభ్యులు హాజరయారు. అక్కడ కాచుక్కూచున్న పోలీసులకి, వీరికి మధ్య పెద్ద గలాటా జరిగింది.

గేల్వా మరణం వెనక పెద్ద గూడుపుఠానీ ఉందని అక్కడ చేరిన దుఃఖితుల నమ్మకం. నిజానికి డెర్బిన్విల్ భగ్న ప్రేమికుడు కాదనిన్నీ, ప్రభుత్వం తరఫున పని చేస్తూన్న గూఢచారి అనీ, స్టెఫనీ ఇతని ప్రేమికురాలు కాదనీ, ఆమె కేవలం ఒక బజారు మనిషనీ ఒక సిద్ధాంతం చలామణీలోకి వచ్చింది. గేల్వా మరణం వెనక ఏదో కుట్ర ఉందనడానికి అతను ఖైదులో ఉన్న రోజులలో అతని కోసం వేసిన తూటాయే పక్కవాడికి తగిలిందని ఒక ఆధారం చూపించడం మొదలు పెట్టేరు. కొంతమంది చరిత్రకారులు ప్రతిపాదించిన సిద్ధాంతం ప్రకారం ద్వంద్వ యుద్ధం కూడ ప్రభుత్వం వారి కుట్రలో ఒక భాగమే!

గేల్వా వదలిపెట్టిన పరిశోధనా పత్రాలని అతని స్నేహితుడు ఓపికగా, మంచి దస్తూరితో తిరగ రాసి, గేల్వా కోరిక ప్రకారం గౌస్, జకోబీ, తదితరులకి ప్రతులు పంపేడు. ఆ పత్రాలు క్షేమంగా గమ్యం చేరుకున్నట్లు కనీసం ఒక్క జాబైనా తిరిగి రాలేదు. ఇలా ఒక దశాబ్దం గడచి పోయింది. అందరూ గేల్వాని మరచి పోయేరు.

గేల్వా సురక్షితంగా కాలగర్భంలో కలిసిపోయాడనుకుంటూన్న తరుణంలో గేల్వా కాగితాలు 1846లో, జోసెఫ్ లుయివిల్ ఒళ్ళో వచ్చి పడ్డాయి. ఆ కాగితాల్లో లుయివిల్ కళ్ళకి ఒక మేథో విస్ఫులింగం కనిపించింది. నెలల తరబడి వాటిని అధ్యయనం చేసి, వాటిని అర్థం చేసుకుని, గణితాన్ని శుభ్రం చేసి, తన సంపాదకత్వంలో నడుస్తూన్న Journal de Mathematiques Pures et Appliquesలో ప్రచురించేడు. ఆ పత్రాలకి గణిత ప్రపంచం నుండి వచ్చిన స్పందన తక్షణికం, అనూహ్యం. పంచఘాత సమీకరణాల పరిష్కారానికి ఒక సమగ్రమైన సిద్ధాంతం అది. ముందు పంచఘాత సమీకరణాలని రెండు వర్గాలుగా విడగొట్టేడు: పరిష్కారానికి లొంగేవి ఒక వర్గం, లొంగనివి రెండవ వర్గం. లొంగేవాటిని పరిష్కరించడానికి ఒక సూత్రం ఇచ్చేడు. ఈ సూత్రంతో షష్ఠ ఘాత, అష్ట ఘాత, వగైరా లన్నిటిని ఎలా ఎదుర్కోవాలో సూచించేడు. పందొమ్మిదవ శతాబ్దపు గణితంలో ఇది అగ్రశ్రేణిలో నిలవదగ్గ గణితశిల్పం.

ఈ పరిశోధనా పత్రాలకి పీఠిక రాస్తూ, లుయివిల్ ఇలా అంటాడు: “గేల్వాలో ఉన్న పెద్ద లోపం క్లుప్తత కోసం పాటుపడడం. అమూర్త బీజగణితం (abstract algebra) వంటి వస్తువుని తీసుకున్నప్పుడు క్లుప్తత కంటె స్పష్టతకి, సుబోధకతకి పెద్ద పీట వెయ్యాలి. సుగమంగా లేని క్షేత్రంలో కొత్త పుంతలు తొక్కేటప్పుడు స్పష్టతకి ఉత్కృష్టమైన స్థానం ఇవ్వాలి. డెకార్ట్ చెప్పినట్లు ‘లోకోత్తరమైన సమస్యలకి పరిష్కారాలు వెతికేటప్పుడు లోకోత్తరమైన స్పష్టత ఉండాలి.’ గేల్వా ఈ మౌలిక సూత్రాన్ని విస్మరించేడు. అందుకనే ఆనాటి గణితజ్ఞులు తమ కఠినమైన హితోపదేశంతో గేల్వాని సన్మార్గంలో పెట్టడానికి ప్రయత్నించి విఫలమయి ఉంటారు. అభిశంసించడానికి బదులు వారు అతనిని అక్కున చేర్చుకుని ఉండుంటే ఈ కుర్రాడు లబ్ది పొంది ఉండేవాడేమో. ఇప్పటికే వంతెన కింద చాల నీరు ప్రవహించింది. గేల్వా ఇక లేడు. జరిగినదానికి ఎవరు బాధ్యులు అని నిష్ప్రయోజనమైన ఆక్షేపణలతో పరస్పరం దూషించుకోవడం కంటె గతాన్ని మరచిపోయి మంచిని చేరదీసి…”

{ఈ కథ వెనుక కథ: నేను అమెరికా వచ్చిన కొత్తలో, 1962లో మా అన్నయ్య స్నేహితుడు సి. రాబర్ట్ వార్నర్ ఈస్ట్ లేన్సింగ్‌లో గణితశాస్త్ర విభాగంలో అసిస్టెంట్ ప్రొఫెసర్‌గా పని చేస్తూ ఉండేవాడు. అన్నయ్య ఇండియా తిరిగి వెళ్ళిపోతూ, మా తమ్ముడి మంచి చెడ్డలు కాస్త చూస్తూ ఉండు, అని చెప్పబట్టి నన్ను ఒకసారి చుట్టపుచూపుగా తన వద్దకు రప్పించుకొని రెండు రోజులు తన ఎపార్టుమెంట్లో ఉంచుకున్నాడు, బాబ్. నేను నా హోమ్ వర్క్ చేసుకుంటూ ఒక పంచఘాత సమీకరణం యొక్క మూలాలు దక్షిణార్థ తలంలో ఉన్నాయో పశ్చిమార్థ తలంలో ఉన్నాయో రౌత్-హర్విచ్ పధ్ధతి ప్రకారం నిర్ణయిస్తూ ఉంటే, “ఆ మూలాల ఉనికి ఏ అర్థ తలంలో ఉన్నాయో నిర్ణయించడం కాదు, వాటి స్థావరాలు నిక్కచ్చిగా ఎక్కడెక్కడ ఉన్నాయో కూడ లెక్క కట్టి చూడరాదూ” అంటూ నన్ను ఇంటి దగ్గర వదిలేసి కాలేజీకి వెళ్ళిపోయాడు. అతను మూడు గంటలలో తిరిగి వచ్చేసరికి నేను ఇంకా కుస్తీ పడుతూనే ఉన్నాను. అప్పుడు బాబ్, “ఇది ఎంతో పేరెన్నిక గన్న సమీకరణం. దీనిని పరిష్కరిస్తూ గేల్వా డ్యూయల్ లో చచ్చిపోయేడు” అని చెప్పేడు. నేను ఇండియాలో ఉన్నప్పుడే గ్రెగరీ పెక్ నటించిన డ్యూయల్ ఇన్ ద సన్ అనే సినిమా చూసి ఉండబట్టి డ్యూయల్ అంటే ద్వంద్వ యుద్ధం అని గ్రహించేను కాని గేల్వా ఎవ్వరో, అతను యుద్ధం ఎందుకు చెయ్యవలసి వచ్చిందో అప్పట్లో తెలుసుకోవాలన్న కుతూహలం కలగలేదు. దరిమిలా గేల్వా పేరు నాకు అప్పుడప్పుడు తారస పడుతూనే ఉండేది. బాబ్ వార్నర్ గుర్తుకి వస్తూనే ఉండేవాడు. ఇప్పుడు నాకు గేల్వా మళ్ళా దర్శనమిచ్చేడు. పాత రోజులు స్మృతిపథంలో మెలిగేయి. కనీసం గేల్వా గురించి రాసి, ఫెర్మా చివరి సిద్ధాంతం పరిష్కారానికి గేల్వా చూపిన దారి ఎలా రహదారి అయిందో చెపుదామని కోరిక కలిగింది. ఈ నేపథ్యంలో ఈ వ్యాస పరంపర రాయడానికి శ్రీకారం చుట్టి ముందుగా గేల్వా మీద ఈ వ్యాసంతో మొదలు పెట్టేను.}

4.10 బీజగణితంలో గుంపు అనే భావం

గేల్వా ప్రతిపాదించిన పరిష్కారానికి మూలస్తంభం గేల్వా ప్రవేశపెట్టిన గుంపు (group) అనే భావం. గణితపరంగా గుంపు అనేది ఒక సమితి (set), ఆ సమితిలో ఉన్న సభ్యులు పాల్గొనగలిగే ఒక ఒక గణిత ప్రక్రియ. ఉదాహరణకి ధన పూర్ణ సంఖ్యలు, ఋణ పూర్ణ సంఖ్యలు, అనగా అనంతవాహినిలా వచ్చే … -3, -2, -1, 0, +1, +2, +3, … అనేవి ఒక సమితి అనుకుందాం. ఈ సమితిలోని సభ్యులతో సంకలనం అనే గణిత ప్రక్రియ చేద్దాం:

4 + 8 = 12

ఇక్కడ, 4, 8 పూర్ణ సంఖ్యలు, వాటిని కలపగా వచ్చిన 12 కూడ పూర్ణ సంఖ్యే. ఈ లక్షణం ప్రదర్శించేయి కనుక, పూర్ణ సంఖ్యలు అనే సమితి సంకలనం చేసేటప్పుడు సంవృతం (closed under addition) అంటారు. ఇటువంటి సందర్భంలో – సంకలన ప్రక్రియతో ఉన్న పూర్ణ సంఖ్యలు ఒక గుంపుగా పరిగణించబడతాయి.

ఇప్పుడు 4, 8 అనే పూర్ణ సంఖ్యలతో విభజన అనే ప్రక్రియ చేస్తే

4/8 = 1/2

అనే భిన్నం వచ్చింది; ఇది పూర్ణ సంఖ్య కాదు. కనుక – పూర్ణ సంఖ్యలు అనే సమితి విభజన చేసేటప్పుడు సంవృతం కాదు. కనుక – విభజన ప్రక్రియతో ఉన్న పూర్ణ సంఖ్యలు ఒక గుంపుగా పరిగణించబడవు.

ఇక్కడ, పూర్ణ సంఖ్యలు అనే సమితిలో అనంతమైనన్ని సభ్యులు ఉన్నాయి. కాని అలా ఉండాలని నియమం ఏదీ లేదు. ‘సాంతమయిన సమితితో మొదలుపెట్టి జాగరూకతతో నిర్మించిన గుంపులు కూడ ఉపయుక్తమైన లక్షణాలు ప్రదర్శించగలవు,’ అన్నాడు గేల్వా. అని, ఒక బహుపద సమీకరణం (polynomial) తీసుకుని, దాని మూలాలు (రెండో, మూడో, నాలుగో, అయిదో, … ఉంటాయి కదా) సాంతమయిన సమితులు అనుకుని వాటితో సాంతమైన గుంపులని నిర్మించి, వాటి ద్వారా ఆ సమీకరణాల మూలాలకి సంబంధించిన విశేషాలు బయటికి లాగొచ్చని నిరూపించేడు.

ఒకటిన్నర శతాబ్దాలు పోయిన తరువాత, గేల్వా వేసిన ఈ పునాది మీద నిలబడి, 1993లో, ఏండ్రూ వైల్స్ 350 సంవత్సరాలబట్టి పరిష్కారం లేకుండా మగ్గుతున్న ఫెర్మా యొక్క చివరి సిద్దాంతాన్ని రుజువు చేసేడు! ఈ రుజువు సాధించడానికి ఆయన ఎలిప్టిక్ కర్వ్ (elliptic curve) మాడ్యులార్ ఫామ్ (modular form) అనే రెండు విలక్షణమైన ద్వంద్వ భావాలని తాళ్ళుగా వాడుకుని, వాటి మధ్య నిచ్చెన మెట్లులా ఒక సంక్లిష్టమైన, 150 పేజీలు పొడుగున్న, ఋజువుని అల్లుకుంటూ వచ్చేడు.

5. ఎలిప్టిక్ వక్రరేఖలు

ఫెర్మా చివరి సిద్ధాంతం పరిష్కరించిన ఘనత ఏండ్రూ వైల్స్‌కి దక్కిందని చెప్పుకున్నాం కదా. ఈ ఏండ్రూ వైల్స్ విద్యార్థిగా ఉన్న దశలో, పరిశోధనాంశాన్ని నిర్ణయించుకునే సందర్భంలో, ఆయన గురువు, ‘నువ్వు ఎలిప్టిక్ వక్రరేఖల మీద పరిశోధన చేస్తే బాగుంటుంది,’ అని సలహా ఇచ్చేరుట. నిజానికి ఎలిప్టిక్ వక్రరేఖలకీ, దీర్ఘవృత్తాలకీ పెద్దగా దగ్గర సంబంధం లేదు; బాదరాయణ సంబంధం ఉంది. ఇప్పుడు ఎలిప్టిక్ వక్రరేఖలు (elliptic curves) అంటే ఏమిటో, వాటికీ గేల్వా ప్రతిపాదించిన ‘గుంపు’ అనే భావానికి, ఫెర్మా చివరి సిద్ధాంతానికీ మధ్య ఉన్న సంబంధ బాంధవ్యాలు ఏమిటో కొంచెం చూచాయగా అర్థం చేసుకుందుకు ప్రయత్నిద్దాం.

5.1 ఎలిప్టిక్ ప్రమేయాలు, ఎలిప్టిక్ వక్రరేఖలు

గుండ్రంగా ఉన్న ఆకారాన్ని వృత్తం అనిన్నీ, కోలగా ఉన్న ఆకారాన్ని దీర్ఘవృత్తం అనిన్నీ అంటాం కదా. ఈ దీర్ఘవృత్తానికే ఇంగ్లీషు పేరు ఎలిప్స్ (ellipse). ఈ దీర్ఘవృత్తపు పరిధి వెంబడి ఒక బిందువు నుండి మరొక బిందువుకి మధ్య ఉన్న దూరాన్ని గణన చెయ్యడానికి వాడే గణిత స్వరూపాన్ని ఎలిప్టిక్ ప్రమేయాలు (elliptic functions) అంటారు. ఎలిప్టిక్ వక్రరేఖలు అన్నా ఎలిప్టిక్ ప్రమేయాలు అన్నా దరిదాపు ఒక్కటే; వక్రరేఖలు అన్న మాట రేఖాగణిత సంప్రదాయం నుండి వస్తే, ప్రమేయాలు అన్న మాట బీజగణిత సంప్రదాయం నుండి వచ్చింది. అందుకనే ఈ శాఖని బీజీయ రేఖాగణితం (algebraic geometry) అంటారు.

చారిత్రకంగా చూస్తే ఎలిప్టిక్ ప్రమేయాల అధ్యయనం ప్రాచీన కాలంలోనే మొదలయింది. ఉదాహరణకి ఈ ప్రహేళికని చూడండి. వరుసక్రమంలో ఉన్న ఏ మూడు పూర్ణాంకాల లబ్దం ఒక వర్గు సంఖ్య అవుతుంది? (Find three consecutive integers whose product is a square.) ఈ సమస్యని బీజ గణిత పరిభాషలో ఇలా చెప్పవచ్చు:

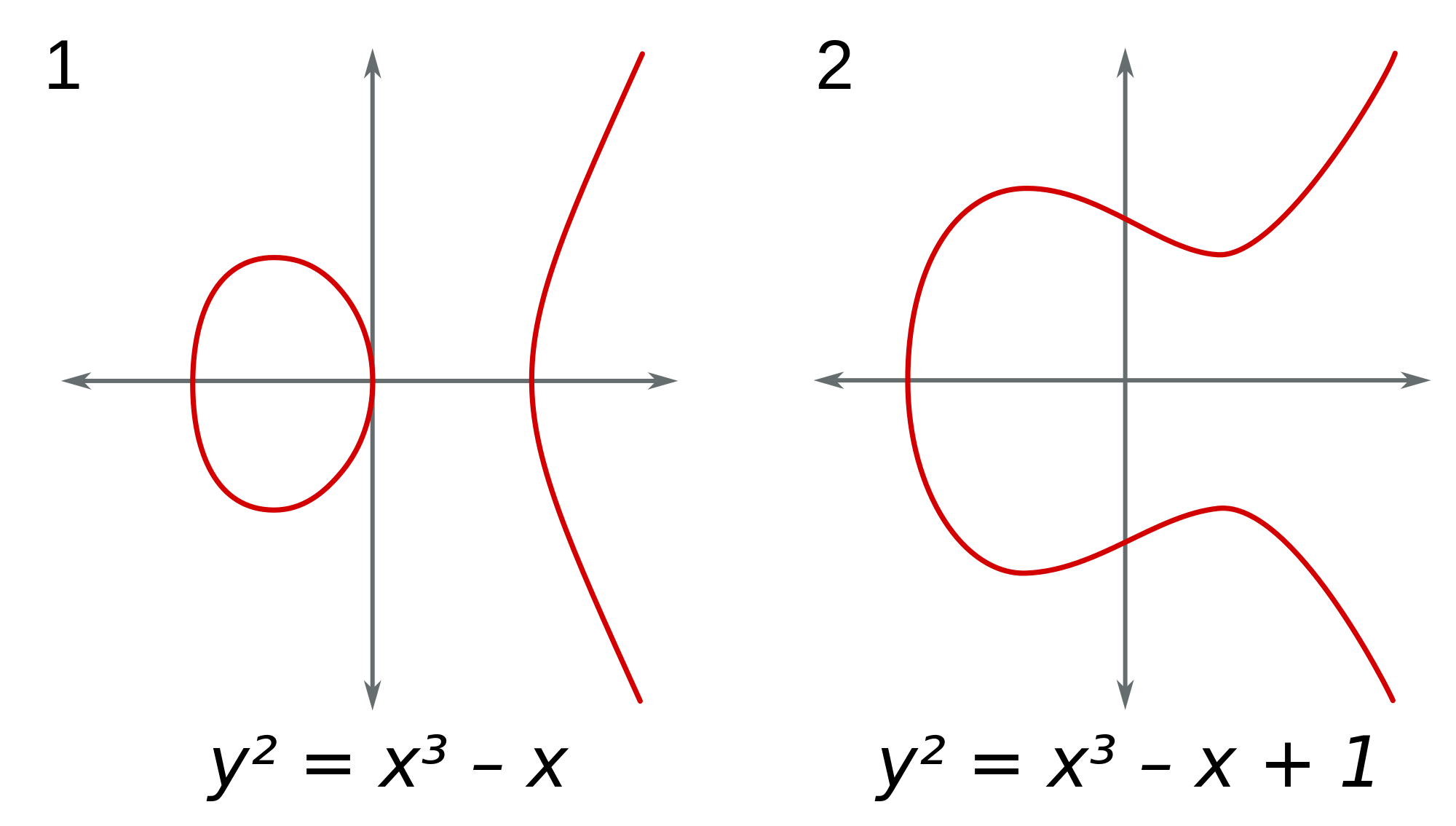
y² = (x −1)x(x + 1) or y² = x³ − x అనే సమీకరణంలో x, y పూర్ణాంకాలు అయినప్పుడు వాటి విలువలు ఏమిటి?

ఈ రకం ప్రహేళికలు సుప్రసిద్ధమైన డయఫాంటైన్ సమీకరణాలకి (Diophantine equations) దారి తీసేయి. డయఫాంటైన్ సమీకరణాలని మూడు జాతులుగా విడగొట్టవచ్చు: తేలికగా లొంగేవి లేదా జాతి 0 లేదా సాధారణ వక్రరేఖలు; కష్టపడితే కాని లొంగనివి లేదా జాతి 1 లేదా ఎలిప్టిక్ వక్రరేఖలు; కష్టపడ్డా లొంగనివి లేదా జాతి 2 లేదా క్లిష్టతమ వక్రరేఖలు.

ఎలిప్టిక్ వక్రరేఖలు

పక్క బొమ్మని చూడగానే కొట్టొచ్చినట్లు కనబడేది వక్రరేఖల సౌష్టత. అడ్డుగా ఉన్న గీతకి (x-అక్షానికి) ఎగువ ఉన్న రేఖ దర్పణ ప్రతిబింబమే దిగువన ఉంది. ఈ సౌష్టతని ఆధారంగా చేసుకునే గేల్వా ఈ సమీకరణాలలో ఒక గుంపు-తత్త్వం ఉందని పసిగట్టేడు. ఆ వివరాలు ఇక్కడ చెప్పదలుచుకోలేదు.

బీజగణితం లోను, కేల్‌క్యులస్ లోను ఎలిప్టిక్ ప్రమేయాలకి చాల ఉపయోగాలు ఉండబట్టి వీటి గురించి అధ్యయనం చిరకాలం నుండీ కొనసాగుతూనే ఉంది. వీటి గురించి మరి కొంచెం తెలుసుకుందాం. ఉదాహరణకి a, b, c పూర్ణాంకాలు అయినప్పుడు

y² = x³ + a x² + b x + c

అనేది ఒక సర్వసాధారణ రూపంలో ఉన్న ఎలిప్టిక్ ప్రమేయం. ఈ ప్రమేయంలో a = 0, b = 0, c = – 2 అయినప్పుడు వచ్చిన

y² = x³ – 2

అనేది ఒక ప్రత్యేక రూపంలో ఉన్న చిన్న ఎలిప్టిక్ ప్రమేయం. ఈ చిన్న ప్రమేయంలో y = 5, x = 3 అనే పూర్ణాంకాలు వాడినప్పుడు ఈ సమీకరణం చెల్లుబాటు అవుతుంది:

5² = 3³ – 2

సరిపోయింది కదా? ఈ చిన్న సమీకరణానికి y = 5, x = 3 అనే ఒక్క పరిష్కారం తప్ప మరొక పరిష్కారం లేదనే నేను అనుకుంటున్నాను. (ఓపిక ఉంటే అవునో కాదో చూడండి.)

ఇప్పుడు సర్వసాధారణ రూపంలో ఉన్న ఎలిప్టిక్ ప్రమేయంలో a, b, c లకి రకరకాల పూర్ణాంకపు విలువలు ఇచ్చుకుంటూ పోతే మనకి అనంతమైనన్ని ఎలిప్టిక్ సమీకరణాలు వస్తాయి. ఇలా వచ్చిన ప్రతి సమీకరణానికీ ఒకటో, అంతకంటె ఎక్కువో – పైన చూపిన విధంగా – పరిష్కారాలు ఉంటాయి. ఫెర్మా కాలానికి ముందునుండీ పరిశోధనలు జరుగుతున్నా వీటి గురించి మనకి ఇంకా పరిపూర్ణమైన అవగాహన రాలేదు.

5.2 ఎలిప్టిక్ సమీకరణాలలోని క్లిష్టత

ఎలిప్టిక్ సమీకరణాలలోని క్లిష్టతని అర్థం చేసుకుందుకి ఈ దిగువ సమీకరణాన్ని చూద్దాం:

x³ – x² = y² + y

దీనికి x = 0, y = 0 ఒక పరిష్కారం అని చెబుతున్నాను. ఇది నిజమే అని ఋజువు చెయ్యడానికి ఈ విలువలు పై సమీకరణంలో ప్రతిక్షేపించి చూద్దాం:

0³ – 0² = 0² + 0 అనగా 0 = 0

సరిపోయింది కదా! ఇంతేనా? ఇంకా పరిష్కారాలు ఉన్నాయా? మరొక పరిష్కారం x = 1, y = 0. ఎందుకంటే

1³ – 1² = 0² + 0 అనగా 0 = 0

సరిపోయింది కదా. ఇంతేనా? ఇంకా పరిష్కారాలు ఉన్నాయా? ఇది హనుమంతుడి తోకలా అలా పెరుగుతూ పోతుందో ఏమో? ఎంతకని చూస్తాం? అనంతమైనన్ని పరిష్కారాలు ఉంటే అప్పుడేమి చేస్తాం?

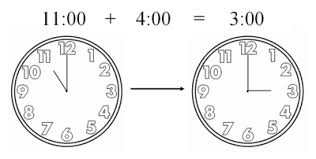
గడియారం (మాడ్యులో-12) గణితం

ఒక పధ్ధతి ఏమిటంటే ఆ హనుమంతుడి తోకని వెనక్కి తిప్పి, ఒక చక్రంలా టాకా వెయ్యడం. వేసి, ఆ చక్రంలో ఇమిడే పరిష్కారాలని మాత్రమే పరిశీలించడం. ఈ రకం గణితాన్ని గడియారం గణితం అని కాని, ఘడీ గణితం (clock arithmetic) అని కాని అంటారు. గణిత పరిభాషలో modulo arithmetic అంటారు. ఇది మనకి పరిచయం ఉన్న పద్ధతే! అనంత వాహినిలా వచ్చే రోజులని లెక్కపెట్టడానికి మనం వార గణితం (week arithmetic) వాడుతున్నాం కదా. ఆది, సోమ, మంగళ, బుధ, గురు, శుక్ర, శని అవగానే మళ్ళా ఆది, సోమ,… అంటూ అందుకుంటాం కదా. గోడ గడియారంలో 1, 2 ,3, …, 12 అయిన తరువాత మళ్ళా 1, 2, 3, … అని అందుకుంటాం కదా. ఉదయం 11 గంటలకి రావలసిన బండి 4 గంటలు లేటు అంటే 11కి 4 కలిపి 15 గంటలు అనమే; ఆ 15 లోంచి 12 తీసేసి సాయంత్రం 3 గంటలు అంటాం. అనగా, ఇక్కడ చేసినది, గణిత పరిభాషలో – మాడ్యులో-12 గణితం. ఈ పద్ధతితో సుఖం ఏమిటంటే మనం వాడవలసిన సంఖ్యలు అనంతంగా పెరిగిపోకుండా కట్టుదిట్టం చేసేం.

గడియారం (మాడ్యులో-5) గుణకారం

గడియారం గణితంలో కూడికలు చేసినట్లే గుణకారాలు కూడ చెయ్యవచ్చు. బొమ్మలో ఒక మాడ్యులో-5 కూడిక పట్టీ, ఒక మాడ్యులో-5 గుణకారం పట్టీ (ఎక్కం) చూపిస్తున్నాను. ఇప్పుడు, మచ్చుకి, మాడ్యులో-5 పద్ధతిలో పైన ఉదహరించిన x³ – x² = y² + y అనే ఎలిప్టిక్ సమీకరణానికి పరిష్కారాలు వెతుకుదాం. (ఈ లెక్క కాగితం, కలం తీసుకుని చెయ్యడం కష్టం కాదు. ప్రయత్నించి చూడండి.)

x = 0, y = 0
x = 0, y = 4
x = 1, y = 0
x = 1, y = 4

అనగా పైన ఉదహరించిన ఎలిప్టిక్ సమీకరణానికి, మాడ్యులో-5 పద్ధతిలో 4 పరిష్కారాలు ఉన్నాయి. లేదా, గణిత పరిభాషలో E₅ = 4 అని రాద్దాం. (E అంటే ఎలిప్టిక్, 5 మాడ్యులో 5ని సూచిస్తుంది, 4 మనకి దొరికిన పరిష్కారాలు.) ఇదే సమస్యని మాడ్యులో-7 పద్ధతిలో చేస్తే 9 పరిష్కారాలు వస్తాయి, లేదా E₇ = 9 అవుతుంది. ప్రయత్నించి చూడండి. ఇదే పద్ధతిలో లెక్క కట్టి ఈ దిగువ చూపిన విలువలు అన్నీ సంపాదించవచ్చు (ఓపిక ఉన్న వాళ్ళు చేసి చూడండి, పెద్ద కష్టం కాదు):

E₁ = 1.
E₂ = 4.
E₃ = 4.
E₄ = 8.
E₅ = 4.
E₆ = 16.
E₇ = 9.
E₈ = 16.
…
…

మామూలు పద్ధతిలో హనుమంతుడి తోకలా పరిష్కారాలు ఎదురవుతున్నాయని మాడ్యులో పద్ధతిని ఆశ్రయించేం. ఇక్కడ గానుగెద్దులా తిరుగుతున్నాం; ఈ తిరుగుడూ అంతు లేకుండానే ఉంది కదా! అయినప్పటికీ, ఈ E-శ్రేణి వల్ల లాభాలు లేకపోలేదు. జంటపెన (double helix) నమూనాలో ఉన్న అరైకామ్లం (DNA) జీవి జాతకాన్ని తనలో ఎలా నిక్షిప్తపరచుకుందో అదే విధంగా ఈ E-శ్రేణి లో ఎలిప్టిక్ సమీకరణాల గుట్టు అంతా నిక్షిప్తం అయి ఉంది. అందుకనే ఏండ్రూ వైల్స్ వీటిని అధ్యయనం చెయ్యడానికి సంకల్పించుకున్నాడు.

ఈ అధ్యాయం ముగించే లోగా ఎలిప్టిక్ వక్రరేఖల పరిష్కారాల లక్షణం ఒకటి మననం చేసుకుందాం. ఎలిప్టిక్ వక్రరేఖలకి అనంతమైనన్ని పరిష్కారాలు ఉన్నప్పటికీ వాటిలో సాంతమైనటువంటి పరిష్కారాలు తీసుకుని వాటితో సంకలన వ్యవకలనాలు చేసి మిగిలిన అనంతమైన పరిష్కారాలని సాధించవచ్చు అని మోర్డెల్ (Louis Mordell) రుజువు చేసేడు. అంటే ఈ సాంతమైన పరిష్కారాలు – గేల్వా చెప్పినట్లు – ఒక గుంపు వలె ప్రవర్తిసున్నాయనే కదా తాత్పర్యం. గేల్వా బహుపద సమీకరణాల సందర్భంలో ప్రవేశపెట్టిన గుంపు అనే భావం ఇక్కడ ఎలిప్టిక్ సందర్భానికి అనువర్తించేమన్నమాట.

6. టనియామా – షిమూరా

మూడవ అధ్యాయం చివరలో ప్రస్థావించిన కుమ్మర్ పరిశోధన ఫలితంగా, ప్రధాన సంఖ్యల దారి వెంబడి వెళితే ఫెర్మా సమస్య పరిష్కారం అయే అవకాశం లేదని తేలిపోవడంతో ఫెర్మా సమస్య వైపు దరిదాపు 150 ఏళ్ళ పాటు ఎవ్వరూ కన్నెత్తి చూసినట్లు లేదు. ఇక్కడా, అక్కడా, చెదురుమదురుగా ప్రయత్నాలు జరిగి ఉండవచ్చు గాక. కాని పెద్దగా కదలిక కనిపించలేదు.

6.1 టనియామా – షిమూరా శిష్టాభిప్రాయం

గొరొ షిమూరా (1930 – )

అది 1954 జనవరి నెల. రెండవ ప్రపంచ యుద్ధంలో జరిగిన పరాభవం నుండి అప్పుడప్పుడే తేరుకుంటోంది జపాను. యుద్ధం తాకిడికి పాఠశాలలు మూతపడిపోవడం వల్ల గొరో షిమూరా (Goro Shimura) చదువు అర్ధంతరంగా ఆగిపోయింది. యుద్ధ విమానాలని తయారు చేసే కర్మాగారంలో పనివాడుగా కుదురుకున్నాడు. కాని చదువు మీద ఆకాంక్ష పోలేదు. పలక, బలపం తప్ప మరొక పరికరం అందుబాటులో లేని గొరో సాయంకాలం ఇంటికి వచ్చిన తరువాత లెక్కలు చేస్తూ కూర్చునేవాడు. యుద్ధం అయిపోయి, శాంతి భద్రతలు నెలకొన్న తరువాత గొరో టోక్యో విశ్వవిద్యాలయంలో చేరేడు. ఏదో లెక్క చేసుకుంటూ ఉండగా ఒక సందేహం వచ్చి ఒక పరిశోధనా పత్రిక సంప్రదించడానికి గ్రంథాలయానికి వెళ్ళేడు. తనకి కావలసిన పత్రిక యుటాకా టనియామా (Yutaka Taniyama) అనే వ్యక్తి పట్టుకెళ్ళేడు. ఆ పుస్తకం తిరిగి రాడానికి రెండు వారాలు పడుతుంది. తను రెండు వారాలు ఆగలేడు, చేస్తూన్న లెక్క మధ్యలో ఆగిపోయింది. అందుకని టనియామాకి, ఒక సారి తనకి కావలసిన వ్యాసం సంప్రదించడానికి వీలవుతుందా? అంటూ ఒక కార్డు ముక్క రాసి పడేసేడు.

వారం తిరక్కుండా టనియామా సమాధానం రాసేడు. ఆశ్చర్యం! తనూ అదే రకం లెక్క చేస్తూ, అదే సందేహం వచ్చి, అదే వ్యాసాన్ని సంప్రదించడానికి ఆ పుస్తకం గ్రంథాలయం నుండి పట్టుకెళ్ళేడుట! ఇద్దరికీ మధ్య స్నేహం కుదిరింది. కలిసి పని చెయ్యడం మొదలు పెట్టేరు.

యుటాకా టనియామా (1927 – 1958)

కలిసి పని చెయ్యడం మొదలు పెట్టడం అంటే మొదలు పెట్టేరు కాని ఈ జంట దున్నపోతు-ఎద్దు జంట లాంటిది. టనియామాకు బద్ధకం. అయినా సరే లేడికి లేచిందే పరుగు అన్నట్లు పని మొదలెట్టేడంటే దూరాలోచనలేకుండా తప్పు దారులు తొక్కే రకం. పడితే లేచి, బట్టలు దులుపుకుని ముందుకి కదిలే రకం. షిమూరా ఇతనికి వ్యతిరేకం. నిష్టాగరిష్టుడు. ఒక పద్ధతిగా ఆలోచించి ఒక అడుగు ముందుకి వేసే రకం. ఆలస్యం అమృతం విషం అన్నది టనియామా మంత్రం అయితే నిదానమే ప్రధానం అనేది షిమూరా మంత్రం. అయినా వీరిద్దరికీ స్నేహం కుదిరింది. టనియామా తొందరపాటుతో తొక్కే తప్పుదారుల వెంబడి వెళితే రత్నాలు దొరుకుతున్నాయి, అనేవాడు షిమూరా. టనియామా పరాకు చిత్తగించే ప్రతిభావంతుడు. జోళ్ళకి ఉన్న తాళ్ళని ముడేసుకోవడానికి ఓపిక లేక అలానే చెప్పులలో కాళ్ళు పెట్టి నడిచేసేవాడుట. ఎప్పుడూ ఒకే రంగు బట్టలు వేసుకునేవాడుట. ఇలాంటివాడు గణిత సమావేశాలలో పులిలా మారిపోయేవాడుట. విద్యార్థులని ఉత్తేజపరచి వాళ్ళ చేత కొత్త పుంతలు తొక్కించేవాడుట.

ఆ రోజులలో జపాను లోని పరిశోధన స్థాయి పాశ్చాత్య దేశాలలో స్థాయికి నాలుగు మెట్లు దిగువనే ఉండేది. అమెరికా లోను, యూరప్ లోనూ పాత చింతకాయ పచ్చడి అని చప్పరించి వదిలేసే సమస్యలనే ఇంకా పట్టుకు వేళ్ళాడుతూ ఉండేవారు. అలాంటి సమస్యలలో ఒకదాని పేరు మాడ్యులార్ ఫామ్స్ (modular forms). టోకియో నగరంలో, 1955లో జరిగిన ఒక అంతర్జాతీయ సమావేశంలో 28 ఏళ్ళ టనియామా మొట్టమొదట తన అభిప్రాయాన్ని ఒక ప్రశ్న రూపంలో వ్యక్తపరచేడు. మూడేళ్ళ తరువాత – టనియామా ఆత్మహత్య చేసుకున్న తరువాత – షిమూరా ఈ అభిప్రాయానికి కండబలం చేకూర్చేడు. ఆ సమావేశానికి హాజరయిన ఏండ్రూ వైల్స్ – అప్పటికే ఎలిప్టిక్ వక్రరేఖల మీద పని చేసున్నాడేమో – ఈ అభిప్రాయంలో పస ఉందని గట్టిగా నమ్మి దాని మీద పరిశోధన మొదలుపెట్టేడు.

6.2 గుళిక స్వరూపాలు

గణిత రంగంలో, మాడ్యులార్ ఫామ్స్ లేదా గుళిక స్వరూపాలు అనేవి విలక్షణమైన శాల్తీలలో విలక్షణమైనవి. ఒక విధంగా చూస్తే వాటిలో సౌష్ఠవం ఉంది, సౌందర్యం ఉంది. మనందరికీ సుపరిచితమైన సంకలనం, వ్యవకలనం, గుణకారం, భాగారాలతో పాటు మాడ్యులార్ ఫామ్ అనేది అయిదో గణిత ప్రక్రియ అని కొందరు దీనిని అభివర్ణించేరు. టనియామా, షిమూరా అధ్యయనం చేసిన గుళిక స్వరూపాలలో ఎంత సౌష్ఠవం ఉందంటే ఆ స్వరూపాలని అనంతమైనన్ని విధాలుగా పక్కకి జరిపినా, గుండ్రంగా తిప్పినా, అద్దంలో ప్రతిబింబించినా వాటి స్వరూపం మారినట్లు కనబడదు. బల్ల మీద పరచిన గళ్ళ దుప్పటిని ఇటూ అటూ జరిపినా, గుండ్రంగా తిప్పినా కంటికి మార్పు కనిపించదు కదా! అలాగన్నమాట!

ఎషర్ సర్కిల్ లిమిట్ 4.

టనియామా, షిమూరా పని చేసినది చదునైన బల్ల మీద కాదు; చతుర్మితీయ అతివలయ ఆవరణంలో (four-dimensional hyperbolic space.) త్రిమితీయ యూక్లిడ్ ఆవరణానికి అలవాటు పడ్డ మనకి చతుర్మితీయ అతివలయ ఆవరణం అవగాహనలోకి రాదు. ఎషర్ (M.C. Escher) ఈ రకం ఆవరణ ఎలా ఉంటుందో బల్లపరుపుగా ఉన్న ప్రదేశం మీద చిత్రించి చూపించేడు. ఎషర్ పేరు వినకపోయినా ఆయన వేసిన చిత్రాలు మీరు చూసే ఉంటారు. చతుర్మితీయ అతివలయ ఆవరణంలో గుళిక స్వరూపాలని అనేక ఆకారాలలో, అనేక ప్రమాణాలలో నిర్మించవచ్చు. ఒక గుళిక స్వరూపానికి, మరొక గుళిక స్వరూపానికీ మధ్య ఉండే తేడా ఈ ఆకారాలు, ప్రమాణాలు ఏయే పాళ్ళ్ళల్లో పడ్డాయో దాన్ని బట్టి ఉంటుంది. ఒక ఆవకాయ ఉపమానం చెబుతాను. కాయావకాయ, బెల్లపావకాయ, ఉల్లావకాయ, మాగాయ, తొక్కుడు పచ్చడి, వగైరాలన్నిటిలోనూ మామిడికాయలు, కారం, ఉప్పు, ఆవ పిండి, నూనె, వగైరా ఘటక ద్రవ్యాలు ఉంటాయి కాని ప్రతి దాంట్లోనూ వాటి ఆకారాలు (కాయలు, చెక్కలు, పెద్ద ముక్కలు, చిన్న ముక్కలు, చెక్కిన కోరు, వగైరా) మారతాయి, వాటి పాళ్ళు మారతాయి. అలాగే అనుకొండి. ఉదాహరణకి మన గుళిక స్వరూపాలలో పడే ఘటక ద్రవ్యాలని M₁ = కాయలు, M₂ = కారం, M₃ = ఉప్పు, M₄ = ఆవ, M = ఉల్లి … అనుకుంటూ వెళదాం. ఇప్పుడు ఒక గుళిక స్వరూపంలో (ఒక రకం ఆవకాయ) మామిడికాయలు ఒక పాలు (M₁ = 1), కారం మూడు పాళ్ళు (M₂ = 3), ఉప్పు రెండు పాళ్ళు (M₃ = 2), … అనుకుంటూ వెళ్ళవచ్చు. ఇప్పుడు ఈ రకం ఆవకాయని పెట్టడానికి సూత్రం M₁ = 1, M₂ = 3, M₃ = 2, … అవుతుంది కదా. ఘటక ద్రవ్యాల పాళ్ళు మార్చితే ఆవకాయ స్వరూప, స్వభావాలు మారిపోయినట్లే ఇక్కడ M₁, M₂, M₃, …, అనే శ్రేణిలో విలువలు మారితే గుళిక స్వరూపం మారిపోతుంది! మారిపోయిన స్వరూపానికి సౌష్ఠత ఉండి మరొక గుళిక స్వరూపం పొందవచ్చు లేదా ఉన్న సౌష్ఠత ఊడి గుళిక స్వరూపం నాశనం కావచ్చు.

గత అధ్యాయంలో చదివిన ఎలిప్టిక్ ప్రమేయాలకి E-శ్రేణి ఎలా ఆయువు పట్టయిందో, అదే విధంగా గుళిక స్వరూపాలకి ఈ M-శ్రేణి ఆయువు పట్టు. ఎలిప్టిక్ ప్రమేయాలు గ్రీకుల కాలం నుండీ ఉన్నాయి. వీటికి సౌష్ఠవం లేదు. గుళిక స్వరూపాలు ఇటీవలి కాలంలో ఆవిష్కరించబడ్డాయి. వీటి మనుగడకి సౌష్ఠత ముఖ్యం. ఒకరి ప్రపంచం E-ప్రపంచం అయితే మరొకరిది M-ప్రపంచం. ఎవరి ప్రపంచం వారిది. వీటి మధ్య కనీసం బాదరాయణ సంబంధం ఉండొచ్చేమో అని శంకించినవాళ్ళు కూడ ఎవ్వరూ లేరు. గణిత మహాసముద్రంలో ఇదొక ద్వీపం, అదొక ద్వీపం. అటువంటిది, ఊరు పేరు లేని టనియామా, షిమూరాలు అకస్మాత్తుగా ఊడిపడి ఎలిప్టిక్ ప్రమేయాలు, గుళిక స్వరూపాలు పైపైకి అలా కనిపిస్తూన్నా, రెండూ ఒక్కటే అన్నారు. అని, గణిత ప్రపంచంలో ఒక భూకంపం సృష్టించేరు. భౌతిక శాస్త్రంలో అయస్కాంత తత్త్వం, విద్యుత్ తత్త్వం పైపైకి తేడాగా కనిపిస్తూన్నా నిజానికి ఒకటే అని మేక్స్‌వెల్ (James Maxwell) అనలేదూ, అలాగని అనుకొండి.

టనియామా, షిమూరా – ఎలిప్టిక్ ప్రమేయాలు, గుళిక స్వరూపాలు పైపైకి తేడాగా కనిపిస్తూన్నా, రెండూ నిజానికి ఒక్కటే, అని అంటూ కొన్ని ఉదాహరణలు చూపించేరు. ఎలా? ఒక ఎలిప్టిక్ ప్రమేయం తీసుకుని దాని E-శ్రేణి విలువలని లెక్క కట్టేరు. అచ్చం అదే విలువలతో ఉన్న ఒక గుళిక స్వరూపం యొక్క M-శ్రేణిని ఉదాహరణగా చూపించేరు. ఇలా ఒక ఉదాహరణ చూపిస్తే సరిపోతుందా? అది కేవలం కాకతాళీయం కావచ్చు. మరొక ఉదాహరణ చూపించేరు. అదీ కాకతాళీయం కావచ్చు కదా అన్నారు. ఇలా ఎన్ని ఉదాహరణలు చూపించగలరు? పూర్వం పైథాగరోస్ సిద్ధాంతం రుజువు చెయ్యవలసిన సందర్భంలో ఎదురైన పరిస్థితే మళ్ళా ఎదురైంది. రుజువు లేకుండా ఉండిపోయిన ఈ గమనికకి టనియామా – షిమురా శిష్టాభిప్రాయం అని పేరు పెట్టి వదిలేసేరు. (L-functions of elliptic curves over any number field exhibit automorphic properties. A partial and refined case of this conjecture for elliptic curves over rationals is called the Taniyama–Shimura conjecture or the modularity theorem.)

రెండు విభిన్నమైన శాఖల మధ్య ఒక వంతెన ఉండడం వల్ల ఉపయోగాలు ఉంటాయి. ఉదాహరణకి గుణకారాలు చెయ్యడం కష్టం, కూడికలు చెయ్యడం తేలిక. కనుక గుణకారాలు చెయ్యడానికి బదులు వాటి లాగరిథమ్‌లు తీసుకుని ఆ లాగరిథమ్ లని కూడి, ఆ మొత్తానికి ఏంటీ లాగరిథమ్ తీసుకోవడం మనం ఉన్నత పాఠశాలలోనే నేర్చుకున్నాం. ఇలాంటి ఉదాహరణలు కొల్లలుగా కనిపిస్తాయి. (ఉత్సాహం ఉన్న వారికి మాత్రమే: time-to-frequency domain.) ఇదే విధంగా ఎలిప్టిక్ రంగంలో ఇబ్బంది పెట్టే సమస్యలకి గుళిక రంగంలో పరిష్కారం వెదకడం సాధ్యపడింది. ఇది ఎంతవరకు వచ్చిందంటే, టనియామా – షిమూరా శిష్టాభిప్రాయం నిజమైతే ఫెర్మా సమస్యని పరిష్కరించడం జరిగిపోయినట్లే! అని అంతా అనుకునే వరకూ వచ్చింది.

ఇటువంటి మేధస్సు ప్రదర్శించిన టనియామా నవంబరు 17, 1958 నాడు ఆత్మహత్య చేసుకుని చచ్చిపోయేడు. టనియామా ప్రేమలో పడ్డాడనిన్నీ, మిసాకో సుజూకి అనే అమ్మాయిని పెళ్ళి చేసుకుందికి ఒప్పుకున్నాడనిన్నీ, కొత్త కాపురానికని ఒక ఇంటిని కూడ అద్దెకి తీసుకున్నాడనిన్నీ వార్తలు వచ్చేయి. టనియామా ఆత్మహత్య చేసుకోవలసిన అవసరం ఎందుకు వచ్చిందో అర్థం కాక అతని స్నేహితుడు షిమూరా చాల మనోవ్యధకి గురి అయాడు. జత కుదరని మిసాకో సుజూకిని ఎలా ప్రేమించేడో అర్థం కావడం లేదంటూ షిమూరా కుమిలిపోయేడు. ఆత్మహత్య చేసుకోబోయే ముందు రాసిన లేఖలో – ఆత్మహత్య చేసుకుని చచ్చిపోవాలన్న కోరిక లేదు. ఇటీవల శారీరకంగానూ, మానసికంగానూ బాగా అలసిపోయి ఉన్నాను. నేను ఎందుకు చచ్చిపోతున్నానో నాకే తెలియదు. ఇది ఎవ్వరి తప్పిదమూ కాదు. ఎందుకో భవిష్యత్తు అంతా చీకటిగా కనిపిస్తోంది. నా మరణం వల్ల ఒక వ్యక్తి ఎక్కువ బాధ పడవచ్చు. ఈ సంఘటన వల్ల ఆ వ్యక్తి భవిష్యత్తు మీద అపోహలు పడకుండా ఉంటే చాలు’నని రాసి చచ్చిపోయేడు.

ఈ ఆత్మహత్య జరిగిన కొద్ది వారాలలో మరొక విషాదమైన సంఘటన జరిగింది. మిసాకో సుజూకి కూడ ఆత్మహత్య చేసుకుంది. ఆమె వదలి పెట్టిన అంతిమ లేఖలో, ‘మేము ఎక్కడికి వెళ్ళినా ఒకరిని మరొకరు వదలి ఉండమని ప్రమాణం చేసుకున్నాము. అతను ఇక్కడ నుండి వెళ్ళిపోయాడు కనుక నేనూ అతని వెంట వెళ్ళాలి,’ అని రాసుకుంది.

6.2 టనియామా – షిమూరా శిష్టాభిప్రాయానికీ ఫెర్మా సమస్యకీ మధ్య లంకె

టనియామా – షిమూరా శిష్టాభిప్రాయనికి ఫెర్మా సమస్యకీ మధ్య లంకె ఏమిటో అర్థం అవాలంటే 1984 లో జెర్మనీలో జరిగిన ఒక గణిత సమావేశానికి వెళ్ళాలి. వెళదాం, రండి. ఈ సమావేశంలో గెర్హార్డ్ ఫ్రే (Gerhard Frey) అనే వ్యక్తి లేచి, ప్రసంగం మొదలు పెట్టి, నల్ల బల్ల దగ్గర నిలబడి ఫెర్మా చివరి సమస్య లోని సమీకరణాన్ని రాయడం మొదలు పెట్టేడు:

xⁿ + yⁿ = zⁿ, n > 2

ఫెర్మా ఏమన్నాడు? ఈ సమస్యకి పూర్ణాంక పరిష్కారం లేదు – అన్నాడు. గెర్హార్డ్ ఫ్రే ఏమన్నాడు? ఒకవేళ కనీసం ఒక్క పరిష్కారం ఉంటేనో? – అని అడిగేడు. ఇలాంటి పిదపకాలపు పరిష్కారం ఉంటేగింటే దానిని x = A, y = B, z = C అని అనుకోమన్నాడు. అలా అనుకున్నప్పుడు, పై సమీకరణం ఈ దిగువ చూపిన విధంగా కనిపిస్తుంది:

Aⁿ + Bⁿ = Cⁿ, n > 2

ఇప్పుడు శాస్త్రోక్తమైన కొన్ని గణిత గారడీలు చేసి, పై సమీకరణాన్ని గెర్హార్డ్ ఫ్రే ఈ దిగువ చూపిన విధంగా అమర్చేడు (వివరాలు మనకి అనవసరం).

y² = x³ + (A^N – B^N) x² – A^N B^N

ఇది చూడడానికి ఎలిప్టిక్ సమీకరణంలా ఉంది కదా. అంటే ఏమిటన్నమాట? ఫెర్మా సమస్యకి పరిష్కారం అంటూ ఉండుంటే ఆ సమస్యని ఎలిప్టిక్ సమీకరణంలా మార్చి రాయవచ్చు. ఈ సమీకరణం సూచించే వక్రరేఖ లక్షణాలు పరిశీలించి చూస్తే అవి టనియామా-షిమూరా శిష్టాభిప్రాయానికి బద్ధమై ఉండకుండా వ్యతిరేకంగా ఉన్నాయి. కనుక గెర్హార్డ్ ఫ్రే నిర్మించిన సమీకరణం ఎలిప్టిక్ కాదా? అంటే గెర్హార్డ్ ఫ్రే ఊహించిన A, B, Cలు ఫెర్మా సమస్యకి పరిష్కారం కాదన్నమాట! ఒక కోయిల కూసినంత మాత్రాన వసంతం వచ్చేసినట్లేనా? ఇల్లలకగానే పండగ చేసేసుకోవడమేనా? ఇక్కడ ఒక్క సందర్భంలో గమనించిన లక్షణాన్ని సిద్ధాంతపు స్థాయికి లేవనెత్తాలి. గెర్హార్డ్ ఫ్రే ఆ పని చెయ్యలేక పోయాడు. చివరికి 1986లో కెన్ రిబెట్ (Kenneth Ribet) కావలసిన రుజువుని చూపించేడు. అది ప్రచురణ పొందడానికి నాలుగేళ్ళు పట్టింది.

ఇదే విషయాన్ని మరొక కోణం నుండి చెబుతాను. గెర్హార్డ్ ఫ్రే తయారు చేసిన ఎలిప్టిక్ సమీకరణం చాల విలక్షణమైనది అయి కూర్చుంది. ఎలా అంటారా? ఈ ఎలిప్టిక్ సమీకరణానికి సంబంధించిన E-శ్రేణి చాల విలక్షణంగా ఉందిట. ఎంత విలక్షణంగా ఉందంటే దానితో జత కూర్చవలసిన M-శ్రేణిని పుట్టించే గుళిక స్వరూపం ఉందని ఋజువు చెయ్యడం దరిదాపు అసంభవం అట! అంటే ఏమిటన్నమాట? టనియామా-షిమూరా శిష్టాభిప్రాయం నిజమైన పక్షంలో పైన చూపిన ఎలిప్టిక్ సమీకరణం అస్తిత్వానికి సావకాశం లేదు. అనగా మనం అనుకున్నట్లు A, B, Cలు ఫెర్మా సమీకరణానికి పరిష్కారం ఇవ్వవు. (ఈ రకం తర్కం గణితంలో సర్వసాధారణం.) దీని నీతి ఏమిటన్నమాట? టనియామా-షిమూరా శిష్టాభిప్రాయం నిజమే అని రుజువు చేస్తే ఫెర్మా సమస్య పరిష్కారం పొందినట్లే! అదీ తర్కం.

ఒక మనవి: పైన ఉపయోగించిన తర్కం అర్థం అవడం కష్టం. ఈ రకం రుజువుని ఖండన ఉపపత్తి (proof by contradiction) అంటారు. అనగా ఒక సిద్ధాంతాన్ని రుజువు చెయ్యడానికి ఒక పరిష్కారాన్ని ప్రతిపాదిస్తాం. అలా ప్రతిపాదించిన పరిష్కారం హేతువిరుద్ధంగా ఉందని రుజువు చేస్తాం. ఇక్కడ మనం చేసినది అదే. టనియామా-షిమూరా శిష్టాభిప్రాయం నిజమే (అనగా, ప్రతి ఎలిప్టిక్ ప్రమేయమూ గుళిక స్వరూపాన్ని ప్రదర్శిస్తుంది) అని నిరూపించగలిగితే దాని పర్యవసానంగా ఫెర్మా శిష్టాభిప్రాయం కూడ నిజమే అవుతుందని రిబెట్ రుజువు చేసేడు. మూడు వందల ఏళ్ళబట్టి మూలని పడి మగ్గుతూన్న సమస్యకి పరిష్కారం దొరుకుతుందనే ఆశ మొదలయింది.

ఇహ పిల్లి మెళ్ళో ఎవ్వరో ఒకరు గంట కట్టాలి!

7. విజయ కేతనం ఎగరేసిన ఏండ్రూ వైల్స్

7.1 ఇప్పటి దాకా జరిగిన కథ

ఫెర్మా ఈ సిద్ధాంతాన్ని 1637లో ఉటంకించేరని మనం నమ్మవచ్చు. ఆయన – ఒకదానితో మరొకటి సమం కాని ఏ మూడు ధన పూర్ణ సంఖ్యలు a, b, c వాడినా కూడ ఈ దిగువ చూపిన సమీకరణం చెల్లనేరదు, అన్నాడు.

aⁿ + bⁿ = cⁿ, n > 2

ఈ సమీకరణం, ఒక ప్రత్యేక సందర్భంలో, అనగా n = 2 అయినప్పుడు a² + b² = c² అవుతుంది. అప్పుడు ఈ సమీకరణంలో a, b, c లు ధన పూర్ణ సంఖ్యలు అయినప్పుడు ఇది పైథాగొరోస్ సిద్ధాంతం అని మనందరికీ తెలుసు. కాని n > 2 – అనగా, n అనే బీజం 2 కంటె పెద్దది అయినప్పుడు ఈ సమీకరణం చెల్లదు అన్నాడు ఫెర్మా.

ఫెర్మా వెలిబుచ్చిన అభిప్రాయం కొన్ని ప్రత్యేక సందర్భాలలో (అనగా, n = 3, n = 4, n = 5, n = 7) ఒప్పే అని ఫెర్మా, ఆయిలర్, ప్రభృతులు రుజువు చేసేరు. తరువాత n = కొన్ని ప్రత్యేకమైన ప్రధాన సంఖ్యలు అయిన సందర్భాలలో కూడ ఫెర్మా అభిప్రాయం ఒప్పే అని సోఫీ జెర్మైన్ చూపించింది. కాని ఫెర్మా వెలిబుచ్చిన శిష్టాభిప్రాయం n > 2 అయిన అన్ని సందర్భాలలోనూ (అనగా, n పూర్ణ సంఖ్య అయిన అన్ని సందర్భాలలోనూ) ఒప్పే అని ఎవ్వరూ రుజువు చెయ్యలేకపోయేరు. చివరికి 358 సంవత్సరాల తరువాత, 1995లో ఏండ్రూ వైల్స్ – రిచర్డ్ టేలర్ (Richard Taylor) సహాయంతో – ఫెర్మా అభిప్రాయం ఒప్పే అని రుజువు చేసి చూపించేడు. రుజువు ప్రచురించడం అయిన తరువాత, కొన్ని ఏళ్ళ తర్జనభర్జనలు అయిన తరువాత, ఆ రుజువులో లొసుగులు కనబడలేదని అంతా ఒప్పుకున్నారు.

ఈ రుజువు చెయ్యడానికి ఎంతో గణనీయమైన స్థాయిలో ఉన్న గణితం వాడవలసి వచ్చింది. ఈ రకం గణితం ఫెర్మా కాలంలో లేదు; తనకి తెలిసిన రుజువు పుస్తకం ఉపాంతంలో పట్టదు అంటూ ఫెర్మా ఎందుకు వ్యాఖ్యానించేరో మనకి తెలియదు. మూడొంతులు ఆయన అనుకున్న రుజువు నిజంగా రుజువు కాదన్నమాట.

ఫెర్మా వెలిబుచ్చిన అభిప్రాయం రుజువు చెయ్యడానికి శతాబ్దాలపాటు జరిగిన ప్రయత్నాలు అన్నీ వమ్ము కాగా, 1950-1960 ప్రాంతాలలో జపానులో యుటాకా టనియామా చేసిన సూచనల ప్రకారం గొరో షిమూరా తయారు చేసిన గుళిక సిద్ధాంతం (Modularity Theorem) మూల స్తంభం అయింది. ఈ గుళిక సిద్ధాంతం ఏమి చేసిందంటే ఎలిప్టిక్ వక్రరేఖలకి, గుళిక స్వరూపాలకి (modular forms) మధ్య అవినాభావ బంధం ఉందని ఉద్ఘాటించింది. ప్రత్యేకించి ప్రతి నిష్ప ఎలిప్టిక్ వక్రరేఖకి జతగా ఒక గుళిక స్వరూపం ఉంటుందని చెప్పింది. కాని రుజువు చెయ్యలేదు కనుక అది శిష్టాభిప్రాయంగానే మిగిలిపోయింది; సిద్ధాంతం స్థాయికి ఎదగలేదు. అది సిద్ధాంతం స్థాయికి ఎదిగితే ఫెర్మా సమస్య పరిష్కారం అయినట్లే అని అంతా ఒప్పుకున్నారు.

ఆండ్రూ వైల్స్ (1953 – )

చివరికి టనియామా-షిమూరా శిష్టాభిప్రాయాన్ని గుళిక సిద్ధాంతం స్థాయికి లేవనెత్తుతూ ఏండ్రూ వైల్స్ 23 జూన్, బుధవారం, 1993న కేంబ్రిడ్జ్ విశ్వవిద్యాలయంలో జరిగిన సభలో, ‘ఎలిప్టిక్ వక్రరేఖలు, గేల్వా ప్రాతినిధ్యాలు’ అనే అంశం మీద మూడు రోజులు ప్రసంగించేరు. సెప్టెంబరు 1993లో ఈ రుజువులో చిన్న లొసుగు కనబడింది. ఆ లొసుగుని రిచర్డ్ టేలర్ సహాయంతో సరి చేసి, తిరిగి మే 1995లో ప్రచురించేరు. దరిదాపు 150 పేజీలు పొడుగున్న ఈ రుజువుని సాధించడానికి ఏండ్రూ వైల్స్‌కి ఏడేళ్ళు పట్టింది.

ఏండ్రూ వైల్స్ సాధించిన రుజువులో మొదట అంచెగా ఎలిప్టిక్ వక్రరేఖలని గేల్వా గుంపుల కోణంలో నరుక్కు రావడం. రెండవ అంచెగా సమస్యని, డిరిక్లే క్లాస్ నంబర్ ఫార్ములా (Dirichlet’s class number formula) వలె రాయడం. మూడవ అంచెగా ఆ ఫార్ములాని రుజువు చెయ్యడం.

7.2 రుజువు యొక్క నఖ చిత్రం

ఏండ్రూ వైల్స్ సాధించిన రుజువుని ఇప్పుడు సమగ్రంగా మరొక కోణం నుండి కూడ అర్థం చేసుకుందాం:

మొదటగా ఫ్రే ఊహ సరి అయిన మార్గంలోనే ఉందని రుజువు. అనగా, గత అధ్యాయంలో చెప్పుకున్న ఫ్రే ప్రతిపాదించిన ఎలిప్టిక్ వక్రరేఖకి (ఇప్పుడు దానిని ఫ్రే వక్ర రేఖ అని పిలుస్తున్నారు) అస్తిత్వం అంటూ ఉంటే దానికి గుళిక తత్త్వం ఉండదు. (First, it is necessary to show that Frey’s intuition was correct: that the above elliptic curve (now known as a Frey curve), if it exists, is always non-modular.) ఫ్రే ఈ సంగతిని కడతేరా రుజువు చెయ్యలేదు. అక్కడ మిగిలిపోయిన ముక్కని ఎప్సిలాన్ శిష్టాభిప్రాయం (Epsilon conjecture) అనేవారు. ఈ శిష్టాభిప్రాయాన్ని రిబెట్ రుజువు చేసేడు కాబట్టి ఇప్పుడు దీనిని రిబెట్ సిద్ధాంతం (Ribet Theorem) అంటున్నారు.

రెండవ అంచెగా గుళిక సిద్ధాంతాన్ని (Modularity Theorem) రుజువు చెయ్యడం. అనగా టనియామా-షిమూరా శిష్టాభిప్రాయాన్ని సిద్ధాంతపు స్థాయికి లేవనెత్తి రుజువు చెయ్యడం. అనగా, అన్ని ఎలిప్టిక్ వక్రరేఖల యెడల కాకపోయిన, కనీసం సెమీ స్టేబుల్ ఎలిప్టిక్ వక్రరేఖల యెడల నిజం అని రుజువు చెయ్యడం.

7.3 ఈ మహాయాగంలో ఎవరి ఘనత ఎంత?

‘సఫలమైన మహా ప్రయత్నానికి అందరూ తండ్రులే! విఫలమైన ప్రయత్నాలు మాత్రం అనాథలు’ అనే అర్థం స్ఫురించే సామెత ఒకటి ఇంగ్లీషులో ఉంది. ఫెర్మా సిద్దాంతం రుజువు చెయ్యడం పూర్తి అయింది కనుక ఈ ఫలితం సాధించిన ఘనత ఎవ్వరిది, ఏ దేశం వారిది అన్న ప్రశ్నలు ఉదయించక మానవు. ఈ క్రతువు ఒక్కరి చేతుల మీదుగా పూర్తి కాలేదన్నది స్పష్టం అవుతూనే ఉంది.

సమస్య ప్రతిపాదించిన ఘనత, మొదట్లో ఏయే మార్గాలు సుగమం కాదో ప్రయాణించి నిర్ధారించిన ఘనత చాలా మట్టుకి ఫ్రాన్స్ దేశానికి చెందుతుంది. చివరికి సాధించిన రుజువు కూడా, చంద్రశాఖా న్యాయంలా, ఫ్రాన్స్ దేశపు గేల్వా చూపించిన దారిలోనే దొరికిందని మనం మరువ కూడదు. తరువాత జపాను దేశపు టనియామా, షిమూరాల జంట ఈ సిద్ధాంతాన్ని దరిదాపుగా రుజువు చేసేసేరు. వారు వడ్డించిన విస్తరికి వైల్స్ వచ్చి అభిఘారం చేసేరు. ఆ అభిఘారం కూడా ఎడం చేత్తో చేసేరనిపిస్తుంది. ఈ సమస్య సాధించిన ఘనత (అనగా టనియామా-షిమూరా శిష్టాభిప్రాయం నిజమే అని రుజువు చేసిన ఘనత) తనకి దక్కదేమోనన్న భయంతో వైల్స్ ఏడేళ్ళ పాటు తను చేస్తూన్న పని ఎవ్వరికీ తెలియకుండా రహస్యంగా దాచేడు. తన రుజువుని బట్టబయలు చేసి ప్రచురించ దలుచుకున్న తరుణంలో, ఆ రుజువుని పరిశీలకులు నిశితంగా పరీక్షించి నిగ్గు తేలుస్తూన్న సమయంలో, ఆ అందులో ఒక లొసుగు కనిపించింది. మొదట్లో చిన్న లొసుగు అనుకున్నది కాస్తా పెరిగి పెద్దదై ఈ బృహత్ ప్రయత్నానికి తిలోదకాలు ఇచ్చేదామనుకున్న తరుణంలో మరొక్క చివరి చూపు చూస్తూ ఉండగా ఆ లొసుగుకి పరిష్కార మార్గం ఆయనకి తట్టింది. ఈ మార్గం వెంట రుజువు పూర్తి చెయ్యటానికి ఆయనకి రిచర్డ్ టేలర్ (Richard Taylor) సహాయం చేసేడు.

ఫెర్మా సిద్ధాంతం రుజువు చెయ్యడానికి కీలకమైన పాత్ర వహించినవారిలో ముఖ్యులు: గేల్వా, టనియామా-షిమూరా, రిబెట్, టేలర్. వీరు వేసిన మెట్ల మీదుగా పైకి ఎక్కి విజయకేతనం ఎగరేసిన వ్యక్తి ఏండ్రూ వైల్స్. టనియామా-షిమూరా ప్రతిపాదించిన గుళిక సిద్ధాంతం (Modular Theorem) వైల్స్ విజయానికి ఆయువుపట్టు. ఈ మహత్కార్యాన్ని సాధించిన ఘనత ఎవరెవరికి ఎంతెంత అని వాటాలు వెయ్యవల్సి వస్తే – నా అభిప్రాయంలో వైల్స్ వాటా 40%, టనియామా-షిమూరాలకి ఉమ్మడిగా 30%, దారి చూపిన గేల్వాకి 10%, రిబెట్, టేలర్లకి ఉమ్మడిగా 10%, మిగిలిన వారికి 10%. వీరందరూ తలొక చెయ్యి వేస్తే కాని పని జరగలేదు కదా!

7.4 మరొక సారి రామానుజన్

రామానుజన్ మరి కొన్నాళ్ళు బతికి ఉంటే ఈ సమస్యని ఆయన పరిష్కరించి ఉండేవారని ఊహాగానం చెయ్యడం కేవలం గాలిలో మేడలు కట్టడం కాదు. వైల్స్ రూపొందించిన పరిష్కారానికి మూలస్తభం అనదగ్గ ఎలిప్టిక్ వక్రరేఖలనే తీసుకుందాం. వీటి జాతికే చెందినవి, వీటి కంటె క్లిష్టమైనవి అయిన K3 surface అనే భావనతో రామానుజన్ కొద్దిగా చెలగాటాలు ఆడేరని, ఎలిప్టిక్ వక్రరేఖ అనే భావాన్ని సాధారణీకరిస్తే ఈ K-3 surface వస్తుందనీ వినికిడి. సైన్ (sine), కోసైన్ (cosine) వంటి ప్రమేయాలని సాధారణీకరిస్తే మాక్ తీటా ప్రమేయాలు (mock theta functions) వచ్చినట్లే ఇక్కడ కూడ ఏదో మెలిక ఉంది. ఆయన నోటు పుస్తకాలలో ఉన్న సమీకరణాలని అర్థం చేసుకోగలిగే స్థోమత మనకి ఉంటే ఫెర్మా చివరి సిద్ధాంతానికి అందమైనదీ, తేలికైనదీ అయిన మరొక రుజువు దొరకొచ్చు. దొరుకుతుందని నా ఆశ, దొరకాలని నా అభిలాష!

7.5 చివరి సిద్ధాంతం మీద చివరి జోకు!

అమెరికాలోనే కాదు ఇంగ్లీషు అర్థం అయే దేశాలన్నిటిలోను బహుజనాదరణ పొంది, వారం వారం రివాజుగా వచ్చే ఒక టెలివిజన్ సినిమా కార్యక్రమం పేరు ద సింప్సన్స్ (The Simpsons.) ఇందులోని పాత్రలన్నీ కొంటెవే! ఈ చిత్రం కథానాయకుడి పేరు హోమర్. ఈ కథాస్రవంతిలో, Homer అనే మకుటంతో ఉన్న ఉదంతంలో, నేపథ్యంలో ఉన్న ఒక నల్లబల్ల మీద 1782¹² + 1841¹² = 1922¹² అనే సమీకరణం కనబడుతుంది! ఫెర్మా సమస్యతో పరిచయం ఉన్న ప్రేక్షకలోకం ఠకీమని లేచి కూర్చుంది. అంతా కళ్ళు నులుపుకున్నారు. ఔరా! అనుకున్నారు. గబగబా కంప్యూటర్ల దగ్గరకి పరుగెట్టేరు. లెక్క కట్టి చూసుకుంటే పై సమీకరణం మొదటి తొమ్మిది దశాంశ స్థానాల వరకు చెల్లింది! ఫెర్మా సమీకరణం చెల్లిపోయిందని హోమర్ సింప్సన్ రుజువు చేసేసేడన్న వార్తతో దేశం అంతా పొక్కిపోయింది.

ఇదే కథాస్రవంతిలో, The Wizard of Evergreen Terrace అనే మకుటంతో ఉన్న మరొక ఉదంతంలో, నేపథ్యంలో ఉన్న ఒక నల్లబల్ల మీద 3787¹² + 4365¹² = 4472¹² అనే సమీకరణం కనబడుతుంది! ఈ సమీకరణం మొదటి పది దశాంశ స్థానాల వరకు చెల్లడమే కాకుండా, సరి చూడడానికి తేలిక అయిన చివరి (ఒకట్ల) స్థానంలో ఉన్న అంకె కూడ సరిపోయింది!

(సింప్సన్స్ టివి సీరియల్‌లో దాగి ఉన్న గణిత సూత్రాల గురించి సైమన్ సింగ్ ఒక పుస్తకం కూడా రాసేడు. ఆ పుస్తకం గురించిన చక్కటి పరిచయం ఈమాటలో వివరంగా వేలూరి వేంకటేశ్వర రావు చేసేడు.)

చివరికి విద్యావంతులలో ఎంతో ఆదరణ పొందిన స్టార్ ట్రెక్ (Star Trek: The Next Generation) అనే కథాస్రవంతిలో, The Royale అనే మకుటంతో ఉన్న ఉదంతంలో కథానాయకుడు, కెప్టెన్ పికార్డ్ – ‘ఫెర్మా చివరి సమస్యని గురించి ఆలోచిస్తూ ఉంటే మనస్సుకి కల్లోలం లేకుండా విశ్రాంతిగా ఉంటుంది,’ అంటాడు.

ఈ వ్యాసం చదివిన పాఠకుల మనస్సు కూడ కల్లోలం లేకుండా విశ్రాంతిగా, ఉల్లాసంగా ఉండాలని కోరుకుంటూ…

ఉపసంహారం

ఈ వ్యాసం చదివిన తరువాత ఈ ప్రయత్నం అంతా కంచి గరుడ సేవ అని కొందరికి అనిపించవచ్చు. గణితం అంతా అర్థం కాకపోయినా మొదటి నుండి చివరికంటా చదివితే కొన్ని విషయాలు మన అవగాహన లోకి వస్తాయి: ఒకటి, శాస్త్రంలో గణితం ఒక ప్రత్యేకమైన శాఖ. ఇది అందరికీ అబ్బదు. అబ్బిన బహు కొద్దిమంది వివరించి చెప్పడానికి ప్రయత్నించినా పరిభాష అర్థం అవదు. భగవద్గీత స్వాములారు చెపుతూ ఉన్నా అర్థం కాదు; అయినా దానిని పారాయణ చేస్తూనే ఉంటాము. అలాగే ఇదీను. పరిశ్రమ చెయ్యగా చెయ్యగా మనకి కూడ కొంతకాకపోతే కొంతైనా అర్థం అవుతుంది. కనుక ప్రయత్నం మానకండి. అప్పుడప్పుడు, అక్కడక్కడ ఏ రామానుజన్ లాంటి వ్యక్తి అయినా తారసపడితే వారి ప్రతిభకి ఒక నమస్కారం పెట్టండి.

(ఈ వ్యాసాన్ని ఎంతో శ్రమతో నిశితంగా సమీక్షించి విలువైన సూచనలు చేసిన పిడూరి రాజాగారికి కృతజ్ఞతలు.)

సంప్రదించిన మూలాలు

1. Simon Singh, Fermat’s Enigma: The epic quest to solve the world’s Greatest Mathematical Problem, Anchor Books, 1997, ISBN: 0-385-49362-2
2. Simon Singh, Fermat’s Last Theorem. Harper Perennial, London, 1997, pp 232-249, ISBN 13 978-1-84115-791-7
3. Fermat’s Last Theorem
4. Michael D. Hirschhorn, Ramanujan and Fermat’s Last Theorem, The Australian Mathematical Society Gazette 01/2004; 31(4).
5. S. Ramanujan, The Lost Notebook and Other Unpublished Papers, Narosa, Delhi, 1988, 341.
6. Robert C. Rhoades, ELLIPTIC CURVES AND MODULAR FORMS, Based on A Course, MATH 844, at the University of Wisconsin – Madison, taught by Professor Nigel Boston, August 10, 2006.
7. వేమూరి నిఘంటువు (ఇంగ్లీషు-తెలుగు).