ఉద్దేశము

ఈ వ్యాసములో మూడు విషయములను చర్చిస్తాను. అవి:

1. అందఱికి పరిచితమైన సులభసూత్రము యమతారాజభానసలగం యందలి గణితాంశములు,
2. వృత్తముల యందలి గణములతో వృత్త సంఖ్యను కనుగొను విధానము,
3. ఎనిమిది త్రిక గణములకు గల గణితవర్గపు లక్షణములు.

యమాతారాజభానసలగం

పింగళ ఛందస్సులోని[1] మొదటి కొన్ని సూత్రములు ఇలాగున్నాయి:

UUU 0 ధీశ్రీస్త్రీం మ్ – (1)
IUU 1 వరా సా య్ – (2)
UIU 2 కా గుహా ర్ – (3)
IIU 3 వసుధా స్ – (4)
UUI 4 సా తే క్వ త్ – (5)
IUI 5 కదా స జ్ – (6)
UII 6 కిం వద భ్ – (7)
III 7 న హస న్ – (8)

ఈ సూత్రములు మూడక్షరముల ఎనిమిది గణములను ఉదాహరణములతో తెలుపుతాయి. ఎనిమిది త్రిక గణములను ఈ విధముగా పింగళుడు ఎందులకు అమర్చినాడు? వసుధా స్, అనగా, స-గణము ఎందుకు మొదటి గణముగా నుండరాదు? గురువుకు విలువ సున్న, లఘువుకు విలువ ఒకటి. ఎక్కువ విలువ ఉండే అంకెలు (most significant digits) కుడివైపు, తక్కువ విలువ ఉండే అంకెలు (least significant digits) ఎడమవైపు ఉపయోగించుట పూర్వకాలములో వాడుక, ఇది నేటి వాడుకకు భిన్నము. ఈ విలువలను ఉపయోగిస్తే మనకు గణములకు అంకెల విలువలు లభిస్తాయి. పై సూత్రములలో వాటిని కూడ నేను చూపినాను. గణములను ఈ విధముగా ఎంందుకు చూపినాడో అనే విషయము మనకు ఇప్పుడు అర్థమవుతుంది. సున్న నుండి ఏడు వఱకు విలువలు ఉండే విధముగా గణములను అమర్చినాడు పింగళుడు. తఱువాతి ప్రశ్న – గణములకు ఈ పేరులే ఎందుకు పెట్టాలి? యాదృచ్ఛికముగా కొన్ని అక్షరములను ఉపయోగించినాడా లేక అంతకంటే ఎక్కువగా అర్థము ఇందులో నున్నదా? నా ఉద్దేశములో ఈ మ/య/ర/స/త/జ/భ/న అక్షరాలు సున్న నుండి ఏడు వఱకు అంకెలను సూచిస్తాయి. అక్షరాలను, ఒత్తులను అంకెలుగా వాడడము మనము ఇప్పుడు కూడ భారతీయ భాషలలో చుస్తున్నాము కదా? కాని దీనికి నావద్ద ఉపపత్తులు ఏమియు లేవు, కేవలము ఊహాగానము మాత్రమే! కాని ఒక విషయము మాత్రము నిజము, ఈ విధముగా సూత్రములను వ్రాసినప్పుడు అతనికి యుగ్మ గణిత సిద్ధాంతములు తెలిసి ఉండాలి. ఇలా తఱువాతి లాక్షణికులు, వ్యాఖ్యలు వ్రాసినవారు చేసినారా అనే ప్రశ్నను కూడ మఱువ రాదు.

ఈ సులభసూత్రమును పాణిని కనుగొన్నాడా?

తెలుగు, కన్నడము, హిందీ, మరాఠీ మున్నగు భాషలలో గణములను జ్ఞాపకములో ఉంచుకొనడానికి య-మా-తా-రా-జ-భా-న-స-ల-గం అనే ఒక సులభసూత్రము వ్యాప్తిలో నున్నది. ఛందస్సు నేర్చుకొనే విద్యార్థికి ఇది తెలిసిన విషయమే. య-మా-తా-రా-జ-భా-న-స-ల-గం సూత్రముపైన బ్రవును ఇలాగంటాడు[2]: The letters used as names of the prosodial feet were selected at an early age, and have been in use throughout India for three thousand years at least. They are combined in an ancient line written by Panini య-మా-తా-రా-జ-భా-న-స-ల-గం. ఇందులో యమాతా య-గణమును, మాతారా మ-గణమును, తారాజ త-గణమును, రాజభా ర-గణమును, జభాన జ-గణమును, నసల న-గణమును, సలగం స-గణమును తెలుపుతాయి. గణము యొక్క పేరు ముందే ఉండడము వలన అందులోని గురు లఘువులను తెలిసికొనుట సులభము అవుతుంది. పాణినికి, య-మా-తా-రా-జ-భా-న-స-లగం సూత్రానికి సంబంధము ఉన్నట్లు నాకు తోచలేదు, ఎందుకంటే మఱెవ్వరు అలా చెప్పలేదు.

సూత్రము వెనుక గల గణితాంశములు

అసలు ఈ సూత్రము ఎలా కనిపెట్టారు? ఇట్టి సూత్రము ఇదొక్కటేనా?

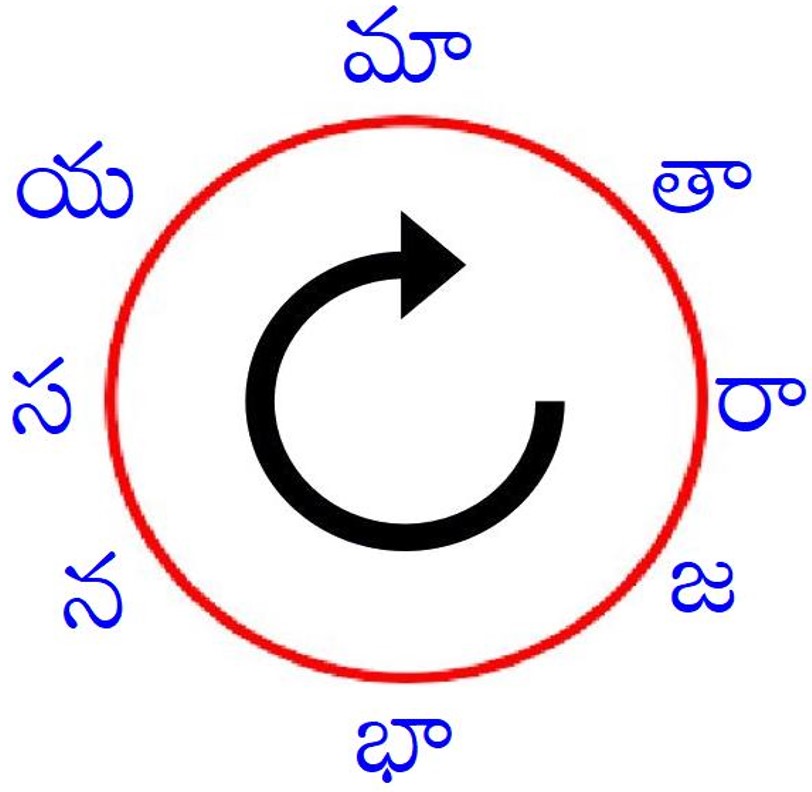
సౌలభ్యమునకై మ-గణముతో ప్రారంభిద్దాము. మ-గణమునకు మూడు గురువులు, కావున మ-గణముతో చేర్చి మూడక్షరములు గురువుగా ఉండాలి. ఇప్పుడు మనకు మా-గం-గం లభిస్తుంది (గం=గురువు, ల=లఘువు). రెండు గురువులతో ప్రారంభమయ్యే మూడక్షరముల గణములు మ-గణము, త-గణము. మ-గణమును మనము ఉపయోగించడమైనది కాబట్టి రెండవ అక్షరము తా. ఏ అమరికలోనైనా ఈ మాతా అక్షరములు పక్కపక్కన ఉండాలి. ఇప్పుడు సూత్రము మా-తా-గం-ల. గణములలో గురులఘువులతో ప్రారంభమయ్యే గణములు రెండు, అవి ర-గణము, భ-గణము. ఇప్పుడు మనకు ఒక చిక్కు. ర-గణమును తీసికొనడమా, భ-గణమును తీసికొనడమా? యమాతా సూత్రములో ర-గణమును తీసికొన్నారు, మనము కూడ అలాగే చేద్దాము. ప్రస్తుతము మన సూత్రము మా-తా-రా-ల-గం. లగముతో ప్రారంభమయ్యే గణములు రెండు, అవి య-గణము, జ-గణము. య అక్షరము ఎప్పుడు మా-తా ముందు ఉండాలి. మా-తా అక్షరాలను ముందే ఉపయోగించినాము, కావున జ-గణమును ఎన్నుకోవాలి. ప్రస్తుతము మన సూత్రము మా-తా-రా-జ-గం-ల. గురువుతో ప్రారంభమయ్యే గణములు నాలుగు – మ, ర, త, భ గణములు. మొదటి మూడింటిని మనము ఉపయోగించినాము, కాబట్టి తఱువాతి అక్షరము భా. మన సూత్రము – మా-తా-రా-జ-భా-ల-ల. రెండు లఘువులతో ప్రారంభమయ్యే గణములు న-గణము, స-గణము. అనగా తఱువాతి అక్షరములు స న యా లేక న స య. య- దీర్ఘముగా నుండుటకు వీలు కాదు, కావున న-స-య సరియైన అమరిక. ఇప్పుడు సూత్రము మా-తా-రా-జ-భా-న-స-య. వర్తులాకారములో ఉంచితే ఈ అమరిక చాలు. ఏ అక్షరము నుండి ప్రారంభించినా అన్ని గణములు మనకు లభిస్తాయి, ఉదా. రా-జ-భా-న-స-య-మా-తా (రా-జ). మొదటి చిత్రమును చూస్తే ఇది చక్కగా బోధ పడుతుంది. రావూరి దొరసామి శర్మ ఇట్టి చిత్రమును[3] ఒక చతురస్రాకారములో చూపియున్నారు.

ఒక సులభసూత్రము కాదు, ఎనిమిది సూత్రాలు.

వర్తులాకారముగా కాక ఒక పంక్తిగా ఈ అమరికను వ్రాయాలంటే అది ఎనిమిది విధములుగా సాధ్యము. ఆ ఎనిమిది పంక్తులు:

1. మా-తా-రా-జ-భా-న-స-య-గం-గం
2. తా-రా-జ-భా-న-స-య-మా-గం-గం
3. రా-జ-భా-న-స-య-మా-తా-గం-ల
4. జ-భా-న-స-య-మా-తా-రా-ల-గం
5. భా-న-స-య-మా-తా-రా-జ-గం-ల
6. న-స-య-మా-తా-రా-జ-భా-ల-ల
7. స-య-మా-తా-రా-జ-భా-న-ల-ల
8. య-మా-తా-రా-జ-భా-న-స-ల-గం

ఇప్పుడు చూడండి, య-మా-తా-రా-జ-భా-న-స-ల-గం అమరికలో ప్రత్యేకత ఏమియు లేదు. మొత్తము ఇలాటివి ఎనిమిది ఉన్నాయి. అందులో రెండు ల-గం తోను, రెండు ల-ల తోను, రెండు గం-ల తోను, రెండు గం-గం తోను, అంతమవుతాయి. ఈ ఎనిమిదింటిలో ఏదో ఒకదానిని ఎన్నుకోవాలి. బహుశా యమాతా-ను ఎన్నుకొన్నారని నా భావన.

ఇంకొక సులభసూత్రము

తఱువాతి ప్రశ్న – ఒక్క సులభ సూత్రమేనా, ఇంకా ఉన్నాయా?

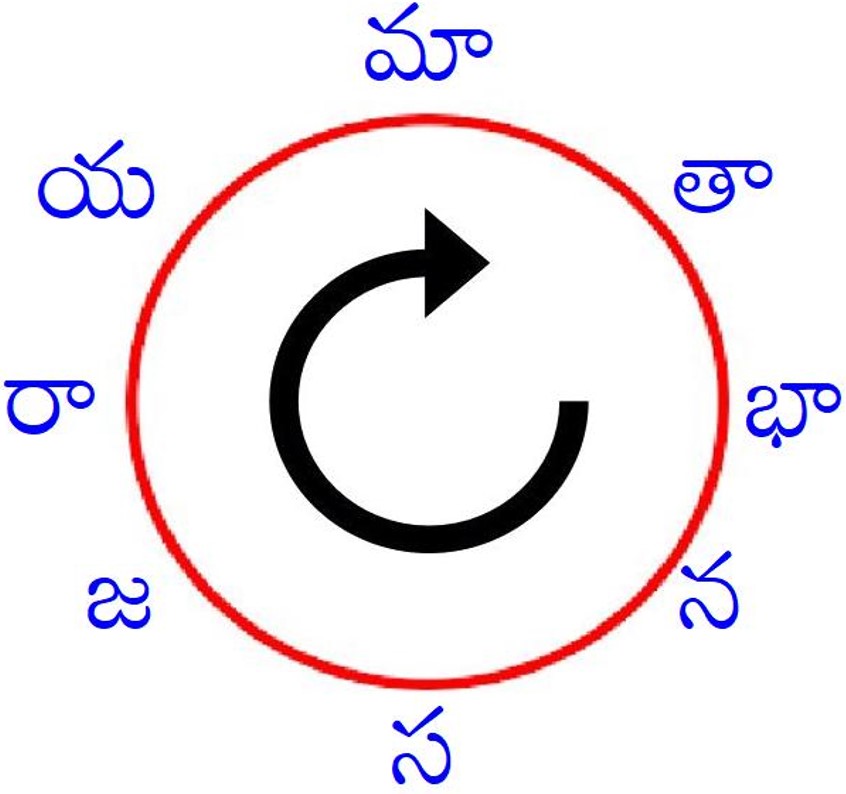
పై వివరణలో నేను మాతా తఱువాత భ-గణమును కూడ ఎన్నుకొన వచ్చునని చెప్పినాను కదా? అలా చేస్తే మనకు మఱొక సులభసూత్రము లభిస్తుంది. అందులోని సోపానపంక్తులను ఔత్సాహికులకు వదలి జవాబును మీకు ఇస్తున్నాను. అది – మా-తా-భా-న-స-జ-రా-య. దీనిని నేను సుమారు పది సంవత్సరాలకు ముందు కనుగొన్నాను. దీనిని కూడ వర్తులాకారముగా అమర్చ వీలగును (రెండవ చిత్రము). మాతాభా మ-గణము, తాభాన త-గణము, భానస భ-గణము, నసజ న-గణము, సజరా స-గణము, జరాయ జ-గణము, రాయమా ర-గణము, యమాతా య-గణము. నేరుగా పంక్తి రూపములో వ్రాయలంటే, యమాతావలెనే దీనినికూడ ఎనిమిది విధములుగా వ్రాయవచ్చును, అవి:

1. మా-తా-భా-న-స-జ-రా-య-గం-గం
2. తా-భా-న-స-జ-రా-య-మా-గం-గం
3. భా-న-స-జ-రా-య-మా-తా-గం-ల
4. న-స-జ-రా-య-మా-తా-భా-ల-ల
5. స-జ-రా-య-మా-తా-భా-న-ల-ల
6. జ-రా-య-మా-తా-భా-న-స-ల-గం
7. రా-య-మా-తా-భా-న-స-జ-గం-ల
8. య-మా-తా-భా-న-స-జ-రా-ల- గం

ఈ ఎనిమిది అమరికలలో కూడ రెండు ల-గం తో, రెండు ల-ల తోను, రెండు గం-ల తోను, రెండు గం-గం తోను, అంతమవుతాయి.

రెండు సూత్రములకు గల సంబంధము

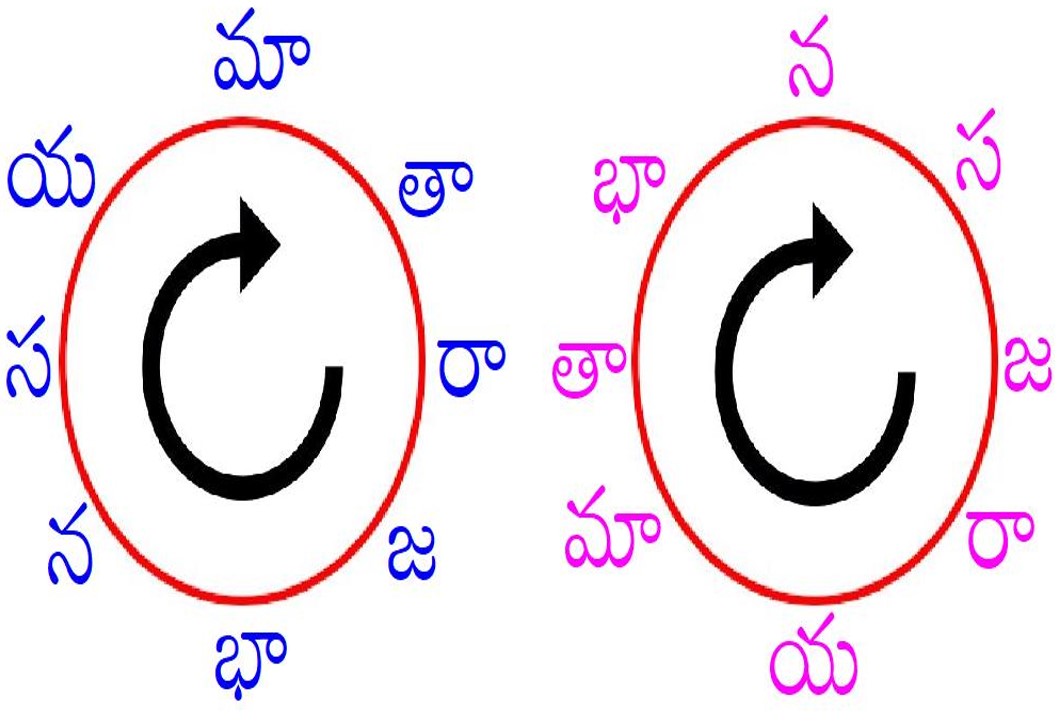
ఈ రెండవ చిత్రమును అపసవ్యముగా 135 డిగ్రీలు త్రిప్పుదామా? అప్పుడు మనకు మూడవ చిత్రములోని కుడివైపు అమరిక దొఱుకుతుంది. మూడవ చిత్రములో ఎడమవైపు అమరిక మొదటి చిత్రములో వలెనే ఉన్నది. ఇప్పుడు ఈ రెండు చిత్రములను జాగ్రత్తగా పరీక్షిస్తే మనకు ఒక విషయము స్పష్టమవుతుంది. రెండు చిత్రములను పంక్తులుగా క్రింద వ్రాద్దామా? గురులఘువులు, వాటి విలువలను కూడ ఇచ్చినాను.

1. మా-తా-రా-జ-భా-న-స-య – UUUIUIII 00010111
2. న-స-జ-రా-య-మా-తా-భా – IIIUIUUU 11101000

ఇలా వ్రాసినప్పుడు మొదటి పంక్తిలో గురువులు ఉన్న చోటులలో రెండవ పంక్తిలో లఘువులు కనబడుతాయి. ఈ విధమైన అమరికలో ఎనిమిది జంట గణములు ఇలాగున్నాయి – మ-న, త-స, ర-జ, జ-ర,భ-య, న-మ, స-త, య-భ. ఈ జంట గణముల ప్రత్యేకత ఏమనగా వాటిలో గురు-లఘువులు తారుమారయ్యాయి, ఉదా. భ (UII), య (IUU). ఫోటాగ్రఫీలో పాజిటివ్ – నెగెటివ్ వంటిది ఇది.

రెండు అమరికలు మాత్రమే

చివరి ప్రశ్న – ఈ రెండు అమరికలేనా, ఇంకా ఉన్నాయా?

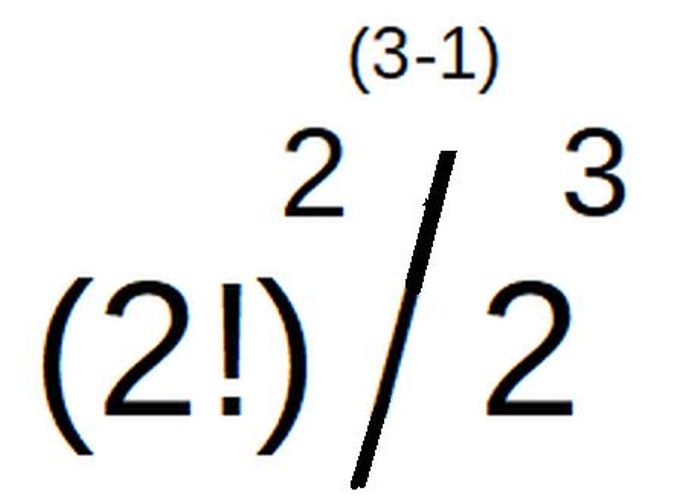
ఈ సులభసూత్రములు గణితశాస్త్రములో డె బ్రుయిన్ వరుసకు (de Bruijn sequence) చాల పురాతనమైన ఉదాహరణము. నిడివి 3 (గణములలోని అక్షరముల సంఖ్య), అక్షరములు రెండు (గురువు, లఘువు లేక 1, 0). ఈ వర్తులమైన అమరిక పొడవు 2³, అనగా 8. ఇట్టివి మొత్తము [(2!)^(2^(3-1))] / [2^3]. దీని విలువ 2⁴/2³ = 2. అనగా ఇట్టి వరుసలు రెండు మాత్రమే. మా-తా-రా-జ-భా-న-స-య (00010111) మఱియు న-స-జ-రా-య-మా-తా-భా (11101000) మాత్రమే సాధ్యము. రెండింటి ప్రత్యేకత గురులఘువుల స్థానములయందలి మార్పు.

ఈ త్రిక గణములను గుఱించిన మఱి కొన్ని విశేషాలు, వాటితో కల్పించిన కొన్ని వృత్తాలు అనుబంధములో నేను జతపఱచినాను.

గణములనుండి వృత్త సంఖ్య

సామాన్యముగా వృత్త సంఖ్యను గురులఘువుల వరుసనుండి నిర్ణయిస్తారు. దీనికి ఉద్దిష్టము అని పేరు. తనుమధ్యా వృత్తమునకు గురు లఘువులు – UUIIUU. గురువుకు సున్న, లఘువుకు ఒకటి ఉంచితే, దీని యుగ్మాంకము 001100. ఈ యుగ్మాంకము దశాంశములో ఇలా వ్రాయవచ్చును: 0.1 + 0.2 + 1.4 + 1.8 + 0.16 + 0.32 = 12. దీనికి ఒకటి చేరిస్తే ఆఱు అక్షరములు ఉండే గాయత్రీ ఛందస్సులో ఈ వృత్తపు సంఖ్య 13. ఈ వృత్తపు గణములు త/య. వృత్తపు గణములతో కూడ ఈ సంఖ్యను కనుగొన వీలగును. కాని ఈ విషయము నేను ఇంతవఱకు ఎక్కడ చదువలేదు. క్రింద దానిని వివరిస్తున్నాను.

గురులఘువులతో వృత్త సంఖ్యను కనుగొనుటకు యుగ్మాంక గణితమును (binary arithmetic) ఉపయోగిస్తాము. గణములతో కనుగొనుటకు అష్టాంక గణితము (octal arithmetic) ఉపయోగించాలి. గణపు విలువలు (మ-గణాదులు), గణ స్థానపు విలువలు (ఒకటవ, రెండవ, మున్నగు గణములు) మనము తెలిసికోవాలి. అవి క్రింద ఇవ్వబడినవి.

గణముల విలువలు – 0 మ, 1 య, 2 ర , 3 స, 4 త , 5 జ, 6 భ, 7 న.

గణ స్థానపు విలువలు – 1 – 1 , 2 – 8, 3 – 64 , 4 – 512, 5 – 4096, 6 – 32768, 7 – 262144, 8 – 2097152 , 9 – 16777216.
గణము అసంపూర్ణముగా ఉన్నప్పుడు ప్రక్కన గురువు(లు) చేర్చుకొని త్రిక గణముగా మార్చుకొనవలయును. గురువు విలువ సున్న కనుక దీని వలన ఏ ఇబ్బంది లేదు. ఉదా. లగము ఉంటే, దానిని య-గణముగా మార్చుకోవాలి. క్రింద కొన్ని ఉదాహరణములు:

• తనుమధ్యా – త/య
  4.1 + 1.8 = 12, దీనికి ఒకటి చేరిస్తే వృత్త సంఖ్య 13.
• తోటకము – స/స/స/స (స-గణపు విలువ = 3)
  3.1 + 3.8 + 3.64 + 3.512 = 1755, దీనికి ఒకటి చేర్చినప్పుడు మనకు వృత్త సంఖ్య 1756 లభించును. తోటక వృత్త సంఖ్య 1756.
• శార్దూలవిక్రీడితము – మ/స/జ/స/త/త/గ
  చివరి గణము అసంపూర్ణము, దానికి రెండు గురువులు కుడి ప్రక్కన తగిలిస్తే అది మ-గణము అవుతుంది.
  0.1 + 3.8 + 5.64 + 3.512 + 4.4096 + 4.32768 + 0.262144 = 149336. దీనికి 1 చేరిస్తే 149337 వస్తుంది. శార్దూలవిక్రీడితపు వృత్త సంఖ్య 149337.
• మంగళమహాశ్రీ – భ/జ/స/న/భ/జ/స/న/గగ
  చివరి అసంపూర్ణ గణమునకు గురువు చేరిస్తే అది మ-గణము అవుతుంది.
  6.1 + 5.8 + 3.64 + 7.512 + 6.4096 + 5.32768 + 3.262144 + 7.2097152 + 0.16772216 = 15658734. దీనికి 1 చేరిస్తే 15658735 లభిస్తుంది. మంగళమహాశ్రీ వృత్త సంఖ్య 15658735.

ఎనిమిది త్రిక గణములతో ఒక గణితవర్గము

ఎనిమిది త్రిక గణములు ఒక గణిత వర్గమునకు చెందినవని ఇప్పుడు నిరూపిస్తాను. గణితశాస్త్రములో వర్గము (group) అంటే కొన్ని అంశముల (elements) సముదాయము. రెండు అంశములపైన ఒక వర్గ ప్రక్రియను (group operation indicated by a dot) ఉపయోగిస్తే మనకు లభించే ఆ మూడవ అంశము ఆ సముదాయములో తప్పక ఉండి తీరాలి. ఉదాహరణముగా అంశముల సముదాయము పూర్ణాంకములుగా (whole numbers) నుండవచ్చును; ప్రక్రియ కూడికగా (addition) నుండవచ్చును. 1+2 అంటే మనకు లభించే 3 ఆ సముదాయములోనే ఉన్నది. దీనినే ఆవరణము (closure) అంటారు. అంతే కాక (a.b).c = a.(b.c), ఉదాహరణముగా (1 + 2) + 3 = 1 + (2 + 3) = 6. దీనిని సహయోగ సిద్ధాంతము (associative law) అంటారు. సముదాయములో ఒక ప్రత్యేక అంశము (identity element) ఉంటుంది. దీని ప్రత్యేకత ఏమనగా ఈ అంశముతో ఏ అంశముపైన ప్రక్రియ జరిగినను, అదే అంశము సిద్ధిస్తుంది. ఉదా. పూర్ణాంకములలో శూన్యము ఒక ప్రత్యేకాంశము. 0+1 = 1; 0+2 = 2, ఇత్యాదులు. ప్రతి అంశమునకు ఒక విలోమాంశము (inverse) ఉంటుంది. అంశ విలోమాంశముల ప్రక్రియ ఫలితము ప్రత్యేక అంశముగా ఉంటుంది. ఉదా. సంఖ్య ఒకటికి విలోమము -1, 1 + (-1) = 0. ఇవి వర్గ సిద్ధాంతములు. a.b ఎల్లప్పుడు b.a కాదు. ఉదాహరణముగా వర్గ ప్రక్రియ భాగహారమయితే, 2/3, 3/2 కాదు కదా? a.b = b.a అయితే ఆ వర్గమును అబీలియన్ వర్గము (Abelian category) అంటారు. కావున గణిత వర్గమునకు ముఖ్యమైనవి: అంశముల సముదాయము (group of elements), ఆవరణము (closure), సహయోగము (associativity), ప్రత్యేక అంశము (identity element), విలోమాంశము (inverse).

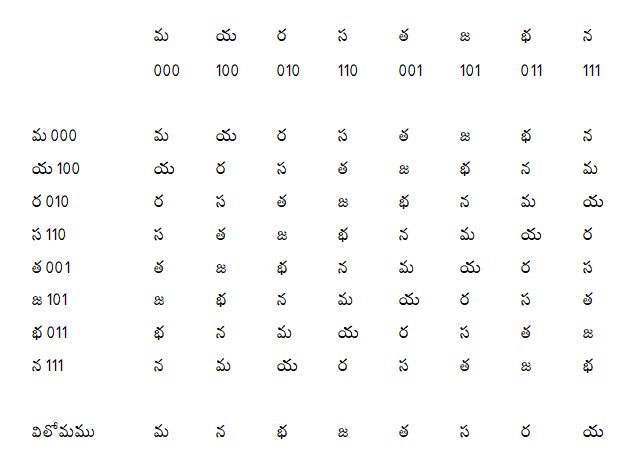
మ, య, ర, స, త , జ, భ, న, గణములను వాటి యుగ్మాంకముల ద్వారా మనము తెలిపితే, వర్గ ప్రక్రియగా కూడికను తీసికొంటే ఈ త్రిక గణములను ఒక గణిత వర్గముగా భావించ వీలగును. ఈ గణిత వర్గపు గుణకార పట్టికను నాలుగవ చిత్రములో చూడవచ్చును. కూడిక ఫలితము ఏడుకన్న ఎక్కువగా ఉంటే, దానినుండి ఎనిమిదిని తీసివేయాలి. ఇందులో ప్రతి పంక్తిలో ఈ ఎనిమిది గణములు తప్ప మఱే గణములు లేవు. కావున ఇది ఆవరణ సిద్ధంతమును (closure) నిరూపిస్తుంది. ఈ పట్టికలో (a.b).c = a.(b.c). ఉదాహరణముగా (స.జ).న = మ.న = న; స.(జ.న) = స.త = న. ఇది సహయోగమును (associativity) నిరూపిస్తుంది. మ-గణము (000) ప్రత్యేక అంశము (identity element). దీనితో కూడిక ప్రక్రియ చేయగా అదే గణము దొరుకుతుంది. అందుకే పట్టికలోని మొదటి పంక్తిలో ఏ మార్పు లేదు. ప్రతి అంశమునకు ఒక విలోమము (inverse) ఉన్నది. అది చివరి పంక్తిలో చూపబడినది. ఒక అంశమును దాని విలోమముతో ప్రక్రియ చేయగా మనకు ప్రత్యేక అంశము లభించును, ఉదాహరణమునకు త.త (త యొక్క విలోమము) = మ; న.య (న యొక్క విలోమము) = మ. ఈ పట్టికనుండి a.b = b.a అని గమనించ వచ్చును, ఉదాహరణమునకు జ.ర = ర.జ = న. అందువలన ఈ వర్గము అబీలియన్ వర్గము (Abelian group). ఛందస్సులో ఉపయోగించే ఎనిమిది త్రిక గణములైన మ, య, ర, స, త, జ, భ, న గణములు వాటి యుగ్మాంకముల ద్వారా కూడిక ప్రక్రియలో ఒక గణితవర్గము అవుతుందని ఇందువలన నిరూపించడమైనది.

గ్రంథసూచి

1. ఛందఃశాస్త్రం, శ్రీపింగలనాగ – సంపాదకుడు పండిత కేదారనాథ, Parimal Publications, Delhi 1994 . పుటలు 2-4.
2. Sanskrit Prosody and Numerical Symbols Explained – Charles Philip Brown, Trubner and Co., London, 1869. Appendix, page 28.
3. తెలుగు భాషలో ఛందోరీతులు – రావూరి దొరసామిశర్మ, వెల్డన్ ప్రెస్, మదరాసు, 1962. పుట 41.