పరిచయము

సంస్కృత ఛందస్సు నియమములను అనుసరిస్తూ మిగిలిన భారతీయ భాషలు తమదైన ఛందస్సును సృష్టించుకొన్నాయి. కాని ఆయా భాషల అవసరాన్ని బట్టి మార్పులు కూడ జరిగాయి. సంస్కృతము, ప్రాకృతము, కన్నడ-తెలుగు ఛందస్సులు ఇట్టివే. వీటికి సమాంతరముగా తమిళ భాష సంస్కృతపు ప్రభావము లేకుండా ఒక కొత్త ఛందస్సును ఏర్పరచుకొన్నది. ఈ ఛందస్సులలో ఉండే గణితశాస్త్రపు సిద్ధాంతములను వివరించడమే ఈ వ్యాసపు ముఖ్యోద్దేశము. ఈ సందర్భములో ఇంతకు ముందే ఎన్నో విషయములను చర్చించాను. ఆ వ్యాసములోని కొన్ని అంశములను చిత్రములతో వివరిస్తాను. తమిళ ఛందస్సులోని గణితాంశములను మొట్టమొదటిసారిగా చర్చిస్తాను. ఈ ప్రయత్నము ఇంతవఱకు ఎవ్వరు చేయలేదు. అంతే కాక సంస్కృత, తమిళ, కన్నడ-తెలుగు ఛందస్సు పద్ధతులనన్నిటిని చేర్చుకొన్న ఒక కొత్త విధానమును కూడ సూచిస్తాను.

సంస్కృత ఛందస్సు

1. సంస్కృత గణోత్పత్తి

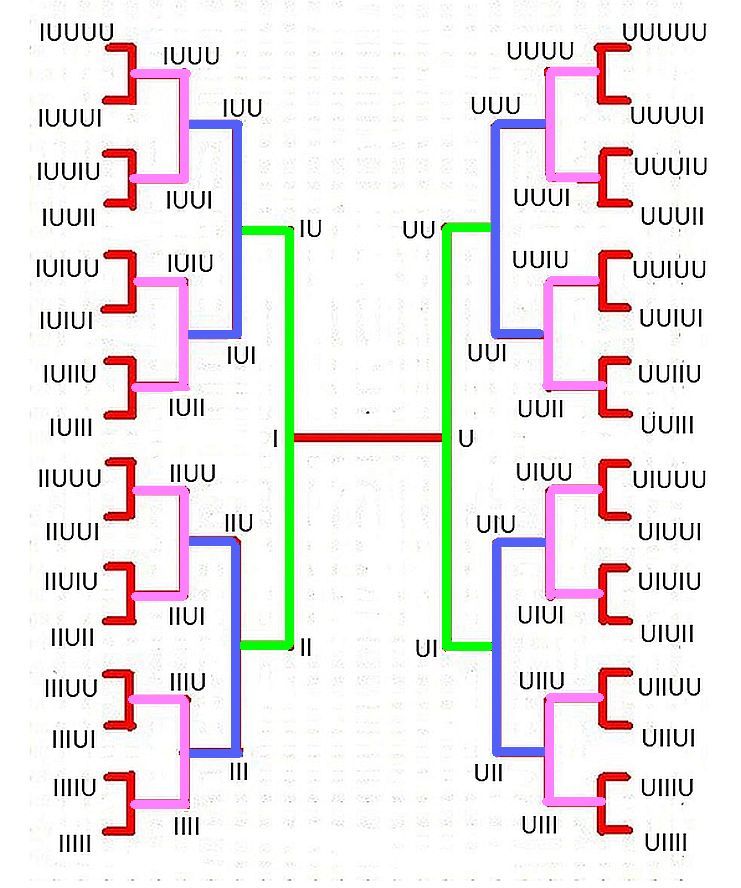
సంస్కృత ఛందస్సు పునాది గురు (U) లఘువులు (I). ఈ గురు లఘువులకు పదేపదే గురు లఘువులను చేర్చినప్పుడు మనకు గణములు, వృత్తములు లభిస్తాయి. పద్యములో పాదములు ఉంటాయి, పాదములో ఒక నియమిత సంఖ్య గల అక్షరములు ఉంటాయి, ఈ అక్షరములను సౌలభ్యమునకై కొన్ని గణములుగా విభజిస్తారు, ఈ గణములు గురు లఘువుల సముదాయము. అనగా పద్యమంతా గురులఘువులతో నిండి ఉంటుంది. ఒక అక్షరము తప్పనిసరిగా ఒక గురువుగానో లేక లఘువుగానో ఉండాలి. అందువలన ఈ గణితము యుగ్మాంక గణితమును (binary arithmetic) అనుసరిస్తుంది. గణోత్పత్తిని గుఱించిన వివరాలు మొదటి చిత్రములో ఇవ్వబడినాయి. దీనిని గణవృక్షము అని చెప్పవచ్చును. ఇందులో కుడివైపు ఉండే గణములు గురువుతో ఆరంభమవుతాయి, ఎడమవైపు ఉండే గణములకు లఘువు మొదటి అక్షరముగా ఉంటుంది. ఆకుపచ్చని గీతల కొనలలో రెండక్షరముల గణములను, వంగపండు రంగు గీతల కొనలలో మూడు అక్షరముల గణములను, గులాబి రంగు గీతల కొనలలో నాలుగు అక్షరముల గణములను, ఎఱ్ఱ రంగు గీతల కొనలలో ఐదు అక్షరముల గణములను (లేక వృత్తములను) చూపినాను. ఏకాక్షర గణములు రెండైతే, రెండక్షరముల గణములు నాలుగు, మూడక్షరముల గణములు ఎనిమిది, ఇలా అక్షరముల సంఖ్య ఒకటి హెచ్చవగా గణముల సంఖ్య ద్విగుణీకృతము అవుతుంది. ఈ సంఖ్యలైన 2, 4, 8, 16, 32, … అమరికను ఒక గుణ (గుణాంక) శ్రేఢిగా (geometric progression) పరిగణించవచ్చును. ఈ శ్రేణికి సామాన్య నిష్పత్తి (common ratio) 2. లగారంభమై (IU) ఎదురు నడకతో సాగే గణములు చిత్రములోని వాయవ్య భాగములో (ఎడమ ఉపరిభాగము) ఉన్నాయి. ఒక పాదములో ఒక నియమిత సంఖ్యగల గురు లఘువుల అమరికలు ఎన్ని ఉన్నాయో అన్న విషయము యుగ్మ సిద్ధాంతము (binomial theorem) తెలుపుతుంది. ఈ సమాచారమును గణ మేరువు (Pascal triangle) ద్వారా కూడ మనము తెలిసికొన వీలగును. ఈ విషయములను ఇదే పేరితో ఉండే వ్యాసపు మొదటి భాగములో చర్చించాను.

మాత్రా ఛందస్సు

సంస్కృత ఛందస్సు అక్షర సంఖ్యపైన ఆధారపడి ఉంటే ప్రాకృతములో మాత్రాఛందస్సుకే పెద్ద పీట. ఎందుకంటే అట్టివి పాడుకోడానికి అనువుగా ఉంటుంది. ఒక మాత్ర లేక కళ అంటే ఒక హ్రస్వాక్షరమును ఉచ్చరించే కాలావధి. లఘువును ఒక మాత్రగా, గురువును రెండు మాత్రలుగా పరిగణిస్తారు. మాత్రల సంఖ్య ఎక్కువయినప్పుడు మాత్రాగణముల సంఖ్య కూడ ఎక్కువ అవుతుంది. ఈ మాత్రాగణముల సంఖ్యను విరహాంకుడు మొట్టమొదట కనుగొన్నాడు. ఆ మాత్రాగణముల సంఖ్య 1 (ఒక మాత్ర), 2 (రెండు మాత్రలు), 3 (మూడు మాత్రలు), 5 (నాలుగు మాత్రలు), 8 (ఐదు మాత్రలు), 13 (ఆఱు మాత్రలు), … ఈ సంఖ్యలను తఱువాతి లాక్షణికులైన గోపాల, హేమచంద్రులు కూడ చర్చించినారు. ఈ సంఖ్యలను విరహాంక-హేమచంద్ర సంఖ్యలు అని పిలువవలయును. కాని నేడు వాటిని ఫిబొనాచ్చి సంఖ్యలు (Fibonacci numbers) అని పిలుస్తారు. ఈ సంఖ్యల అమరిక లోని కిటుకు ఏమంటే ఒక సంఖ్య విలువ దానికి ముందున్న రెండు అంకెల కూడిక ఫలితం. దీనిని F(n) = F(n-1) + F(n-2) అని వ్రాస్తారు. ఒక పంచభుజిలో (pentagon) వికర్ణపు (diagonal) నిడివిని భుజపు నిడివితో భాగహారము చేసినప్పుడు లభించిన ఫలితమును స్వర్ణ నిష్పత్తి (golden ratio) అని పిలుస్తారు. దీని విలువ φ = (√5 + 1) / 2 = 1.618033… ఇది ఒక కరణీయ సంఖ్య (irrational number.) విరహాంక-హేమచంద్ర సంఖ్యలలో పక్కపక్కన ఉండే అంకెల నిష్పత్తి విలువ సుమారుగా ఈ φ విలువ. అనగా ఈ సంఖ్యలు కూడ ఒక గుణశ్రేఢి అమరికలో సామాన్య నిష్పత్తి φతో ఉంటుంది.

దేశి ఛందస్సు

2. దేశి ఛందస్సు

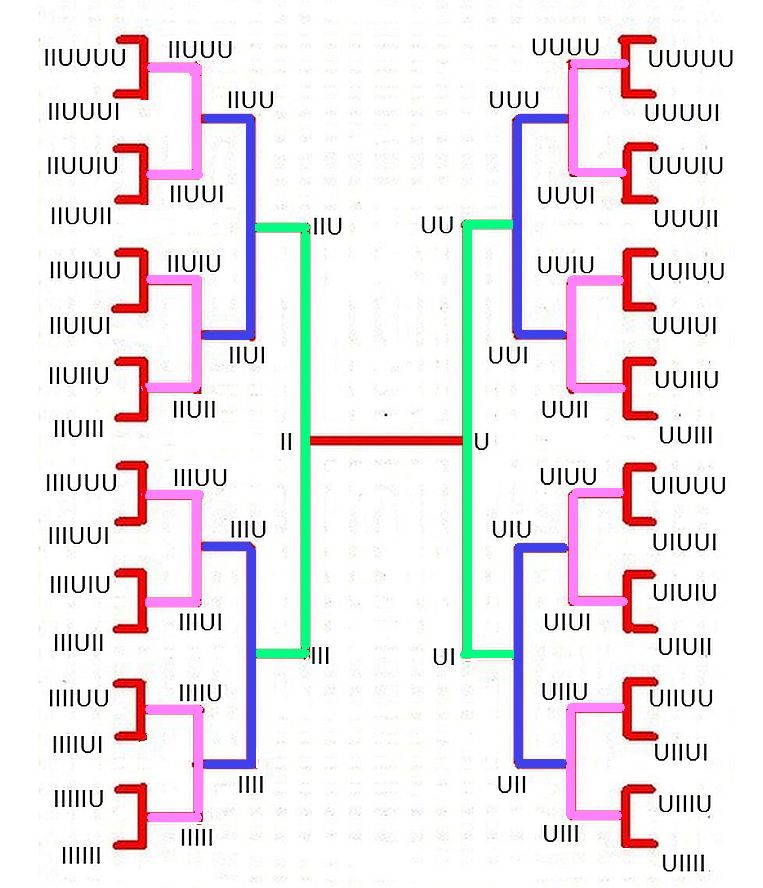
కన్నడ-తెలుగు దేశి ఛందస్సులోని ప్రత్యేకత ఏమంటే వీటిలో ఎదురు నడక, అనగా లగారంభ (IU) గణములు ఉండవు. ఈ ఛందస్సు సంస్కృత ఛందస్సులా పూర్తిగా అక్షర ఛందస్సు కాదు, పూర్తిగా మాత్రా ఛందస్సు కూడా కాదు. రెంటి గుణములను కలిపికొన్నది ఇది. దీనికి పునాది రాళ్ళు అక్షర ఛందస్సులోవలె ఒక గురువు, ఒక లఘువుతో కాక రెండు మాత్రలు, అనగా ఒక గురువు (U), రెండు లఘువులు (II.) వీటితో నిర్మించబడిన గణములను రెండవ చిత్రములోని అంశ లేక ఉపగణ వృక్షములో చూడవచ్చును. ఇందులోని కుడి భాగమునకు, మొదటి చిత్రములోని కుడి భాగమునకు ఎట్టి భేదము లేదు. ఎందుకనగా, రెంండింటిలో ఒక గురువుకు పదేపదే గురు లఘువులను కలిపి కొత్త గణములు సృష్టించబడినాయి. ఎడమపక్కన ఉండే గణములన్ని రెండు లఘువులతో ఆరంభమవుతాయి. మన పునాది రాళ్ళు రెండు మాత్రలు (U, II) కావున ఈ గణముల నిర్మాణములో లగారంభ గణములు ఉండవు, కావున ఎదురు నడక ప్రస్తావన లేదు. ఆకుపచ్చని గీతల కొనలలోని గణములు బ్రహ్మ గణములు, వంగపండు రంగు గీతల కొనలలోని గణములు విష్ణు గణములు, గులాబి రంగు గీతల కొనలలోని గణములు రుద్ర గణములు. ఈ గణములలో చిత్రపు పై భాగములో ఆయా రంగుల కొనలలో ఎదురెదురుగా ఉండే గణములను తొలగించినప్పుడు మనకు తెలుగు దేశి ఛందస్సులోని సూర్య, ఇంద్ర, చంద్ర గణములు లభిస్తాయి. ఈ గణముల అమరికలో కూడ ప్రతి సోపానములోని గణముల సంఖ్య తఱువాతి సోపానములో రెట్టింపు అవుతుంది.ఆందువలన గణముల సంఖ్యలు 2, 4, 8, 16, 32, … ఇత్యాదులు ఒక గుణశ్రేఢి అవుతుంది. ఈ గుణశ్రేఢి సామాన్య నిష్పత్తి కూడా 2. ఈ అంశ లేక ఉపగణములకు కూడ మేరు నిర్మాణము సాధ్యము అవుతుందని ప్రప్రథమముగా ముందటి వ్యాసములో తెలిపినాను.

తమిళ ఛందస్సు

మిగిలిన భారతీయ భాషలలోని ఛందస్సులలో అక్షరపు విలువ గురువు, లఘువు లేదా మాత్రగా పరిగణించబడగా తమిళ లాక్షణికులు తమదైన ఒక నూతన పథమును నిర్మించుకొన్నారు. తమిళ ఛందస్సులోని ఇటుకరాయి అశై (அசை.) అశై అంటే చలనము, ఛందస్సు పరముగా స్వరము అని చెప్పవచ్చును. ఈ అశై రెండు విధములు – నేరశై (நேரசை), నిరైయశై (நிரையசை.) నేరశై అన్నది ఒక గురువు (U) లేక ఒక లఘువు (I) కావచ్చును. తెలుగులో గా, గం, గాన్ ఇవన్నీ గురువులే ఐనా, తమిళములో వీటిని వేఱువేఱుగా పరిగణిస్తారన్న విషయమును ఇక్కడ గుర్తు ఉంచుకోవాలి. నిరైయశై కూడ రెండు విధములు, అవి – II, IU. టేకుమళ్ళ రాజగోపాలరావు నేరశైను గో అనియు నిరైయశైను ధన అని పిల్చినారు[1]. రెంటిని చేర్చినప్పుడు మనకు గోధన అనే పదము లభ్యమవుతుంది. ఆ కాలములో గోవులు ధనమే కదా! నేరశైను – గుర్తుతో, నిరైయశైను = గుర్తుతో కూడ సూచిస్తారు. ఒక అక్షరము కలిగిన స్వరమునకు ఒక అడ్డ గీత, రెండక్షరములు కలిగిన స్వరమునకు రెండు అడ్డ గీతలు అని భావించవచ్చును. తమిళ ఛందస్సులో గణమును శీర్ (சீர்) అంటారు. పదేపదే నేర్ మఱియు నిరై లను కలిపినప్పుడు మనకు తమిళ ఛందస్సులోని గణములు పుట్టుతాయి. ఒక విషయము – నేరశై గణము చివర లఘువుగా నుండవచ్చును కాని గణారంభములో, గణము మధ్య భాగములో, అది ఎప్పుడూ గురువే.

రెండు స్వరముల గణములు నాలుగు రీతులుగా ఉద్భవిస్తాయి, అవి – నేర్-నేర్, నేర్-నిరై, నిరై-నేర్, నిరై-నిరై. ఆ గణములను మొదటి పట్టికలో చూడవచ్చును. అదే విధముగా మూడు స్వరములతో ఎనిమిది విధములైన గణములను కల్పించవచ్చును, అవి – నేర్-నేర్-నేర్, నేర్-నిరై-నిరై, నిరై-నేర్-నిరై, నిరై-నిరై-నేర్, నిరై-నిరై-నిరై, నిరై-నేర్-నేర్, నేర్-నిరై-నేర్, నేర్-నేర్-నిరై. వీటి వివరములను రెండవ పట్టికలో పరిశీలించ వీలగును. అదే విధముగా నాలుగు స్వరములతో కల్పించిన 16 గణములను మూడవ పట్టికలో గమనించవచ్చును.

పట్టిక 1. మా- గణములు, విళం- గణములు

గణము	అశై అమరిక	గో-ధనములు		గురు లఘువుల అమరిక
తేమా	నేర్ – నేర్	గో – గో	– –	UU, UI
పుళిమా	నిరై – నేర్	ధన – గో	= –	IIU, III, IUU, IUI
కూవిళం	నేర్ – నిరై	గో -ధన	– =	UII, UIU
కరువిళం	నిరై – నిరై	ధన – ధన	= =	IIII, IIIU, IUII, IUIU

పట్టిక 2. కాయ్- గణములు, కని- గణములు

గణము	అశై అమరిక	గో-ధనములు		గురు లఘువుల అమరిక
తేమాంగాయ్	నేర్ – నేర్ – నేర్	గో – గో – గో	– – –	UUU, UUI
పుళిమాంగాయ్	నిరై – నేర్ – నేర్	ధన – గో – గో	= – –	IIUU, IUUU, IIUI, IUUI
కరువిళంగాయ్	నిరై – నిరై – నేర్	ధన – ధన- గో	= = –	IIIIU, IUIUU, IIIUU, IUIIU, IIIII, IUIUI, IIIUI, IUIII
కూవిళంగాయ్	నేర్ – నిరై – నేర్	గో – ధన – గో	– = –	UIIU, UIUU, UIII, UIUI
తేమాంగని	నేర్ – నేర్ – నిరై	గో – గో -ధన	– – =	UUII, UUIU
పుళిమాంగని	నిరై – నేర్ – నిరై	ధన – గో – ధన	= – =	IUUIU, IUUII, IIUIU, IIUII
కరువిళంగని	నిరై -నిరై -నిరై	ధన -ధన -ధన	= = =	IIIIII, IIIIIU, IIIUII, IUIIII, IUIUIU, IUIUII, IUIIIU, IIIUIU
కూవిళంగని	నేర్ – నిరై – నిరై	గో – ధన -ధన	– = =	UIIII, UIIIU, UIUII, UIUIU

పట్టిక 3. పూ- గణములు, నిఴల్- గణములు

గణము	అశై అమరిక	గో-ధనములు		గురు లఘువుల అమరిక
తేమాందన్బూ	నే – నే – నే – నే	గో – గో – గో –గో	– – – –	UUUU, UUUI
పుళిమాందన్బూ	ని – నే – నే – నే	ధన – గో – గో – గో	= – – –	IIUUU, IIUUI, IUUUU, IUUUI
కూవిళందన్బూ	నే – ని – నే – నే	గో – ధన – గో –గో	– = – =	UIIUU, UIIUI, UIUUU, UIUUI
కరువిళందన్బూ	ని – ని – నే – నే	ధన – ధన – గో – గో	= = – –	IIIIUU, IIIIUI, IIIUUU, IIIUUI, IUIIUU, IUIIUI, IUIUUU, IUIUUI
తేమానఱునిఴల్	నే – నే – ని – ని	గో – గో – ధన –ధన	– – = =	UUIIII, UUIIIU, UUIUII, UUIUIU
పుళిమానఱునిఴల్	ని – నే – ని – ని	ధన – గో – ధన – ధన	= – = =	IIUIIII, IIUIIIU, IIUIUII, IUUIIII, IUUIUIU, IUUIUII, IUUIIIU, IIUIUIU
కూవిళనఱునిఴల్	నే – ని – ని – ని	గో – ధన – ధన –ధన	– = = =	UIIIIII, UIIIIIU, UIIIUII, UIUIIII, UIUIUIU, UIUIUII, UIUIIIU, UIIIUIU
కరువిళనఱునిఴల్	ని – ని – ని – ని	ధన – ధన – ధన – ధన	= = = =	IIIIIIII, IIIUIIII, IUIIIIII, IUIUIIII,IIIIIUII, IIIUIUII, IUIIIUII, IUIUIUII, IIIIIIIU, IIIUIIIU, IUIIIIIU, IUIUIIIU, IIIIIUIU, IIIUIUIU, IUIIIUIU, IUIUIUIU
తేమానఱుంబూ	నే – నే – ని – నే	గో – గో – ధన -గో	– – = –	UUIIU, UUIUU, UUIII, UUIUI
పుళిమానఱుంబూ	ని – నే – ని – నే	ధన – గో – ధన – గో	= – = –	IIUIIU, IUUIIU, IIUIUU, IUUIUU, IIUIII, IUUIII, IIUIUI, IUUIUI
కరువిళనఱుంబూ	ని – ని – ని – నే	ధన – ధన – ధన – గో	= = = –	IIIIIII, IUIIIII, IIIUIII, IIIIIUI, IUIUIII, IUIIIUI, IIIUIUI, IUIUIUI, IIIIIIU, IUIIIIU, IIIUIIU, IIIIIUU, IUIUIIU, IUIIIUU, IIIUIUU, IUIUIUU
కూవిళనఱుంబూ	నే – ని – ని – నే	గో – ధన – ధన -గో	– = = –	UIIIIU, UIIIUU, UIUIIU, UIUIUU, UIIIII, UIIIUI, UIUIII, UIUIUI
తేమాందన్నిఴల్	నే – నే – నే – ని	గో – గో – గో -ధన	– – – =	UUUII, UUUIU
పుళిమాందన్నిఴల్	ని – నే – నే – ని	ధన – గో – గో – ధన	= – – =	IIUUII, IIUUIU, IUIIII, IUUUIU
కూవిళందన్నిఴల్	నే – ని – నే – ని	గో – ధన – గో –ధన	– = – =	UIIUII, UIIUIU, UIUUII, UIUUIU
కరువిళందన్నిఴల్	ని – ని – నే – ని	ధన – ధన – గో – ధన	= = – =	IIIIUII, IIIIUIU, IIIUUII, IUIIUII, IUIUUII, IUIIUIU, IIIUUIU, IUIUUIU

ఒక స్వరపు గురులఘువుల అమరికల మొత్త సంఖ్య 4, రెండు స్వరముల గురులఘువుల అమరికల మొత్త సంఖ్య 12, మూడు స్వరముల గురులఘువుల అమరికల మొత్త సంఖ్య 36, నాలుగు స్వరముల గురులఘువుల అమరికల మొత్త సంఖ్య 108. ఈ సంఖ్యల (4, 12, 36, 108, …) అమరిక కూడ ఒక గుణశ్రేఢియే, దీని సామాన్య నిష్పత్తి 3. ఇక్కడ ఒక విశేషమును గమనించాలి. నేర్-నిరై స్వరములతో మనకు లభించే గణములు 2, 4, 8, 16, … అయితే గురు లఘువుల అమరికలు 4, 12, 36, 108. ఒక శ్రేణికి సామాన్య నిష్పత్తి 2, మఱొక దానికి 3! తమిళ ఛందస్సులోని వెణ్బా, అగవల్ వంటి ఛందములను తెలుగులో వ్రాయాలంటే ఈ గురులఘువుల అమరికలు చాల సహాయము నిస్తుంది. ఇట్టివి ఒకే చోట లేదు. రాజగోపాలరావు పుస్తకములో[2] కూడ మూడు అశైలతో ఉండే గణముల పట్టిక కూడ సగము మాత్రమే ఉన్నది. 108 గురులఘువుల అమరికతో నాలుగు స్వరముల పట్టిక అలభ్యము. ఈ పట్టికలలో 4 బ్రహ్మ గణములను ఆకుపచ్చని రంగుతో, 8 విష్ణు గణములను నీలి రంగుతో, 16 రుద్ర గణములను గులాబి రంగుతో (మొదటి రెండు చిత్రములలోవలె) చూపినాను.

కొత్త పునాది రాళ్ళు

సంస్కృత ఛందస్సులో ఏకాక్షరములు (U, I) పునాది రాళ్ళు, కన్నడ-తెలుగు దేశి ఛందస్సులో రెండు మాత్రలు (U, II) పునాది రాళ్ళు, మాత్రాఛందస్సులో మాత్రల సంఖ్యలు పునాది రాళ్ళు, తమిళ ఛందస్సులో ఏకాక్షరములు, ద్వ్యక్షరములు (U, I, II, IU) పునాది రాళ్ళు. ఒకటి రెండు మాత్రల అక్షరములను (U, I, II) ఎందుకు పునాది రాళ్ళుగా భావించ రాదనే ఆలోచన కలిగినది. అలా చేస్తే అది అన్ని ఛందస్సుల మౌలికాంశములను లీనము చేసికొన్నట్లు అవుతుంది. ఒక గురువు, ఒక లఘువు, రెండు లఘువులు – వీటికి పదేపదే వాటినే చేర్చడమువలన కొత్త గణములు సృష్టించ బడుతాయి.

3. కొత్త గణములు

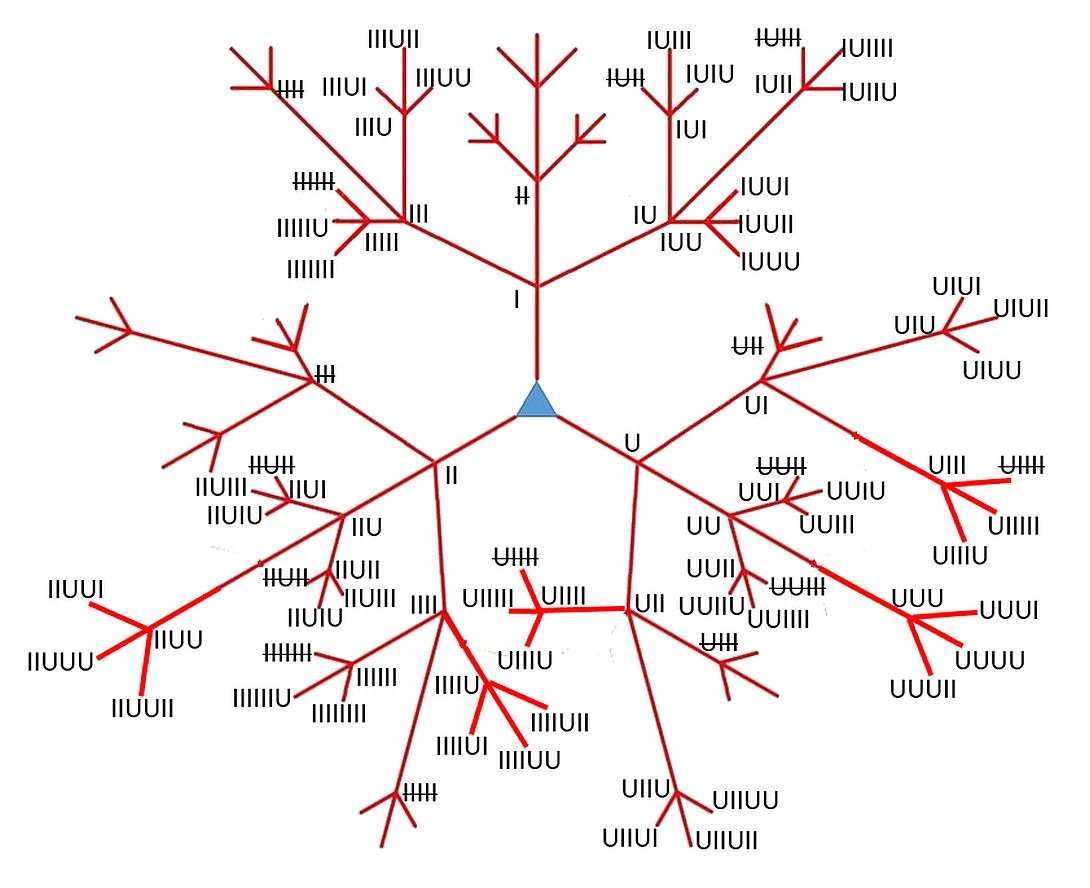
అలా చేసినప్పుడు కొన్ని గణములు మళ్ళీ వస్తాయి, ఉదా. ఒక లఘువుకు మఱొక లఘువు చేరిస్తే రెండు లఘువులు పుట్టుతాయి. కాని రెండు లఘువులు మనము ప్రారంభించిన వర్గములో ఉన్నది. కావున దానిని గ్రహించరాదు. అలా సృష్టించిన గణములకు ఆది, బుధ, గురు, తారాగణములు అని పేరునుంచినాను. వాటిని క్రింది పట్టికలో తెలుపుతున్నాను. ఈ పట్టికలో కూడ 4 బ్రహ్మ గణములను ఆకుపచ్చని రంగుతో, 8 విష్ణు గణములను నీలి రంగుతో, 16 రుద్ర గణములను గులాబి రంగుతో (మొదటి రెండు చిత్రములలోవలె) చూపినాను. మూడవ చిత్రములో ఈ గణములను వృక్షరూపములో చూడ వీలగును.

గణము	సంఖ్య	గురు లఘువుల అమరిక	విశేషములు
ఆది	3	I, U, II	1మాత్ర1, 2 మాత్రలు2
బుధ	7	IU, III, UI, UU, UII, IIU, IIII	3 మాత్రలు3, 4 మాత్రలు 4
గురు	17	IUI, IUU, IUII, IIIU, IIIII, UIU, UIII, UUI, UUU, UUII, UIIU, UIIII, IIUI, IIUU,IIUII, IIIIU, IIIIII	4 మాత్రలు1, 5 మాత్రలు8, 6 మాత్రలు8
తారా	41	IUIU, IUIII, IUUI, IUUU, IUUII, IUIIU, IUIIII, IIIUI, IIIUU, IIIUII, IIIIIU, IIIIIII, UIUI, UIUU, UIUII, UIIIU, UIIIII, UUIU, UUIII, UUUI, UUUU, UUUII, UUIIU, UUIIII, UIIUI, UIIUU, UIIUII, UIIIIU, UIIIIII, IIUIU, IIUIII, IIUUI, IIUUU, IIUUII, IIUIIU, IIUIIII, IIIIUI, IIIIUU, IIIIUII, IIIIIIU, IIIIIIII	6 మాత్రలు 5, 7 మాత్రలు20, 8 మాత్రలు16

ఈ గణముల సంఖ్యలైన 3, 7, 17, 41, … అంకెలు కూడ ఒక సంఖ్యా శ్రేణికి సరిపోతుంది. విరహాంక-హేమచంద్ర శ్రేణిని (1, 1, 2, 3, 5, 8, 13, 21, … ఇవి మాత్రఛందస్సులోని మాత్రల సంఖ్య) కొద్దిగా మార్చినప్పుడు మనకు లూకస్ సంఖ్యలు (Lucas numbers) లభిస్తాయి. లూకస్ సంఖ్యలు కొన్ని 2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, … ఈ శ్రేణికి కూడ పక్కపక్కన ఉండే సంఖ్యల నిష్పత్తి అవధిలో (limit) కరణీయ సంఖ్య φ = (√5 + 1) / 2 = 1.618033… విలువ అవుతుంది. ఈ లూకస్ సంఖ్యల వలెనే పెల్ సంఖ్యలు (Pell numbers) కూడ ఉన్నాయి. రెండు విధములైన పెల్ సంఖ్యలు ఉన్నాయి. అవి –

1, 3, 7, 17, 41, 99, 239, 577, …
1, 2, 5, 12, 29, 70, 169, 408, …

ఈ పెల్ సంఖ్యలను మనము ఈ విధముగా పుట్టించవచ్చును. P(n) = 2.P(n-1) + P(n-2). ఒక పెల్ సంఖ్య కావాలంటే ముందున్న సంఖ్యను రెట్టింపు చేసి దానికి దాని ముందున్న సంఖ్యను కలపాలి. ఉదాహరణకు మనకు పైన ఉండే మొదటి వరుసలో 99 కావాలంటే 99 = 2×41 + 17. φ = (√5 + 1) / 2 = 1.618033… వలెనే ఈ శ్రేణికి σ = (√2 + 1) = 2. 414213562… ఈ నిష్పత్తిని రజత నిష్పత్తి (silver ratio) అంటారు. ఈ సంఖ్యలకు కూడ మేరువుతో (Pascal triangle) సంబంధము ఉన్నది. పై పట్టికలోని మాత్రా గణముల సంఖ్య మేరువు నుండి మనము పొందవచ్చును. 3, 7, 17, 41, 99, ఇత్యాదులు కూడ ఒక గుణశ్రేఢియే, దీని సామాన్య నిష్పత్తి σ. స్వర్ణ నిష్పత్తి ఎలా పంచభుజిలో లభిస్తుందో, అదే విధముగా రజత నిష్పత్తి అష్టభుజిలో లభిస్తుంది. అష్టభుజిలో ఏ భుజమునకైనా సమాంతరముగా ఉండే వికర్ణపు నిడివికి భుజపు నిడివికి ఉండే నిష్పత్తి σ = (√2 + 1) = 2. 414213562… కి సరిపోతుంది.

ఇట్టి గణ సముదాయమును (ఆది, బుధ, గురు, తారా గణములను) ఉపయోగించినప్పుడు మనకు ఒక లాభము కలుగుతుంది. పింగళ ఛందస్సులోని త్రిక గణములు, కన్నడ-తెలుగు దేశి ఛందస్సులలో ఉపయోగించే బ్రహ్మ గణములు (సూర్య గణములు), విష్ణు గణములు (ఇంద్ర గణములు), రుద్ర గణములు (చంద్ర గణములు) ఇందులో ఉన్నాయి. అంతే కాక మనకు అవసరము కలిగితే ఎదురు నడకతో ఉండే గణములను కూడ వాడుటకు వీలవుతుంది, ఎందుకంటే అవి ఈ పద్ధతిలో నిషిద్ధములు కావు. ఉదాహరణకు, బుధ గణములలో IU, గురు గణములలో IUI, IUU, IUII ఉన్నాయి. ఒక గణమును కవి పద్యములో ఉపయోగిస్తారో లేదో అన్నది వారి ఇచ్ఛ. కాని కావికి కావలసిన అన్ని పనిముట్లు కవి అందుబాటులో ఉండాలి. ఆ కార్యమును ఇట్టి గణములు నెరవేరుస్తాయి.

ముగింపు

సంస్కృత, కన్నడ-తెలుగు, తమిళ, మాత్రాఛందస్సు, నేను కొత్తగా ప్రతిపాదించిన ఛందస్సు – వీటిలో గణముల సంఖ్య ఒక గుణశ్రేఢి. సామాన్య నిష్పత్తి ఒక్కొక్క దానికి ఒక్కొక్కటి. అందులో కొన్నిటికి మేరువుతో (Pascal triangle) కూడ సంబంధము ఉన్నది. తమిళములోని గణములకు సరిపోయే గురు లఘువుల వివరాలు కూడ తెలిపినాను.

గ్రంథసూచి

1. టేకుమళ్ళ రాజగోపాల రావు – ప్రాచీనాంధ్ర కవిత్వము, భారతి, క్రోధన (1925-26)
2. T Rajagopal Rao – A Comparative prosody of Dravidian languages, South Indian Literary Research Institute, 1913.