గత వెయ్యేళ్ళలో మానవుడు కనుగొన్న వాటిల్లో అతి ముఖ్యమైనది కలన గణితమేనంటే (calculus) అతిశయోక్తి కాదు. దానిని న్యూటన్, లైబ్నిట్జ్ స్వతంత్రంగా పదేళ్ళు అటూ ఇటుగా ఒకే కాలంలో కనుక్కున్నారు. ఎవరు ముందు కనుక్కున్నారు అన్నదానిమీద చాలా స్పర్ధలొచ్చాయి. తెలుగు వాళ్ళలో పెద్దగా చదువుకోని వాళ్ళలో కూడా న్యూటన్ పేరు వినని వాళ్ళుండరు. కాని బాగా చదువుకున్న వాళ్ళలో కూడా ఎంతో మందికి లైబ్నిట్జ్ ఎవరో తెలియదు. నడిచే విజ్ఞాన సర్వస్వంగా, అపర అరిస్టాటిల్గా పేరు తెచ్చుకున్న లైబ్నిట్జ్ జీవితాన్నీ, బహుముఖ ప్రతిభనీ, కంప్యూటర్ సైన్సుకి మూలాధారమైన అతని విప్లవాత్మక ఆలోచనలనీ ఈ వ్యాసం ద్వారా రేఖామాత్రంగానయినా పరిచయం చెయ్యాలని నా ఉద్దేశం.
జీవిత సంగ్రహం
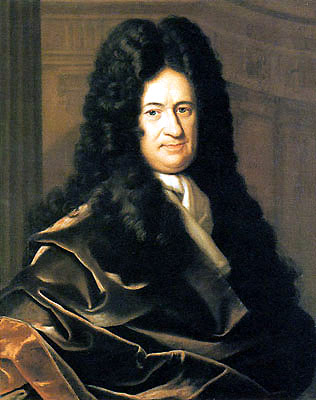
గాట్ఫ్రీడ్ విల్హెం లైబ్నిట్జ్ (1646-1716)
గాట్ఫ్రీడ్ విల్హెం లైబ్నిట్జ్ 1646లో జర్మనీలోని ప్రొటెస్టెంట్ నగరం, లీప్జిగ్లో పుట్టాడు. తండ్రి యూనివర్సిటీ ప్రొఫెసరు. తల్లిగూడా బాగా చదువుకున్నది. పుట్టిన మూడే రోజే బాప్టైజ్ చేసే సమయాన, పూజారి చల్లిన పవిత్ర జలాన్ని తలెత్తి స్వీకరించడం చూసి, తండ్రి కొడుకు గొప్పవాడవుతాడని కలలుగన్నాడు. చిన్నప్పుడే చరిత్ర పుస్తకాలు చదివించాడు. అయితే కొడుకు ఆరేళ్ళలోపు వయసులో ఉన్నప్పుడే ఆయన చనిపోయాడు. లైబ్నిట్జ్ చిన్నతనంలో ఆటలన్నా పాటలన్నా అంత ఇష్టం చూపకుండా చదువులో నిమగ్నమయుండే వాడు. బళ్ళో పైక్లాసు వాళ్ళ పుస్తకాలు చదవడం చూసి, మాష్టారు వాళ్ళమ్మతో ఫిర్యాదు చేసి వయసుకి మించిన పుస్తకాలని అందుబాటులో ఉంచొద్దని హెచ్చరించాడు!
లైబ్నిట్జ్ బంధువొకాయన విషయం తెలుసుకొని, పిల్లవాడితో మాట్లాడి, అసామాన్య ప్రతిభావంతుడని గుర్తించి, వాళ్ళమ్మతోచెప్పి వాళ్ళ నాన్న లైబ్రరీ గదికి తాళం తీసి అబ్బాయి వెళ్ళేటట్లు చూశాడు. అప్పుడు లైబ్నిట్జ్ వయసు ఎనిమిదేళ్ళు! లాటిన్, గ్రీక్ పుస్తకాలు విపరీతంగా చదివాడు. పన్నేండెళ్ళొచ్చేటప్పటికి లాటిన్ క్షుణ్ణంగా వచ్చేసింది. కవిత్వం రాయగలిగేటంత! అంతటి పాండిత్యం గ్రీకులో గూడా సాధించడానికి తయారయ్యాడు.
అప్పట్లో జర్మనీలో గణితశాస్త్రం అంతగా అభివృద్ధి చెందలేదు కాని, బళ్ళో అరిస్టాటిల్ తర్కం నేర్పేవాళ్ళు. అది లైబ్నిట్జ్లోని జీనియస్ని మేల్కొల్పింది. అరిస్టాటిల్ రెండు వేల సంవత్సరాల క్రితం విజ్ఞాన సర్వస్వాన్ని క్రోడికరించ ప్రయత్నించాడు. లైబ్నిట్జ్కి ఓ మనోహరమైన ఊహ కలిగింది: మనం మాట్లాడే భాషలో అక్షరాలు, వాటితో కూడి మాటలు, మాటలతో కూడి వాక్యాలు ఉన్నాయి. అలాగే భావాలని (concepts) అక్షరాలుగా, వాటిని వ్యాకరణ సూత్రాలవంటి వివేచన సూత్రాలనాధారంగా ఓ విజ్ఞాన భాషని తయారుచేస్తే, మనం మాట్లాడినంత సులభంగా, అన్ని విషయాలను గురించీ విచారణ చెయ్యొచ్చని ఊహించాడు. ఈ భావన జీవితాంతమూ లైబ్నిట్జ్ ఆలోచనలలో ప్రకాశిస్తూనే ఉంది.
పదిహేడేళ్ళకే బ్యాచలర్ డిగ్రీ సంపాదించాడు. అపుడే తల్లినికూడా కోల్పోయాడు. ఇరవై ఏళ్ళకే న్యాయ శాస్త్రంలో డాక్టరేట్ కోసం థీసిస్ రాశాడు. లీప్జిగ్ యూనివర్సిటీ ప్రొఫెసర్లు మరీ చిన్నవాడు అనే సాకుతో, తమకంటె ఎక్కువ తెలుసుననే ఈర్ష్యతో డిగ్రీ ఇవ్వడానికి ఒప్పుకోలేదు. వాళ్ళ మీద అసహ్యం వేసి, సొంత ఊరుని వదిలి, న్యూరెంబెర్గ్ వెళ్ళాడు. వెళ్ళే త్రోవలోనే న్యాయశాస్త్రం బోధించడానికి కావలసిన కొత్తమార్గాలపై ఓ వ్యాసం రాశాడు. దానికి ఆల్ట్డార్ఫ్ యూనివర్సిటీ వాళ్ళు ముగ్ధులై డాక్టరేట్ ఇవ్వడమే కాక, ప్రొఫెసర్ ఉద్యోగం ఇచ్చి, చేరమని ప్రాధేయపడ్డారు. యూనివర్సిటీ ప్రొఫెసర్ జీవితం సంకుచితమైనదని భావించి ఆ ఉద్యోగాన్ని నిరాకరించాడు.
మరి జీవనోపాధికి మార్గమేమిటి? డాక్టరేట్ కోసం రాసిన వ్యాసం బోయింబెర్గ్ అని ఓ సంపన్నుడైన వ్యవహారవేత్త కంటబడింది. దానిని మెయింజ్ ఆర్చిబిషప్కి అంకితం చెయ్యమని చెప్పాడు బోయింబెర్గ్. అది చూసి లైబ్నిట్జ్కి ఓ న్యాయపదవి ఇచ్చారు. దౌత్యవ్యవహారాల మీద దేశదేశాలు పర్యటించాడు. యుద్ధ వ్యూహాలు కూడా పన్నాడు.
అప్పట్లో జర్మనీ కొన్ని వందల రాజ్యాలుగా విడిపోయి ఉంది. ఫ్రాన్సు యూరప్లో “అగ్రరాజ్యం” స్థాయిలో ఉంది. ఆ దేశపు రాజయిన 14వ లూయీ తన అధీనంలో లేని రాజ్యాలపై దండయాత్ర చేసి వశం చేసుకుంటున్నాడు. మెయింజ్ రోమన్ సామ్రాజ్యం క్రింద రావడంతో ఫ్రాన్స్ చేతిలో ముప్పు దాపురింఛి ఉందని గ్రహించిన లైబ్నిట్జ్ ఓ పథకం వేశాడు. యూరపియన్లు యూరప్లో వాళ్ళమీద దండయాత్ర చేస్తే ఒరిగేదేమిటి, ఈజిప్టు మీద యుద్ధం చేస్తే ఆర్థికంగా లాభం ఉందని ఓ ప్రతిపాదన చేశాడు. దానిని 14వ లూయూకి సమర్పించడానికని 1672లో పారిస్ వెళ్ళాడు.
పారిస్లో రాజదర్శనం దొరకలేదు. పారిస్ ఆకాలంలో యూరప్లోకెల్లా పెద్ద వికాస కేంద్రం; విజ్ఞానవేత్తలెందరికో కూడలి. వాళ్ళ సాంగత్యం కోసం లైబ్నిట్జ్ అక్కడే ఉండాలని అభిలాషపడ్డాడు. పారిస్ వెళ్ళిందాకా అతనికి ఆధునిక గణితశాస్త్రంలో సరయిన శిక్షణా అవగాహనా లేవు. అక్కడ హాలండ్ దేశస్థుడైన క్రిస్టొఫెర్ హైగెన్స్ని (Christopher Huygens) కలుసుకున్నాడు. ఆయన లెక్కల్లో ఓ చిన్న పరీక్ష పెట్టాడు. దానికి లైబ్నిట్జ్ సరిగ్గా సమాధానం చెప్పాడు. స్వతహాగా తెలివయిన వాడని గ్రహించి, మెచ్చుకొని, లెక్కల్లో పాఠాలు చెప్పాడు. చదవమని చాలా పుస్తకాలిచ్చి ప్రోత్సహించాడు. అంటే లైబ్నిట్జ్ ఇరవై ఆరేళ్ళ వయసొచ్చిందాకా గణితంలో క్రమమైన శిక్షణ పొందలేదన్నమాట!
అక్కడ నుండి లైబ్నిట్జ్ వ్యాపార వ్యవహారాల మీద లండన్ వెళ్ళాల్సిన పనిబడింది. లండన్లో రాయల్ సొసైటీ సభ్యులని కలిశాడు. విజ్ఞానశాస్త్రాల్లో అభిరుచికలవాళ్ళు తమతమ ఆలోచనలనీ పరిశోధన వివరాలనీ పంచుకోడానికి పెట్టుకున్న సంస్థ అది. వాళ్ళకి తన కాల్కులేటింగ్ యంత్రాన్ని చూపాడు. దానిని చూసి వాళ్ళు అతన్ని మొదటి విదేశ ఫెలో గా తీసుకున్నారు. అక్కడి వాళ్ళతో పోలిస్తే తనకి గణితంలో తగినంత పరిజ్ఞానం లేదని గ్రహించాడు. పారిస్ తిరిగొచ్చి అధ్యయనం పెంచాడు.
జీవితం అంతా ఇంతే. ప్రభువుల పని మీద ఏ దేశం వెళ్ళినా, ఆ పనితో పాటు అక్కడ జరిగే అనేక వ్యవహారాల్లో తలదూర్చడం, పండితులతో సంబంధాలు పెంచుకోవడం, విజ్ఞానానికి సంబంధించి అన్ని శాఖల్లోకీ ప్రవేశించి మౌలికమైన ఆలోచనలు చెయ్యడం! బండిలో గానీ నావలో గానీ, తన దేశంలో ఉన్నా పరాయి దేశంలో ఉన్నా, ఏ పరిస్థితుల్లోనూ ఎడతెరిపిలేని ఆలోచనలే. చదవడానికీ రాయడానికీ ఆటంకం లేదు. “నేను ప్రచురించిన వాటిని మాత్రమే చూసి నన్ను అంచనా వేసే వాళ్ళకి నా శక్తిసామర్థ్యాలు తెలియవు,” అన్న మాటల్లో అతిశయోక్తి లేదు. కొన్ని వందలమందితో జీవితాంతం ఉత్తర ప్రత్యుత్తరాలు జరిపాడు. పదిహేను వేలకి పైగా జాబులురాశాడు. తాను స్పృశించని సమకాలిక అంశం లేదు.
పారిస్ నచ్చింది. కాని పోషిస్తున్న బోయింబెర్గ్ చనిపోయాడు. జీవనభృతికి ఆటంకం కలిగింది. పారిస్లో ఏదన్నా ఉద్యోగం ఇస్తారని చూశాడు. ఏమీ దొరకలేదు. సైన్సు అకాడెమీలో అప్పటికే విదేశీయులు ఎక్కువయ్యారని తీసుకోలేదు. జర్మనీలోని ఓ రాజు (Duke of Hanover) దివాణంలో ఉద్యోగం దొరికింది. అయినా పారిస్ వదలి వెళ్ళ బుద్ధి కాలేదు. ఆ సాకూ ఈ సాకూ చెప్పి పొడిగించాడు. సాగినంతకాలం పారిస్లోనే గడిపాడు. ఇక ప్రభువుకి చిరాకు కలగడంతో, హానోవర్ వచ్చి ఉద్యోగంలో చేరతాననీ, మానవశ్రేయస్సుకోసం విజ్ఞానశాస్త్రాల్లో కృషి చెయ్యడానికి అనుమతి ఇవ్వమనీ కోరుకున్నాడు. 1676లో పారిస్ వదిలాడు. మళ్ళీ పారిస్ సందర్శించలేదు. చనిపోయిందాకా హానోవర్ రాజవంశం సేవలో గడిపాడు.
లైబ్రరీ నిర్వహణ, పాలనా యంత్రం, వ్యవసాయం, వైద్యం, ఇలా అన్నిటినీ అభివృద్ధిచెయ్యడానికి కృషిచేశాడు. కొత్తకొత్త మార్గాలని కనిపెట్టాడు. అయితే చేరిన నాలుగేళ్ళకే ప్రభువు చనిపోయాడు. కొత్త ప్రభువు, Ernst August కి మేధో విషయాలపైన అంత ఆసక్తి లేదు. లైబ్నిట్జ్ జీవనోపాధికి మళ్ళీ ఆటంకం కలిగేలా ఉంది. అందుకని, ఆ రాజవంశం చరిత్ర రాస్తానన్నాడు. అది ప్రభువుకి నచ్చింది. దానికి కొంత జీతం, ఓ సెక్రటరీని ఇచ్చారు.
లైబ్నిట్జ్ పిసినిగొట్టు అని చెప్తూ, బర్ట్రాండ్ రస్సెల్, “అంతఃపురం లోని ఆడవాళ్ళకి పెళ్ళి కానుకగా, నగా నట్రా ఏమీ ఇవ్వకుండా, ఓ చిన్న కవిత – అదీ, పెళ్ళయింది గదా అని పని చెయ్యడం మానవద్దని హితోపదేశం చేస్తూ – రాసి ఇచ్చేవాడు,” అన్నాడు! ఆ పెళ్ళికానుకల వల్ల వచ్చిన ఖ్యాతి మూలంగానేమో, చాలా కాలమయినా పెళ్ళి కాలేదు. యాభై ఏళ్ళ వయసొచ్చింతర్వాత ఒకావిడంటే ఇష్టపడి, పెళ్ళి చేసుకోమని అడిగాడు. ఆవిడ “ఆలోచిస్తాను,” అంది. హతాశుడైన మేధావి ఇక పెళ్ళి ప్రసక్తి తేలేదు.
అలాగని లైబ్నిట్జ్కి ఆడవాళ్ళంటే చిన్నచూపు అనుకోడానికి ఆస్కారం లేదు. రాణి Duchess Sophie తోటీ యువరాణి Sophie Charlotte తోటీ తాత్విక విషయాల గురించి ఎక్కువగా సంభాషించేవాడు. తన జీవితకాలంలో ప్రచురించిన ఒకే ఒక పుస్తకం, థియోడసీ (Theodicy), ఆ సంభాషణల సారాంశమే అన్నాడు! బెర్లిన్ సైన్సు అకాడెమీని స్థాపించడానికి రాణి సాయం కోరాడు. ఆడవాళ్ళని సభ్యులుగా నియమించాలన్నాడు. అప్పట్లో అది చెప్పుకోదగ్గ విషయం.
వంశ చరిత్ర రాయడానికి చెయ్యాల్సిన పరిశోధన సాకుగా దేశదేశాలు తిరిగాడు. ఆ పర్యటనలని తన మేధోగత విషయాలకై వాడుకున్నాడు. కాని ఆ వంశ చరిత్ర రాయడమన్నది ఒక గుదిబండగానే తయారయ్యింది. రాజు లండన్ వెళ్ళినా లైబ్నిట్జ్ని హానోవర్ లోనే ఉండి తమ వంశచరిత్ర పూర్తి చెయ్యాలని ఆదేశించాడు. రాణి మరణం తర్వాత ఆదరణా తగ్గింది. చివరకి చనిపోయినపుడు సెక్రటరీ కి మించి అంత్యక్రియలకి హాజరైన వాళ్ళు లేరు! తను స్థాపించిన అకాడెమీల నుండి ఎవరూ రాలేదు. చనిపోయిన యాభై ఏళ్ళ దాకా సమాధిని ఎవరూ అలంకరించిన పాపాన పోలేదు. “దేశానికే ఆభరణం లాంటివాడు, ఒక అనామకుడిగా మరణించాడు.”
లైబ్నిట్జ్ చక్రం
“For it is unworthy of excellent men to lose hours like slaves in the labour of calculation which would safely be relegated to anyone else if machines were used” (G.W. Von Leibniz)

లైబ్నిట్జ్ చక్రం
ఆధునిక యుగంలో ఆడవాళ్ళకీ మగవాళ్ళకీ కూడా, వయసుతోపాటు బరువు పెరుగుతోందన్న ఆందోళన ఎక్కువ. బరువుని అదుపులో పెట్టడానికి అనేక రకాల వ్యాయామాలు, వాటికి సంబంధించిన పరికరాలు ఉన్నాయి. వాటిల్లో ఒకటి అడుగులని లెక్కపెట్టేది “పెడోమీటర్” (Pedometer) . ప్రొద్దున్నే నడుందగ్గర తగిలించుకొని దాని విషయం మరచిపోవచ్చు. రాత్రి పడుకోబోయే ముందు చూసుకుంటే ఆరోజున ఎన్ని అడుగులు వేశామో చెప్తుంది!
అలాంటిదాన్నొకదానిని 1672 ప్రాంతంలో దౌత్యవ్యవహారం మీద పారిస్ వెళ్ళినప్పుడు లైబ్నిట్జ్ చూశాడు. వెంటనే ఓ అమోఘమైన అయిడియా వచ్చింది: అడుగు వేసినప్పుడల్లా ఆటోమాటిక్గా ఒకటి కూడుతోంది గదా; అదే సూత్రం మీద, కూడికలూ తీసివేతలూ, హెచ్చవేతలూ భాగహారాలూ చేసే యంత్రాన్ని ఎందుకు చెయ్యలేము?
లైబ్నిట్జ్ పారిస్ వెళ్ళింది రాజకీయపు పనులమీదనే అయినా, వీలుదొరికినపుడల్లా లైబ్రరీలకెళ్ళి అనేక విషయాలమీద చదివేవాడు. ఒకరోజు పాస్కల్ (Pascal 1623-1662) అని గణిత శాస్త్రజ్ఞుడయిన తత్వవేత్త రాసిన ఒక పుస్తకం చదువుతుంటే దాంట్లో కాల్కులేటింగ్ యంత్రం పేరు కనిపించింది. వెంటనే పారిస్ లోని మిత్రులని అడిగి అలాంటిదొకటి పాస్కల్ చేశాడని తెలుసుకుని, దానికి సంబంధించిన వివరాలన్నీ ఆరా తీశాడు.
పాస్కల్ బాల్య మేధావి. వాళ్ళ నాన్న పన్నులు వసూలు చేసే అధికారి. ఆ లెక్కలు వెయ్యడానికి ఆయన పడే అవస్థ చూసి, పాస్కల్ పన్నేండేళ్ళ వయసులోనే కూడికలూ తీసివేతలూ సులభంగా త్వరగా చేసే యంత్రాన్ని తయారు చేశాడు! జీవితం మధ్యలో ఆధ్యాత్మిక చింతన పెరిగి విజ్ఞానశాస్త్రాలకి దూరమయ్యాడు.
(ఆధునిక యుగంలో నిక్లాస్ వర్త్ (Niklaus Wirth) అనే స్విస్ కంప్యూటర్ శాస్త్రవేత్త ఓ చిన్న ప్రోగ్రామింగ్ లాంగ్వేజ్ ని రూపొందించి దానికి పాస్కల్ (Pascal) అని పేరు పెట్టాడు. ఈ మధ్యదాకా యూనివర్సిటీలలో ప్రోగ్రామింగ్ నేర్పడానికి ఈ భాషనే వాడేవాళ్ళు. ప్రోగ్రామింగ్ భాషలని రూపొందించిన కృషికి గుర్తింపుగా వర్త్ కి 1984 టూరింగ్ అవార్డు ఇచ్చారు.)
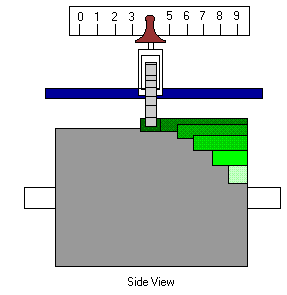
లైబ్నిట్జ్ చక్రం (ఒక పక్క నుండి చూస్తే)
పాస్కల్ యంత్రం కన్నా మించి కూడికలూ తీసివేతలే కాక, హెచ్చవేతలూ భాగహారాలూ కూడా చేసే యంత్రాన్ని లైబ్నిట్జ్ తయారుచేశాడు. దీంట్లో ప్రత్యేకత ఓ కొత్త రకమైన డ్రమ్ము. దాని ఉపరితలం మీద వేర్వేరు పొడుగున్న పళ్ళు – ఒకటి నుండి తొమ్మిది దాకా – మెట్లు లాగా చెక్కి ఉంటాయి (stepped drum). దానిని లైబ్నిట్జ్ చక్రం (Leibniz Wheel) అంటారు. ఈ డ్రమ్ము పైన మామూలు పళ్ళ చక్రం ఉంటుంది. దానిని డ్రమ్ము పైన వేరు వేరు చోట్ల కావలసిన అంకెకి సరిపడేటట్లుగా జరిపి పెట్టొచ్చు. అప్పుడు డ్రమ్ము ని ఒక రౌండు త్రిప్పితే పళ్ళ చక్రం అంకెకి సమానమయిన అంచెని తాకి అందుకు సమానమయినంత కదులుతుంది. రెండో ప్రపంచ యుద్ధం కాలం దాకా కూడా ఈ నమూనా మీద ఆధారపడి ఉన్న కాలిక్యులేటర్లనే వాడేవాళ్ళు! దీని గురించి ఇంకా వివరాలు ఇక్కడ చదవొచ్చు.

లైబ్నిట్జ్ చక్రం (ఒక చివరి నుండి చూస్తే)
ఈ యంత్రాన్ని ఆపరేట్ చెయ్యడానికి కావలసింది మీటలు నొక్కడం, ఇరుసుతో చక్రాన్ని తిప్పడం! పెద్దగా శిక్షణ లేకుండా ఎవరైనా చెయ్యొచ్చు. దీనిని లండన్లో రాయల్ సొసైటీ ముందు ప్రదర్శించాడు. ఈ కాలంలో సాఫ్ట్వేర్ డెమో చేసినట్లన్నమాట. ఇప్పటిలాగే అప్పుడు కూడా ప్రకటించిన వాటిలో సగమే పనిచేశాయి! ఇప్పటి సాఫ్ట్వేర్ ఇంజనీర్ల లాగానే లైబ్నిట్జ్ కూడా, “ఇది బీటా రిలీజు. రెండు మూడు నెలల్లో లోపాలు తొలగిస్తాను,” అని మాట ఇచ్చాడు.
ఈ యంత్రం చెయ్యగలిగింది సర్వసాధారణమైన లెక్కలే. లైబ్నిట్జ్ కన్నా ముందరే కొందరు అలాంటి యంత్రాలు చేశారు. కాని లైబ్నిట్జ్ గొప్పతనం గణన (calculation) స్వభావాన్ని కనిపెట్టడటం – అది యాంత్రికం అని తేల్చేయడం! సృజనీయకమైన పనిచెయ్యగల వాళ్ళు యాంత్రికమైన పనులు చెయ్యడం అవమానకరం అన్నాడు.
సులువైన ద్వియాంశ గణితం (Binary Arithmetic)
సర్వసాధారణమయిపోయిన వాటి ఘనత వెంటనే గ్రహించం. అనాదిగా మానవులకి లెక్కించవలసిన అవరం ఉంది – వేటలో దొరికిన చేపలెన్ని, పశువులెన్ని ఉన్నాయి, పిల్లలెంతమంది, బానిసలెంతమంది, సైనికులెంతమంది. చేతి వేళ్ళని దాటిపోవాల్సిన అవరం వచ్చినప్పుడు వేరే పద్ధతుల్ని కనుక్కున్నారు. సంఖ్యలకి సంకేతాలు పెట్టుకున్నారు. అయితే ఈ సంకేతాలు బండ గుర్తులగా పనికొచ్చాయా, లేక సులభంగా లెక్కలు చెయ్యడానికి సోపానాలయ్యాయా అని అడిగితే మానవ చరిత్రలో చాలా కాలం వరకు కేవలం బండ గుర్తులగానే పనికొచ్చాయని చెప్పక తప్పదు!
ప్లేటో, ఆర్కిమెడిస్ లాంటి మహామేధావులున్న గ్రీకులనే తీసుకోండి. రెండు వేల సంవత్సరాలకి పూర్వమే రేఖాగణిత (geometry) శాస్త్రాన్ని వాళ్ళు అద్భుతంగా అభివృద్ధి చేశారు. అంతకన్నా మౌలికమైన అంకగణితం (arithmetic) లో మాత్రం వాళ్ళు శైశవస్థాయిని గూడా దాటలేదు. కారణం వాళ్ళు సరయిన సంకేతాల ప్రాధాన్యత గుర్తించలేకపోవడమే!
ఇటీవలదాకా యూరప్లో కూడికలూ తీసివేతలూ చెయ్యడం సామాన్యమానవుడికి సాధ్యం కాలేదు. అక్కడ మధ్యయుగాలలో కూడా రోమన్ అంకెలు వాడేవాళ్ళు. ఆ పద్ధతిలో చిన్న చిన్న సంఖ్యలు రాయడం కూడా పెద్ద తలనొప్పే. ఇప్పుడు రోమన్ అంకెలు గడియారాల్లో అలంకారానికీ, ఆటల్లో ఆర్భాటానికీ ఆచారానికీ తప్ప విజ్ఞానశాస్త్రాల్లో కనబడవు.
ప్రస్తుతం అన్ని దేశాల్లోనూ చిన్న పిల్లలు కూడా కూడికలూ తీసివేతలూ చెయ్యగలుగుతున్నారంటే దానికి మూలకారణం దశాంశపద్ధతే (decimal system). దీనిని కనుక్కున్నది మన భారతీయులే. నిన్నా మొన్నా కాదు. రెండు వేల సంవత్సరాల క్రితం! మన నుంచి అరబ్బులు నేర్చుకుంటే వాళ్ళని యూరోపియన్లు మతయుద్ధాలలో (Crusades) వశం చేసుకున్నతర్వాత దశాంశపద్ధతి “చాప కింద నీరు”లా యూరప్ చేరింది మధ్య యుగాల్లోనే! (దశాంశ పద్ధతిని మనకన్నా ముందరే చైనీయులు కనుక్కున్నారని కొందరు పండితులు వాదిస్తున్నారు. అది ఒక వేళ నిజమే అయినా, ప్రపంచమంతా వాడుకలో ఉన్న ప్రస్తుత పద్ధతి మన దేశం నుంచే వ్యాప్తి అయిందని ఎక్కువ మంది ఒప్పుకుంటారు.)
దశాంశ పద్ధతికున్న విశిష్ట గుణాలు మూడు: 1) స్థానాన్నిబట్టి విలువ కట్టడం – దీనితో ఎంత పెద్ద సంఖ్యనయినా క్రమంగా క్లుప్తంగా రాయొచ్చు. 2) అందుకు కావలసిన పది అంకెలకి నిర్దిష్టమైన సంకేతాలివ్వడం. 3) శూన్యానికున్న ప్రాముఖ్యతని గుర్తించి దానికి ప్రత్యేకమైన సంకేతాన్ని (0) ఇవ్వడం.
చిన్నప్పుడు కప్పు ఎగిరిపొయ్యేలా ఎక్కాలు చదవడం, తప్పుచేస్తే తొడపాశాల పాలవడం గుర్తొస్తే ఈ దశాంశపద్ధతిని నేర్చుకోవడానికి కూడా కొన్నేళ్ళు పడుతుందని అర్థమవుతుంది. ఎందుకంటే, 9+7 ఎంతంటే మనం వేళ్ళు లెక్కపెట్టాలి. 9×7 ఎంతంటే బట్టీ వేసినదాన్ని గుర్తు తెచ్చుకోవాలి. వేళ్ళు మూయడం తెరవడంలో గానీ, ఎక్కాల పట్టికని గుర్తు తెచ్చుకోవడంలో గానీ, ఏ కొంచెం తప్పు చేసినా లెక్కంతా తారుమారవుతుంది.
ఇంతకన్నా సులభ మార్గముందా? పది అంకెలు వాడకుండా క్లుప్తమయిన పద్ధతి ఉందా? అని లైబ్నిట్జ్ ఆలోచించి ద్వియాంశ పద్ధతిని (రెండంకెల గణితాన్ని) కనిపెట్టాడు. దీనిని కూడా మన దేశస్థుడయిన పింగళుడు కవిత్వంలో గురువుల లఘువుల ప్రాధాన్యతని వివరిస్తూ, క్రీస్తుకి పూర్వమే కనుక్కున్నాడని చెప్తారు కాని, దానిని పూర్తిగా వివరించిన వాళ్ళలో మొదటివాడు లైబ్నిట్జ్ అని గుర్తించాలి.
ద్వియాంశ పద్ధతిలో ఉన్నది రెండే రెండు అంకెలు (0, 1) కావడాన దాంట్లో లెక్కలు చెయ్యడం చాలా సులభం. వాటితో ఎంత పెద్ద సంఖ్యనయినా రాయొచ్చు. క్రింది స్థానాలనుండి పై స్థానాలకి వెళ్ళేకొలదీ దశాంశ పద్ధతిలో ఒకటి, పది, వంద, వెయ్యి, … ఇలా స్థాన విలువ పదింతలయినట్లే ద్వియాంశ పద్ధతిలో ఒకటి, రెండు, నాలుగు, ఎనిమిది, పదహారు, ముప్ఫై రెండు, అరవై నాలుగు, … ఇలా స్థాన విలువ రెండింతలవుతుంది. అంతే తేడా. ఉదాహరణకి మొదటి పది సంఖ్యలనీ (0 నుండి 9 దాకా) ద్వియాంశ పద్ధతిలో ఇలా రాస్తారు: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001.
కేవలం రెండు అంకెలతో సంఖ్యలని గుర్తించగలిగినంత మాత్రాన పెద్ద ప్రయోజనం లేదు. సంఖ్యలతో చేసే పనులు సులభంగా చెయ్యవచ్చా లేదా అన్నదే ముఖ్యం. అందుకు ఏమాత్రమూ సందేహం లేదు. కూడికలూ తీసివేతలూ చెయ్యడానికి కాళ్ళూ చేతులూ వాడాల్సిన అవసరం లేదు: 0+0=0; 1+0=1; 0+1=1; 1+1=10 (అంటే రెండు). హెచ్చవేతలకి ఎక్కాల పట్టికని కంఠస్థం చెయ్యాల్సిన అగత్యం లేదు: సున్నాని సున్నాతో పెంచినా ఒకటితో పెంచినా సున్నాయే; ఒకటిని ఒకటితో పెంచితే ఒకటే! 0x0=0; 0x1=0;1×0=0;1×1=1. ఇదెంతో సహజంగానూ గుర్తుంచుకోడానికి ఎంతో సులభంగానూ ఉందని అందరూ ఒప్పుకుంటారు.
తను కనుక్కున్న పద్ధతిని చూసుకొని లైబ్నిట్జ్ చాలా మురిసిపోయాడు. ఒకటి దేవుడికీ, సున్నా శూన్యానికీ చిహ్నాలనీ, దేవుడు శూన్యాన్నించి ప్రపంచాన్ని సృష్టించాడన్న తన తత్వానికి కూడా దీనిని అన్వయించుకున్నాడు!
ద్వియాంశ పద్ధతితో ఒకటే ఇబ్బంది. సంఖ్యలు చాలా పొడుగయి రోజువారీ జీవితంలో వాడటానికి అసౌకర్యంగా ఉంటాయి. ఒకరి వయసు 50 సంవత్సరాలు అని రాయడానికి బదులు 110010 అని (32×1 + 16×1 + 8×0+ 4×0 + 2×1 + 1×0 = 50) రాయాలి. అందువలన దశాంశ పద్ధతినే వాడుకలో ఉంచాలని లైబ్నిట్జ్ భావించాడు.
అయితే అతి తక్కువ అంకెలతో గణితం సాధ్యం కావడాన, దీనితో లెక్కల్ని యాంత్రికంగా సులభంగా తప్పులు లేకుండా చెయ్యొచ్చనీ, అందుకు చక్రాలూ, గేర్లూ లేకుండా, మూసుకునే తెరుచుకునే రంధ్రాలున్న జల్లెడలాంటి పరికరంతో యంత్రాన్ని ఎలా తయారుచెయ్యవచ్చో రూపకల్పన గూడా చేశాడు!
ఇప్పుడు ఓ క్షణం లైబ్నిట్జ్ కాలం దాటి రెండు మూడు వందల ఏళ్ళు ముందున్న ఎలెక్ట్రానిక్ యుగంలోకొద్దాం. 1945లో జాన్ ఫాన్ నోమన్ (John von Neumann) అని ఓ గొప్ప గణిత శాస్త్రజ్ఞుడు కంప్యూటర్ల నిర్మాణం గురించి ఓ రిపోర్టు రాశాడు. ఈ మేధావిని గురించి ముందు ముందు తెలుసుకుందాం. ఇప్పటికీ గూడా అన్నిరకాల కంప్యూటర్లనీ ఆయన నిర్దేశించిన నిర్మాణ పద్ధతిలోనే చేస్తున్నారు! ఆ రిపోర్టులో ద్వియాంశ పద్ధతిని ఎందుకు వాడాలో వివరించాడు: 1) కంప్యూటర్లలో ఉండే ఎలెక్ట్రానిక్ సర్క్యూట్ గేట్లు ఒక స్థితి నుండి మరొక స్థితికి అతి త్వరగా మారుతుంటాయి. గేటు ఎప్పుడూ తెరచిగానీ (off) మూసిగానీ (on) ఉంటుంది. గేట్లు ఈ రెండే స్థితులలో ఉండటాన వాటితో రెండంకెల గణితం చాలా సులభంగానూ వేగంగానూ చెయ్యొచ్చు. 2) కంప్యూటర్ కంట్రోల్ అంకగణితం మీద కన్నా ఎక్కువగా తర్కం మీద ఆధారపడి ఉంటుంది – తర్కంలో కూడా రెండే విలువలు (True or False, నిజమా కాదా?) ఉండటం వల్ల రెండంకెల పద్ధతి అనుకూలంగా ఉంటుంది. అందువలన ఇప్పటి కంప్యూటర్లలో ద్వియాంశ పద్ధతినే వాడుతున్నాం.
దీంట్లో మనం ముఖ్యంగా గుర్తించాల్సిన లైబ్నిట్జ్ ప్రతిభేమిటంటే క్లిష్టమైన భావాలని సరళమైన భాషలో క్లుప్తమైన గుర్తులతో వాడటం. చిన్న చిన్న మౌలికమైన కార్యాల (operations) ద్వారా పెద్ద పెద్ద సమస్యలని సాధించగలగడం. ఇది అతను జీవితాంతం చేస్తూనే ఉన్నాడు – తత్వశాస్త్రం, న్యాయశాస్త్రం, చరిత్ర, గణితం, భౌతిక శాస్త్రం – ఏది చేపట్టినా దానికి కొంత క్రమమైన భావన తీసుకురావడానికి నిర్విరామంగా కృషిచేశాడు. ద్వియాంశ గణితం లైబ్నిట్జ్ జీనియస్కి మరో మచ్చుతునక.
వికాసయుగాల గణితవజ్రం కలనగణితం (Calculus)
నేను మొదటిసారిగా 2004లో పారిస్ వెళ్ళాను. అదో అద్భుత నగరం. వీధుల్లో తిరుగుతూ వికాసకాలపు విజ్ఞానవేత్తలని గుర్తుచేసుకోవడం గొప్ప అనుభూతి. అక్కడున్న ఐఫెల్ టవర్ గురించి అందరూ వినే ఉంటారు. ఆ కట్టడం మీద ఐఫెల్ 72 మంది పేర్లు – ఫ్రెంచి ఇంజనీర్లవీ శాస్త్రవేత్తలవీ – చెక్కించాడు. వీళ్ళంతా పదునెనిమిదవ శతాబ్దపు వాళ్ళు. లాప్లాస్, లాగ్రాంజ్ లాంటి వాళ్ళ పేర్లు కాలేజీ పుస్తకాల్లో చదువుకున్నవే. ఆ పేర్లు చదువుతుంటే నాకో విషయం తలపుకొచ్చింది. చిన్న దేశమయిన ఫ్రాన్సు లోనే అంతమంది ప్రముఖ శాస్త్రవేత్తలుంటే ఎంతో పెద్దదయిన మన దేశంలో వేళ్ళమీద లెక్కబెట్టగలిగేటంతమంది కూడా ఎందుకు లేకపోయారు? అని.
విజ్ఞానశాస్త్రచరిత్రకారులకి ఇప్పటికీ చిక్కువీడని సమస్య ఒకటుంది. క్రీ.శ. 1600 దాకా యూరోపియన్ దేశాలు ఇండియా, చైనా, అరబ్బు దేశాలకన్నా ముందేమీ లేవు. నిజానికి గణితంలో యూరప్ మిగిలిన దేశాల కంటె వెనుకబడి ఉంది. ఆ తర్వాత యూరప్ మిగిలిన దేశాలని దాటి మహోధౄతంగా ముందుకు పోయింది. విజ్ఞానశాస్త్రాలు వెల్లివిరిశాయి. మూల కారణాలేమైనా దీనికి గొప్ప ఊపు నిచ్చింది వైశ్లేషిక రేఖాగణితమూ, కలనగణితమూ.
వైశ్లేషిక రేఖాగణితం (Analytical Geometry)
గణితంలో రెండు వేర్వేరు పాయలయిన రేఖాగణితాన్నీ (geometry) బీజగణితాన్నీ (algebra) కలిపి సాధింఛిన దానిని వైశ్లేషిక రేఖాగణితం అంటారు. (దీనికే కో – ఆర్డినేట్ జామెట్రీ అని కూడా పేరు.) రేఖాగణితానికి గ్రీకులూ, బీజగణితానికి మన దేశస్థులూ ఆద్యులు. బీజగణితంలో మనవాళ్ళు చేసిన కృషి గణనీయమైంది. మనం చిన్నప్పుడు ఎనిమిదో తరగతిలో బీజగణితపు లెక్కలు చేసేవాళ్ళం. ఒక్కోపువ్వు మీద రెండు తుమ్మెదలు వాలితే, ఒక పువ్వు మిగిలింది; ఒక్కో పువ్వు మీద ఒక్కో తుమ్మెద వాలితే ఒక తుమ్మెద మిగిలింది; పువ్వులెన్ని? తుమ్మెదలెన్ని? పువ్వులు x, తుమ్మెదలు y అనుకొని, సమీకరణాలు (equations) రాసి ఠకీ మని సాధించేవాళ్ళం. ఇలాంటి సమస్యలని భాస్కరాచార్యుడు లీలావతి గణితంలో ప్రముఖంగా వివరించాడు:
“విరహమల్లాటంలో పడి కొట్టుకుంటున్నప్పుడు ప్రియురాలి మెళ్ళోని ముత్యాలహారం తెగింది. ఆ ముత్యాల్లో మూడోవంతు నేలమీద, అయిదోవంతు పడకమీద, ఆరోవంతు ప్రేయసి ఒడిలో, పదోవంతు ప్రియుడి ఒడిలో పడ్డాయి. ఆరు మాత్రం దండలో మిగిలాయి. హారంలో ఉన్న ముత్యాలెన్ని?”
ఇది అడిగిన వెంటనే, చిన్న పిల్లలు కూడా, దండలోని ముత్యాల సంఖ్య x అనుకుందాము, అని మొదలెట్టి, ఓ సమీకరణాన్ని వేసి సాధిస్తారు. తెలియనిదానికి ఒక గుర్తు పెట్టడం అల్ప విషయం కాదు. సరయిన సంకేతాలు లేకపోవడం ఆలోచనకి పెద్ద అడ్డంకి. సంకేతమనేది బీజగణితానికి ఆయువులాంటిది. సంకేతాలని వాడటం మూలాన, మనం పువ్వులు, తుమ్మెదలు, ప్రియులు, ముత్యాలు – ఇలా అనేక మూర్త (concrete) భావనలనుంచి మనసుని అమూర్త (abstract) భావనల మీద కేంద్రీకరించగలం. అప్పుడు భావనలకి సార్వత్రిక యోగ్యత (universal applicability) కలిగే ఆస్కారం ఉంది. దీంట్లో మనవాళ్ళు అప్పట్లో సిద్ధహస్తులు. గ్రీకులకా జ్ఞానం లేదు. మన నుంచి బీజగణితాన్ని నేర్చుకున్న అరబ్బులు గ్రీకుల మార్గాన వెళ్ళి కొంత వెనక్కి వెళ్ళారు.
మధ్య యుగాల్లో యూరోపియన్లు అరబ్బుల మీద జరిపిన దాడుల పర్యవసానం – బీజగణితం యూరప్ చేరడం. ఇక్కడ సంకేతాల విలువని బాగా గుర్తించారు. దాంట్లో ముఖ్యపాత్ర వహించినవాడు – దే కార్ట్ (Decartes) అని పారిస్ లోనే పుట్టిన తత్వవేత్త, తత్వవేత్త కాకముందు గణితవేత్త. గణితం ద్వారానే దేవుడున్నాడని నిరూపించినవాడు!
రేఖాగణితంలోని బిందువుని (point) రెండు సంఖ్యలతో (x, y)తో గుర్తించాడు. రెండు బిందువులని కలిపే సరళరేఖని సరళ సమీకరణంతో, ఒక బిందువు కేంద్రంగా గీసే వృత్తాన్ని వర్గ సమీకరణంతో అన్వయించాడు. అలా జామెట్రీని ఆల్జీబ్రాగా మార్చేశాడు! మన జామెట్రి బాక్సులోని పరికరాలతో గీసేవన్నీ, మనం మనసులో ఈ సమీకరణాలతో ఊహించుకోవచ్చని నిరూపించి, అనేక రేఖాగణిత సమస్యలని బీజగణితం ద్వారా సులభంగా సాధించాడు. స్కేలుతో, వృత్తలేఖినితో గీయలేని రేఖాచిత్రాలని సమీకరణాలతో వివరించవచ్చని చూపెట్టాడు. ఇది విజ్ఞానశాస్త్రంలో విప్లవాత్మకైన మార్పులకి దోహదం చేసింది. బీజగణితం ఓ శక్తివంతమైన పనిముట్టుగా వృద్ధిచెందింది.
బీజగణితాన్ని రేఖాగణిత సమస్యలకి వాడినట్లుగా ఇతర సమస్యలకి కూడా వాడలేమా? అని చాలా మంది ప్రయత్నించారు. వాటిలో రెండు రకాల సమస్యలు చెప్పుకోదగ్గవి.
వంపు క్రింద వైశాల్యం (Area Under a Curve)
ఒకటి పురాతన గ్రీకుల కాలం నాటిది: త్రిభుజం, చతురస్రం, వృత్తం లాంటి క్రమాకారాల వైశాల్యాలకి సూత్రాలున్నాయి కాని నిజ జీవితంలో క్రమంగా లేని సర్వసాధారణమైన రూపాలకి సూత్రాలు లేవు. ఉదాహరణకి పొలంలో ఒకవైపు అంచు వక్రంగా ఉండొచ్చు. వంపు క్రింద వైశాల్యం (area under a curve) ఎంత? అన్నది కొన్ని వందల ఏళ్ళగా తీరని సమస్యగా ఉండిపోయింది.
ఒక మార్గమేమిటంటే, దానిని అనేక దీర్ఘ చతురస్రాలుగా (ఒక అంచు వంపుకి తాకేటట్లుగా) విభజించి, ప్రతిదాని వైశాల్యమూ కనుక్కొని వాటినన్నిటినీ కలిపొచ్చు. ఇది కచ్చితంగా కాదు కాని (ఒక అంచు వంపుకి అటూ ఇటూగా ఉండటాన), ఉజ్జాయింపుగా వస్తుంది. ఎంత కచ్చితంగా కావాలంటే అన్ని ఎక్కువ దీర్ఘచతురస్రాలుగా వాటి వెడల్పుని తగ్గిస్తూ పోవాలి. వెడల్పు అత్యంతతక్కువయితే (infinitesimal) సరయిన సమాధానం వస్తుంది.
తాత్కాలిక వేగం(Instantaneous Speed)
మరొకటి పురాతన సమస్య కాదు కాని మధ్య యుగాల్లో కనిపెట్టిన చలన సూత్రాల (laws of motion) వలన వచ్చింది. బంతిని పైకి విసిరారనుకోండి. అది కొంత వేగంతో మొదలయి, పైకి వెళ్ళి నిశ్చల స్థాయికి చేరుకొని క్రిందకు వస్తుంది కదా. దాని వేగం ప్రతి క్షణమూ (క్షణమనేది ఎంత చిన్నదయినా) మారుతూ ఉంటుంది. ఏ క్షణానయినా బంతి వేగం ఎంతో తెలుసుకోవాలంటే ఎలా? చంద్రుడి దగ్గరికి క్షేమంగా వెళ్ళి రావాలంటే ఇలాంటి జ్ఞానం లేకుండా సాధ్యం కాదు.
సమాకలన, అవకలన గణితం (Integral and Differential Calculus)
లైబ్నిట్జ్ పారిస్లో గడిపిన నాళుగేళ్ళ కాలంలో (1672-1676) ఈ రెండు సమస్యలనీ సాధించాడు. అందరినీ అప్రతిభులని చేసిన విషయం: వంపు క్రింద వైశాల్యానికీ తాత్కాలిక వేగానికీ ఉన్న అవినాభావ సంబంధం! కూడికలకీ తీసివేతలకీ ఉన్నట్లుగా ఇవి కూడా ఒకదానికొకటి విపర్యం! తాత్కాలిక వేగానికి dy/dx అని తేడా (difference) స్ఫురించేటట్లూ, వైశాల్యానికి ∫ అని సాగదీసిన S లా కూడిక (Sum) స్ఫురించేటట్లూ లైబ్నిట్జ్ సంకేతాలు నిర్దేశించాడు. ఆ సంకేతాలని కొన్ని మౌలికమైన సూత్రాలతో కలిపితే కలనగణితపు సమస్యలని బీజగణితపు సమస్యల్లాగే సులభంగా సాధించవచ్చు. యూరప్ ఖండంలో అనేకమంది రకరకాల సమస్యలకి లైబ్నిట్జ్ కలనగణితాన్ని వాడటం మొదలెట్టారు. లైబ్నిట్జ్ కెంతో పేరొచ్చింది.
(మన ప్రాచీన గణితశాస్త్రవేత్తలందరిలోకీ గొప్పవాడయిన భాస్కరాచార్యుడు కలనగణితపు ప్రాధమిక సూత్రాలని లైబ్నిట్జ్ కన్నా అయుదు వందల సంవత్సరాల ముందరే కనుక్కున్నాడు కాని వాటికి ప్రాచుర్యం రాలేదు!)
న్యూటన్తో వైరం
ఇంతలో ఒక పెద్ద సమస్య వచ్చి పడింది. న్యూటన్ ఇదే విషయాన్ని లైబ్నిట్జ్ కన్నా పదేళ్ళు ముందుగా కనుక్కున్నాడు! అయితే దానిని కొద్దిమంది మిత్రులకి మినహాయించి గోప్యంగా ఉంచాడు. నిజానికి లైబ్నిట్జ్కి రాసిన రెండు ఉత్తరాల్లో దీనిని ప్రస్తావించాడు కాని, రహస్యపు లిపిని (secret code) వాడాడు!
జర్మనీ వాడికి పేరు వస్తుందే అని ఇంగ్లాండు వాళ్ళకి కన్నుకుట్టింది. తమ న్యూటన్ అంతటి వాడికి ఎదురెవరు అని, లైబ్నిట్జ్ గ్రంథచౌర్యం చేశాడని ప్రచారం సాగించారు. న్యూటన్ రాసిన ఉత్తరాలను బయట పెట్టారు. వాటికి బదులు రాయడంలో జాప్యం జరిగింది కాని కారణం లైబ్నిట్జ్కి అవి వెంటనే చేరలేదు. ఉత్తరప్రత్యుత్తరాల మధ్య గడచిన కాలంలో న్యూటన్ అయిడియాలని లైబ్నిట్జ్ దొంగిలించి మార్చుకున్నాడని ఆరోపించారు. ఇద్దరి మిత్రులూ బాగా ఎక్కించారు. మేధావులిద్దరూ ఒకరినొకరు బహిరంగంగా దూషించుకున్నారు. పత్రికలలో ఆకాశరామన్న ఉత్తరాలు రాసి బురద చల్లారు. ఎంతైనా న్యూటన్కున్న పేరు ప్రఖ్యాతులు లైబ్నిట్జ్కి లేవు; ప్రజలు న్యూటన్ మాట నమ్మారు. లైబ్నిట్జ్ అప్రతిష్ఠ పాలయ్యాడు.
దానిని తొలగించుకోడానికి లైబ్నిట్జ్ రాయల్ సొసైటీ ఆఫ్ లండన్కి విచారణ జరపమని విజ్ఞప్తి చేసుకున్నాడు. అది సింహం గుహలో తలదూర్చడంలాగయ్యింది. న్యూటన్ అప్పుడే సొసైటీకి ప్రెసిడెంటయి ఉన్నాడు. విచారణ సంఘం వేశారు. అందులో సభ్యులందరూ న్యూటన్ మిత్రులే! “క్షుణ్ణంగా” కేసుని పరిశీలించి లైబ్నిట్జ్ ని దోషిగా తీర్మానించారు; ఓ రిపోర్టు రాశారు. రాసింది ఎవరో కాదు – స్వయానా న్యూటన్!
లైబ్నిట్జ్ చివరి దినాలు ఈ గొడవల్లో గడిచిపోయాయి. తన రాతల మూలంగా లైబ్నిట్జ్ గుండె పగిలిందని న్యూటన్ సంతోషించాడు. ఓడింది లైబ్నిట్జ్ అయినా నష్టపోయింది మాత్రం ఇంగ్లండే! న్యూటన్ విధానం గందరగోళంగా ఉంటుంది; అతనికి అర్థం అయింది కాని మిగిలిన జనాలకి అంత సులభంగా తలకెక్కలేదు. అయినా “దేశభక్తి ” పేరిట దురభిమానంతో ఇంగ్లండు అతని పద్ధతినే పట్టుకు వేలాడింది. ఒక వంద సంవత్సరాల పాటు గణితంలో వెనుకబడిపోయింది.
ఇప్పుడు ప్రపంచంలో కాలేజీలన్నిచోట్లా కలనగణితం నేర్పేది లైబ్నిట్జ్ విధానాలతోటే. ఇక్కడ గూడా మనం లైబ్నిట్జ్ లో గుర్తించాల్సిన ప్రతిభేమిటంటే, సరయిన సంకేతాలూ మౌలిక సూత్రాల ద్వారా వివిధ రంగాల్లోని క్లిష్టమైన సమస్యలకి సులభమైన సార్వత్రిక మార్గాలని కనుక్కోవడం.
లైబ్నిట్జ్ స్వప్నం
“ఏ శిల్పం? ఏ సాహిత్యం?
ఏ శాస్త్రం? ఏ గాంధర్వం?
ఏ వెల్గులకీ ప్రస్థానం?
ఏ స్వప్నం? ఏ దిగ్విజయం?”
— “దేశచరిత్రలు,” శ్రీశ్రీ.
లైబ్నిట్జ్ చిన్నప్పుడే అరిస్టాటిల్ని చదివి, మానవ వివేచన (human reasoning) ని యాంత్రికం చెయ్యవచ్చని కలలు కన్నాడు. ఇది అతనిని జీవితాంతం వదలలేదు. బీజగణితంలోని సులభ సంకేతాల, సూత్రాల ప్రాధాన్యత గ్రహించాడు. వాటిని తన ద్వియాంశపద్ధతిలోనూ కలనగణితం లోనూ వాడి విలువని చూపెట్టాడు. మానవ వ్యవహారాలలో కూడా అలాంటి అభివృద్ధి సాధ్యమని నమ్మాడు.
అందుకిలా ఆలోచించాడు: మానవ విజ్ఞానం విస్తృతంగా ఉంది. అది మనం మాట్లాడే భాషలో అనేక అర్థాలకు లోనయి తర్కించడానికి వీలుకాకుండా ఉంది. గణితంలో లాగా, మానవ వివేచనకి కూడా ఓ సార్వత్రికమైన భాషని (universal language) ప్రతిపాదించాలి. మన భావనలను ఆ భాషలో నిర్దుష్టమైన సంకేతాలతో రాయొచ్చు. ఆ భావనల మధ్యగల సంబంధాలని కూడా సూత్రీకరించొచ్చు. ఆభాషలో భ్రమతో కూడిన భావాలని రాయడం అసాధ్యం. అవివేకులు ఆభాషని వాడలేరు; వాడితే వాళ్ళూ వివేకులవుతారు! అప్పుడు మానవ వివేచన కూడా గణనం లాగే యాంత్రికం అవుతుంది. వివాదాలొచ్చినప్పుడు, కూర్చొని కాలిక్యులేట్ చేస్తే సరయిన సమాధానం వస్తుంది – సమీకరణాలు సాధించినంత సులువుగా! అదీ లైబ్నిట్జ్ స్వప్నం.
భావనలని క్రోడీకరించడం, వాటిని అనుసంధానించడానికి కావలసిన సూత్రాలను కనుక్కోవడం తనకొక్కడికే సాధ్యం కాదని లైబ్నిట్జ్ గ్రహించాడు. కొందరు విజ్ఞానవేత్తలతో ఓ అకాడెమీ పెట్టి అయిదారేళ్ళు తన ఆధ్వర్యంలో పనిచేస్తే తన కల నిజమవుతుందని ఆశించాడు. మరి వాళ్ళని పోషించేదెవరు? హానోవర్ రాజుకి గూడా దానికి కావలసిన రాబడి లేదు. లైబ్నిట్జ్ తలచుకున్నదేదైనా పట్టుదలతో సాధించాల్సిందే. హానోవర్ రాజుకి ఓ ప్రతిపాదన చేశాడు:
జర్మనీలోని హార్జ్ కొండల్లో వెండిగనులున్నాయి. ఆ గనుల తవ్వకం మీద రాజుకి కొంత రాబడి వస్తుంది. గనులు చాలా లోతుగా ఉండి ఊట పడేది. ఆ ఊటని తోడి బయటపడెయ్యడానికి పంపులు వాడేవాళ్ళు. ఆ పంపులు నీళ్ళ చక్రాల ఆధారంగా నడిచేవి. నీళ్ళు కొండ వాగులనుండి వచ్చేవి. అయితే శీతాకాలంలో సెలయేళ్ళన్నీ గడ్డకట్టుకుపోయి పంపులు పనిచెయ్యక తవ్వకం పనులు మూతపడేవి; రాబడి తగ్గేది.
ఏడాది పొడుగూ పనిచేసే యంత్రాంగం ఉంటే, రాబడి పెరుగుతుందన్న ఆలోచన లైబ్నిట్జ్కి వచ్చింది. ఏడాది పొడుగూ వాతావరణం ఎలాగున్నా లభ్యమయ్యేదేమిటి? గాలి! పంపుల్ని గాలిమరలతో (windmills) తో నడపాలని నిర్ణయించాడు. హానోవర్ రాజుని ఒప్పించి తను సొంతంగా పెట్టుబడి కూడా పెట్టాడు. అయితే గాలి అన్ని వేళలా అనుకూలించకా, ఆ టెక్నాలజీ ఇంకా శైశవస్థాయిని దాటకా, ప్రాజెక్టు సఫలం కాలేదు. అయిదారేళ్ళ తర్వాత చాలా నష్టం కలిగి, ఇక భరించలేక స్వస్తి చెప్పాల్సొచ్చింది.
ఇంతగా విఫలమయిన ప్రాజెక్టులో కూడా లైబ్నిట్జ్ గనుల గురించీ, నాణాల గురింఛీ పరిశోధనలు చెయ్యడమే కాక, భూగర్భశాస్త్రం గురించి మౌలికమైనవి కనుగొన్నాడు. భూమి ఎలా ఏర్పడిందో, జీవరాశి ఎలా వచ్చిందో – వీటి గురించి అతని ఊహాగానాలు చదివితే, అతని అసమాన ప్రతిభా వైవిధ్యం ఎలాంటిదో తెలుస్తుంది.
సార్వత్రిక భాష గురించి లైబ్నిట్జ్ పెద్దగా వివరాలు ఇవ్వలేదు కాని, భావనలని సంధానం చెయ్యడానికి కావలసిన కలనగణితం గురించి కొన్ని ప్రతిపాదనలు చేశాడు. బీజగణితంలో కొన్ని సూత్రాల ఆధారంగా సమీకరణాలని వేర్వేరు రూపాల్లోకి మార్చి (manipulate) సాధిస్తాము. తార్కిక భావనలకి కూడా అలాటి సూత్రాలని కనుక్కోడానికి కొంత కృషి చేశాడు.
అనేక భావాల సముదాయాలు (collections), A, B తీసుకుందాం. ఈ రెండింటినీ కలిపితే వచ్చే సముదాయాన్ని C అంటే, A⊕B=C. దీనిని ఏ క్రమంలోనయినా చెయ్యొచ్చు. అంటే A⊕B=B⊕A. ఇది మనకి సంఖ్యాగణితంలో పరిచయమే – 2+3=3+2 కదా. కాని ఒక సముదాయాన్ని దానితో కలిపితే వచ్చేది అదే సముదాయం. అంటే A⊕A=A. ఒక భావనని దానితో కలిపితే కొత్త భావనలేమీ రావు కదా. ఇది సంఖ్యాగణితం కన్నా తేడాగా ఉందని (2+2=4)గమనించాలి. ఆ తేడా చూపడానికే + వాడకుండా కొత్త గుర్తు ⊕ ని వాడాడు.
ఇది ప్రతీక తర్కానికి (symbolic logic) నాంది అనుకోవచ్చు. కాని దీనిని మరో ఒకటి రెండు వందల సంవత్సరాల దాకా పట్టించుకున్న నాథుడు లేడు.
అవధుల్లేని ఆశావాదం
“జీవితం దేవతల దరస్మితం
చిన్నారీ! పెదవిమీద సింగారించు
కలతవద్దు కొలతవద్దు
అలసట అలజడివద్దు బాల!
అపుడు
బ్రతుకే లలిత లలిత లతాంతమాల.”
— “చిన్నారికి చిన్నమాట,” బాలగంగాధర తిలక్.
మానవ వివేచన అనేది ఎంతో విస్తృతంగానూ వైవిధ్యంగానూ ఉంది గదా. దానిని ఏవో నాలుగు కొత్త గణితసూత్రాలతో కట్టుదిట్టం చెయ్యడానికి సాహసించడం హాస్యాస్పదం అనిపించవచ్చు. కాని లైబ్నిట్జ్ గణితవేత్తే కాక పేరున్న తత్వవేత్త కూడా. నిర్దిష్టమైన ప్రాపంచిక దృష్టి కలవాడు.
లైబ్నిట్జ్ ఈ విశ్వసృష్టికి కారణం విశ్వానికి వెలుపలే కాని లోపల కనుక్కోలేమన్నాడు. దానినే దేవుడన్నాడు. విశ్వకర్తగా దేవుడు ఈ ప్రపంచాన్ని ఏవిధంగానయినా సృష్టించవచ్చు కాని ఇలాగే సృష్టించడానికి తగిన కారణం (sufficient reason) ఉండి ఉండాలి. లేకపోతే దేవుడు ఇలా సృష్టించాల్సిన అవసరం లేదు. ఈ విశ్వంలో ప్రతిదీ గతంలో నిర్ణయించిన సామరస్యాన్ని (pre-established harmony) బట్టి నడుస్తుంది – శివుడి ఆజ్ఞ లేనిదే చీమన్నా కదలదన్నట్లుగా. ఆజ్ఞ ముందే నిర్ణయించిన ప్రకారం ఉంటుంది కనుక మనం దానిని బుద్ధి చింతన ద్వారా తెలుసుకోవచ్చన్నది లైబ్నిట్జ్ విశ్వాసం. ఆ విధంగా చూస్తేకాని, వివేచనని యాంత్రికం చెయ్యొచ్చనన్న అతని ఆశావాదాన్ని అర్థం చేసుకోలేము.
దేవుడే సృష్టిస్తే, ఇలాగే ఎందుకు సృష్టించాడు, మరోలా ఎందుకు సృష్టించలేదు అన్న ప్రశ్న వస్తుంది. ఇంతకన్నా మంచిది లేదు కనుక అని సమాధానం. ఇదే ఉత్తమమైన విశ్వం (The best of all possible worlds) అయితే ప్రపంచం ఇంత పాపభూయిష్టంగా ఎందుకుంది? అన్నదానికి చెడు లేకపోతే మంచి విలువ తెలియదని సమాధానం. మండుటెండలో దాహంతో బాధపడితేనే గదా చల్లని నీళ్ళ విలువ తెలిసేది!

“అంతా మన మంచికే” అన్న ఈ “ఆశావాదం” లైబ్నిట్జ్ తర్వాత యూరప్లో పరాకాష్టకు చేరుకుంది. దానిని తూర్పారపడుతూ, వోల్టేర్ ఓ గొప్ప నవల, కాన్డీడ్ (Candide), రాశాడు. దాంట్లో ప్రొఫెసరు పాన్గ్లాస్ (Pangloss) పాత్ర లైబ్నిట్జ్ని వ్యంగ్యంగా చిత్రించడానికే.
“మై డియర్ పాన్గ్లాస్! నీకు ఉరిశిక్ష వేసి, నిర్దాక్షిణ్యంగా కొరడా దెబ్బలు వేసి, చిత్రవధల పాల్చేశారు. అయినా ఈ ప్రపంచంలో అంతా మన మంచికే జరుగుతుందంటావా?” అని విస్మయపడతాడు కాన్డీడ్.
“నేను తత్వవేత్తని. నా సిద్ధాంతాల్ని మాటిమాటికీ మార్చుకోను. లైబ్నిట్జ్ తప్పు కావడానికి ఆస్కారం లేదు. దేవుడు ముందుగానే సృష్టించిన సామరస్యానికన్నా ప్రపంచంలో మించింది లేదు,” అని నిబ్బరంగా చెప్తాడు పాన్గ్లాస్.
ఈ శుష్కవాదాలకి విసిగెత్తిన కాన్డీడ్, “అద్భుతంగా చెప్పావు. ఇక పోయి తోటపని చేసుకుందాం,” అనడంతో నవల ముగుస్తుంది.
అయితే లైబ్నిట్జ్ శుష్కవాదాప్రియుడు కాదు; క్రియావాది. తోటపని చేసే ముందు ఏ మొక్కలు నాటాలో విచారిద్దాం; అందుకు వివాదాలవసరం లేదు; మొక్కల గురించిన సమాచారం సేకరించి, కలనయంత్రం ముందు కూర్చుందాం, “Let us calculate and we will know the answer,” అంటాడు. మరి లైబ్నిట్జ్ స్వప్నం సఫలవుతుందా లేదా అన్నది ముందు సంచికలలో తెలుసుకుందాం.
చదవదగ్గ పుస్తకాలు
నేనీ వ్యాసం రాయడానికి ఉపయోగించుకున్న పుస్తకాల్లో కొన్నిటి వివరాలు:
- Master of All Trades, in Men of Mathematics, by E. T. Bell. Simon & Schuster. 1937. ఇది చాలా పాత పుస్తకమయినా, చారిత్రకంగా తప్పులున్నా, కొన్నిచోట్ల మితిమిమీరిన కల్పనలున్నా, ఇప్పటికీ చదివేవాళ్ళలో గణితమంటే ఉత్తేజం కలగజేస్తుంది. కొందరు ప్రపంచ ప్రఖ్యాతి గాంచిన గణిత శాస్త్రజ్ఞులు తాము హైస్కూల్లో ఈ పుస్తకాన్ని చదివే స్ఫూర్తి పొందామన్నారు. మొదటి అధ్యాయం పురాతన గ్రీకులతో మొదలయి రెండో అధ్యాయం పదిహేడో శతాబ్దంలోకి గెంతుతుంది! యూరోపియన్లే దీంట్లో నాయకులు.
- Leibniz’s Dream, in The Universal Computer: The Road from Leibniz to Turing, by Martin Davis. W. W. Norton Company. 2000. గత యాభై ఏళ్ళలో కంప్యూటర్లు ఎవరూ ఉహించనంతగా అభివృద్ధి చెందాయి. అందుకు నిస్సందేహంగా అభినందిచాల్సింది కంప్యూటర్ ఇంజనీర్లనే. కాని 1950నాటి హాలునాక్రమించే కంప్యూటర్లు మొదలుకొని ఇవాళ్టి సెల్ఫోన్, లాప్టాప్, సూపర్ కంప్యూటర్ దాకా, అన్నీకూడా ఒకే రకమైన లాజిక్ మీద ఆధారపడినవే! అది గత మూడొందల సంవత్సరాలలో కొందరు తార్కికుల అమోఘ మేధాపటిమ చలవ. వాళ్ళ జీవితాలనీ, ఆలోచనలనీ ప్రముఖ తార్కికుడు Davis ఈ పుస్తకంలో ప్రశంసనీయంగా వర్ణించాడు.
- Leibniz: A Biography, by E. J. Aiton. Bristol. 1985. ఇది సాధికారికమైన లైబ్నిట్జ్ జీవిత చరిత్రే కాని, పండితులని దృష్టిలో పెట్టుకొని రాసినట్లనిపించింది.
- Life of Godfrey William von Leibniz, by Milton Mackie. 1845. On the basis of German Work by Gottschalk E. Guhrauer. ఇది చదవడానికి సులభంగా ఉంది. ఇంటర్నెట్లో ఉచితంగా దొరుకుతుంది.
- Leibniz, in The History of Western Philosophy, by Bertrand Russell. Simon & Schuster. 1972. పాశ్చాత్య తత్వచింతనని సమాజం నుండి విరహితులైన కొందరు వ్యక్తుల తలపోతలగా కాక, సమకాల పరిస్థితులకి స్పందనలగా చిత్రించిన గ్రంథం.
- Issac Newton, by James Gleick. Pantheon Boks. 2003. “I don’t know what I may seem to the world, but, as to myself, I seem to have been only like a boy playing on the sea-shore…” అన్నది అందరం విన్నదే. “సదా బాలకుడి” గురించి ఇంకా లోతుగా తెలుసుకోడానికి ఇది చదవచ్చు.
- Number: The Language of Science, by Tobias Dantzig. The Masterpiece Science Edition. Pi Press, New York. 2005. “లెక్కల పరిణామం మీద ఇంతకన్నా మంచి పుస్తకం లేదు,” అని ఐన్స్టయిన్ పొగిడాడు. మొదటి ప్రచురణ 1930లో! సంఖ్యాచరిత్ర మీద ఇది క్లాసిక్. ప్రతీకల ప్రాముఖ్యతని “Symbols” అధ్యాయంలో చక్కగా వివరించాడు. లీలావతి గణితంలోని సమస్య దాంట్లో ఉదహరించిందే.
- The Crest of the Peacock: Non-European Roots of Mathematics by George Gheverghese Joseph. Penguin Books. 2000. యూరప్ బయటవాళ్ళు గణితంలో చేసిన కృషిని వివరించే పుస్తకం. మన దేశం సాధించిన విషయాల మీద రెండు అధ్యాయాలున్నాయి. “నెమలి పింఛంలాగా, సర్పశిఖామణిలాగా, గణితం అన్ని శాస్త్రాలకీ తలమానికమైనది,” అన్న వేదాంగ జ్యోతిషం నుండి ఈ పుస్తకం పేరు తీసుకున్నారు. (దీనికి మూలం “యథా శిఖా మయూరాణాం నాగానాం మణయో యథా | తథైవ సర్వశాస్త్రాణం జ్యౌతీషం మూర్ధాని స్థితం,” జ్యోతిష వేదాంగ, 100 B.C. – సంపాదకులు.)
- The History of Ancient Indian Mathematics by C.N. Srinivasiengar. ప్రాచీన భారత గణితశాస్త్రం గురించిన విలువైన పుస్తకం. గణిత వివరణలూ, సమీకరణాలూ ఆసక్తి లేవని దాటేసినా, మన చరిత్ర కోసమయినా ఈ పుస్తకం చదివి ఆనందిచవచ్చు.
- “జగమంతా శక్తి స్వరూపంగా దర్శించిన లైబ్నిట్జ్” అధ్యాయం, విశ్వదర్శనం: పాశ్చాత్య చింతన, పుస్తకంలో. నండూరి రామమోహనరావు. పల్లవీ పబ్లికేషన్స్. 2002. తెలుగులో పాశ్చాత్య చింతనని పరిచయం చేసిన చెప్పుకోదగ్గ పుస్తకం.

