1. ఉపోద్ఘాతం

పైసా ఖర్చు లేకుండా మిలియన్ డాలర్లు సంపాదించే ఉపాయం చెబుతాను, వింటారా?

అంత తేలికైతే నువ్వే ఆ ఉపాయం వాడుకోవచ్చు కదా? అని మీరడగచ్చు.

తేలిక అనలేదు. ‘పైసా ఖర్చు లేకుండా’ అన్నాం. లాటరీ టికెట్టు కొనక్కరలేదు, వేగస్ వెళ్ళి వేలు తగలేసుకు రానక్కరలేదు. కడుపులో చల్ల కదలకుండా ఇంట్లో కూర్చుని సంపాదించే ఉపాయం. చెప్పమన్నారా? అయితే వినండి. రీమాన్ ఉటంకించిన శిష్టాభిప్రాయం (conjecture) ఒప్పే అని రుజువు చేస్తే క్లే మేథమేటికల్ ఇన్స్టిట్యూట్ (Clay Mathematical Institute) వారు బిళ్ళ కుడుముల్లాంటి మిలియను డాలర్లు పట్టుకొచ్చి ఒళ్ళో పోస్తామని 2000లో ప్రకటన చేసేరు.

ఇక్కడ శిష్టాభిప్రాయం అనే కొత్త మాట వాడేను – పొందికైన, శాస్త్రానుగుణమైన ఊహ, అని అభిప్రాయం. ఏమిటా శిష్టాభిప్రాయం?

జీటా ప్రమేయం (zeta function) యొక్క శూన్యాలు లేదా సున్నాలు (zeros), లేదా మూలాలు (roots) అన్నీ (నిజ, రుణ రేఖ మీద కనబడే సాధారణ మూలాలని మినహాయించి) సంకీర్ణ లేదా జంట తలంలో (అనగా, complex planeలో) x = ½ అనే రేఖ మీదే గుమిగూడి ఉన్నాయి —

అని రుజువు చెయ్యాలి. ఇది నిజమే సుమా అని రీమాన్ ఒక అమూల్య అభిప్రాయం వెలిబుచ్చేడు, రుజువు చెయ్యకుండా! మనకి ఇప్పుడు ఆ రుజువు కావాలి. ఈ అభిప్రాయం నిజమే అని రుజువు చేసిన వారికి మిలియను డాలర్లు బహుమానం ఇచ్చేస్తారు. అంతటితో పురస్కార పరంపర ఆగిపోదు. ఏదో పెద్ద విశ్వవిద్యాలయం వారు ఆచార్య పదవి అంటగడతారు. ‘నీ తెలివిని, నా అందాన్ని పుణికిపుచ్చుకుని పిల్లలు పుట్టొచ్చు కదా’ అని హా(బా)లివుడ్ తార పెళ్ళి ప్రతిపాదిస్తే, మిలియను డాలర్లతో పాటు స్వర్గ ద్వారాలు కూడ తెరుచుకోవచ్చు!

సమస్య చెప్పేసి పారిపోతే ఏం మర్యాదగా ఉంటుంది? పరిష్కారానికి దారి కూడ చూపాలి కదా! ఏ పుట్టలో ఏ పాము ఉందో?

1. హిల్బర్ట్ అభిప్రాయం

ఏ సంఖ్య అయినా 1 చేత, తన చేత తప్ప మరే ఇతర సంఖ్య చేత నిశ్శేషంగా భాగహారానికి లొంగక పోతే ఆ సంఖ్యని ప్రధాన సంఖ్య అంటారు (1ని మినహాయించి.) కనుక 2, 3, 5, 7, 11, 13 వగైరాలు అన్నీ ప్రధాన సంఖ్యలకి ఉదాహరణలు అని చెప్పి ప్రారంభిస్తాను. ఇక్కడ నుండి అంచెలంచెల మీద లోతుకి తీసుకు వెళతాను. గణితంలో సంప్రదాయికంగా వాడే సంకేతాలతో పరిచయం ఒక మోతాదు, కలన గణితంతో పరిచయం ఒక మోతాదు, ఇనుమడించిన ఉత్సాహం ఒక మోతాదు ఉంటే ఇక్కడ చెప్పేది అర్థం చేసుకుందుకి పెద్దగా పాండిత్యం అక్కరలేదు. సమస్య అర్థం అయిన తరువాత, దానిని పరిష్కరించి, మిలియను డాలర్లు కొట్టేయడానికి కొంచెం లోతుగానే పాండిత్యం ఉండాలి – ఎందుకంటే ఇది చాల జటిలమైన సమస్య; అంత తేలికగా లొంగదు. బొమ్మ.1 రీమాన్ వెలిబుచ్చిన శిష్టాభిప్రాయం యొక్క ప్రాముఖ్యతని గుర్తిస్తూ డేవిడ్ హిల్బర్ట్(David Hilbert) ఉటంకించిన అభిప్రాయం.(రీమాన్ వాడిన హైపాథసిస్ అన్న మాట ఇక్కడ వాడుతున్న కంజెక్చర్ అన్న మాట దరిదాపుగా సమానార్థకాలే.)

2. చారిత్రక నేపథ్యం

శ్రీమాన్ రీమాన్ గురించి ఒక మాట. గెయార్క్ ఫ్రీడ్రిక్ బేర్న్‌హార్ట్ రీమాన్ (Georg Friedrich Bernhard Riemann, September 17, 1826 – July 20, 1866) తన 28వ ఏట, అనగా 1854లో, చేసిన ప్రసంగాన్ని ఆధారంగా చేసుకుని ఐన్‌స్టయిన్ తన సార్వత్రిక సాపేక్ష సిద్ధాంతం (General Theory of Relativity) అనే మహా సౌధాన్ని లేవనెత్తేడు. గణితంలో రీమాన్ అంతటి దిట్ట. అదే వ్యక్తి అయిదేళ్ళు పోయిన తరువాత, 1859లో కేవలం పది పుటలు పొడుగున్న ఒక పరిశోధనా పత్రాన్ని ప్రచురించి గణిత ప్రపంచాన్ని అదరగొట్టేడు. ఆ పత్రంలోనే ఆయన తన శిష్టాభిప్రాయాన్ని వెలిబుచ్చేడు. చిత్రం ఏమిటంటే సంఖ్యాశాస్త్రంలో (Number Theory) ఆయన రాసిన ఏకైక పరిశోధనా పత్రం ఇది.

2. బేర్న్‌హార్ట్ రీమాన్

అప్పటికే ఎంతో పేరు మోసిన ప్రధాన సంఖ్యా సిద్ధాంతం (The Prime Number Theorem) మీద ఈ శిష్టాభిప్రాయం ఎంతో ప్రభావం చూపడం వల్ల, ఈ సమస్యని పరిష్కరించవలసిన అవసరం కీలకం అయి కూర్చుంది. ఈ ప్రధాన సంఖ్యా సిద్ధాంతానికి పెద్ద ప్రవరే ఉంది. ఇచ్చిన ఒక ‘సరిహద్దు’ సంఖ్య xని మించకుండా ప్రధాన సంఖ్యలు ఎన్ని ఉన్నాయో ఊహించి ఉరమరగా చెబుతుంది ఈ సిద్ధాంతం. ఈ ఉరమర మద్దింపుకి ఏడ్రియెన్ లెజాండర్ (Adrien-Marie Legendre) ఒక సూత్రాన్ని ఇస్తే దానిని కాసింత మెరుగు పరచి ఫ్రీడ్రిక్ గౌస్ (Johann Carl Friedrich Gauss) తన 18వ ఏట మరొక సూత్రాన్ని ప్రవచించేడు. నిజరేఖ (real line) మీద ఒక హద్దుని ఇస్తే, ఆ హద్దుని మించకుండా ఆ రేఖ మీద ఎన్ని ప్రధాన సంఖ్యలు ఉంటాయో ఉరమరగా చెబుతుంది ఈ సూత్రం. గౌస్ అంచనాని మరింత మెరుగు పరచి రీమాన్ (గౌస్ శిష్యుడు) మరొక సూత్రం ఇచ్చేడు. ఈ సూత్రం పని చేస్తున్నట్లే ఉంది కాని పునాదులు ఎంత దిట్టంగా ఉన్నాయో తెలియదు. పునాదులు దిట్టంగా ఉండాలంటే రీమాన్ వెలిబుచ్చిన శిష్టాభిప్రాయం నిజం అవాలి. అప్పుడు ఉరమర లెక్కలో దోషం (error) ఎంత ఉందో లెక్క కట్టవచ్చు.

ముందుకి కదిలే ముందు, ఇక్కడ మనకి కావలసిన అవసరాల మేరకి, ప్రమేయం (function) అంటే ఏమిటో చెప్పనివ్వండి. ప్రమేయం ఒక పెట్టె లాంటిది. ఈ పెట్టెకి ఒక పేరు ఉంటే బాగుంటుంది కదా. సర్వసాధారణంగా, ఇంగ్లీషు ప్రపంచంలో, ఇటువంటి పెట్టెకి f అనే పేరు పెడతారు. ఈ పెట్టె లోనికి మనం x అనే అంశాన్ని పంపితే ఈ పెట్టె మరొక అంశాన్ని బయటకి వెలిగక్కుతుంది – అది ఈ పెట్టె లక్షణం. ఈ ప్రక్రియని గణిత పరిభాషలో f(x) అని రాస్తారు. అంటే – f అనే పెట్టెలోకి x అనే సంఖ్యని పంపితే బయటకి f(x) అనే సంఖ్య వస్తుంది – అని అర్థం. ప్రమేయం గురించి ఇంతకంటె లోతుగా తెలుసుకోవలసిన అవసరం లేదు.

ఇప్పుడు లెజాండర్-గౌస్ నిర్మించిన సూత్రాన్ని వాడడం ఎలాగో చూద్దాం. ఉదాహరణగా x అనే హద్దు పెడదాం. ఈ xని మించకుండా ఎన్ని ప్రధాన సంఖ్యలు ఉన్నాయో ఆ సంఖ్యని n(x) అనే ప్రమేయంతో సూచిద్దాం. దిగువ పట్టిక చూడండి. ఈ n(x) ఉరమరగా x/ ln x అంత ఉంటుంది అన్నాడు లెజాండర్. మచ్చుకి x = 100 అయితే, 100/ ln 100 = 21.7 కనుక 100 లోపున ఉరమరగా 22 ప్రధాన సంఖ్యలు ఉంటాయని ఈ సూత్రం అంచనా వేస్తోంది. నిజానికి 100 లోపున 25 ప్రధాన సంఖ్యలు ఉన్నాయి (లెక్క వేసి చూసుకొండి). కనుక ఈ అంచనాలో దోషం 22 – 25 లేదా 3శాతం. మరొక మచ్చుగా, హద్దు x = 1,000,000,000 అయితే మన అంచనా 10⁹/ ln 10⁹ = 48,254,942. నిజానికి బిలియను హద్దు లోపున 50,847,534 ప్రధాన సంఖ్యలు ఉన్నాయి (ఇది మీరు లెక్క వేసి చూసుకోలేరు కాబట్టి నా మాట నమ్మండి.) కనుక లెజాండర్ అంచనాలో దోషం 48,254,942 – 50,847,534 = -2,592,592 లేదా 2,592,592 / 1,000,000,000x 100 = 0.25శాతం. ఈ లెజాండర్ లెక్కని గౌస్ మెరుగు పరచేడు. నిజ రేఖ మీద దూరం వెళుతూన్న కొద్దీ గౌస్ అంచనా మెరుగవుతుంది. ఇదే లెక్కని రీమాన్ శిష్టాభిప్రాయం చెప్పిన పద్ధతిలో చేస్తే దోషం ఎంత ఉంటుందో కూడ ఈ దిగువ పట్టికలో చూడవచ్చు.

x	n(x)	లెజాండర్ దోషం	గౌస్ దోషం	రీమాన్ దోషం
10	4	0	2	–
102	25	-3	5	1
103	168	-23	10	0
106	78498	-6116	130	29
109	50847534	-2592592	1701	-79

రీమాన్ శిష్టాభిప్రాయమే రుజువయితే, రీమాన్ ఇచ్చిన సూత్రసమీకరణాలు (formulae) ఉపయోగించినప్పుడు – అనగా, ఉదాహరణకి, పది కోట్ల లోపు ఎన్ని ప్రధాన సంఖ్యలు ఉన్నాయి? పదివేల నూటపదహారవ ప్రధాన సంఖ్య ఏది? వంటి ప్రశ్నలకి జవాబులు లెక్క కట్టినప్పుడు – మనకి ఆమోదయోగ్యమైన దోషాలకి లోబడే జవాబులు వస్తున్నాయని నూటికి నూరు శాతం నమ్మవచ్చు. అదీ రీమాన్ శిష్టాభిప్రాయం ప్రాముఖ్యతకి కారణం.

ఈ శిష్టాభిప్రాయం ఒక అభిప్రాయంలా ఉండిపోయింది; పకడ్బందీగా ఉన్న రుజువు లేక ఒక సిద్దాంతం స్థాయికి ఎదగలేదు. అయితేనేం? గణిత శాస్త్రవేత్తలు ఈ అభిప్రాయం నిజమే అయి ఉంటుందని ఎంతగా నమ్ముతున్నారంటే దరిదాపు 500 సిద్ధాంతాలు (theorems) ‘రీమాన్ శిష్టాభిప్రాయమే కాని నిజమయితే…’ అంటూ మొదలవుతాయిట. కనుక ఈ శిష్టాభిప్రాయానికి కాని రుజువు సంపాదించగలిగితే ఒక్క దెబ్బలో వందలకొద్దీ సిద్దాంతాలని రుజువు చేసెయ్యవచ్చు. అనగా, పునాదులు లేకుండా గాలిలో కట్టేస్తున్న మేడలకి పునాదులు నిర్మించడం అన్న మాట.

మరొక ఆసక్తికరమైన కోణం ఉంది. రీమాన్ అభిప్రాయం నిజమా కాదా అనే విషయం కన్న (ఇది నిజమే అయుంటుందని అందరూ నమ్మేస్తున్నారు కాబట్టి) దీన్ని రుజువు చేసే ప్రక్రియ అంటూ ఉండుంటే ఆ ప్రక్రియ, ఆ పద్ధతి (సిద్ధాంతం రుజువు మాట దేవుడెరుగు) గణితశాస్త్రపు లోతులలో ఉండే ఒక మౌలికమైన ‘దర్శనం’ లాంటిది అవుతుందని శాస్త్రవేత్తలు విశ్వసిస్తున్నారు. అప్పుడు ఆ దారి వెంబడి వెళితే ఎన్నో నూతన అంశాలని ఆవిష్కరించడానికి వీలు అవుతుందనీ వారి ఆశ. ఉదాహరణకి, ఎంత పెద్ద సంఖ్యకి అయినా ప్రధాన భాజకాలు (prime factors) కనుక్కోవడమనే చాల కష్టమైన పని సుళువు అవుతుందని ఒక ఆశ. అప్పుడు కంప్యూటర్ రంగంలో రహస్య లిపిలో దత్తాంశాలని పంపే పద్ధతులలో మౌలికమైన మార్పులు రావచ్చు.

3. రీమాన్ జీటా ప్రమేయం

ఇప్పుడు మళ్ళా మన ప్రమేయం అనే పెట్టె వద్దకి వద్దాం. సర్వసాధారణంగా పెట్టె లోపల ఏమి జరుగుతోందో చెప్పడానికి ఒక సమీకరణం వాడతారు. ఉదాహరణకి f(x) = x² అని చెప్పేమనుకుందాం. దీని అర్థం ఏమిటంటే పెట్టెలోకి xని పంపితే, పెట్టె x²ని బయటకి వెలిగక్కుతుంది. ఇంకా వివరంగా చెప్పాలంటే x = 1 అయితే పెట్టె బయటకి 1² = 1 వస్తుంది, x = 2 అయితే పెట్టె బయటకి 2² = 4 వస్తుంది, x = 3 అయితే పెట్టె బయటకి 3² = 9 వస్తుంది. పెట్టె లోపలికి నిజ సంఖ్యలే వెళ్ళనక్కర లేదు; కాల్పనిక సంఖ్యలు (imaginary numbers) కూడ వెళ్ళవచ్చు; x = i అనే కాల్పనిక సంఖ్య అయితే పెట్టె బయటకి i² = -1 అనే నిజ సంఖ్య వస్తుంది.

రీమాన్ తను వాడిన ప్రమేయానికి జీటా ఫంక్షన్ ζ(s) అని పేరు పెట్టేడు. ఈ వింత ఆకారంలో ఉన్న అక్షరం గ్రీకు భాషలోని జీటా (ఇది దంత్య జ: ౙ) అనే అక్షరం. ఇక్కడ s అనేది జంట సంఖ్యని (complex number) సూచిస్తుంది. కనుక ఈ జీటా ఫంక్షన్ అనే పెట్టె లోకి a + bi అనే జంట సంఖ్యని పంపితే బయటకి c + di అనే మరొక జంట సంఖ్య వస్తుంది. కొద్ది సేపట్లో రీమాన్ పేరు మీదుగా ఉన్న ఈ జీటా ఫంక్షన్ రూపం రాసి చూపెడతాను. రీమాన్‌కి ముందు ఆయ్‌లర్ (Euler) ఇదే రకం ప్రమేయాన్ని వాడి ఉన్నాడు; ఆయ్‌లర్ ప్రమేయంలో చలనరాశి ఎల్లప్పుడూ నిజ సంఖ్య (real number) x మాత్రమే. ఈ తేడా నొక్కి వక్కాణించడానికి ఆయ్‌లర్ వాడిన ప్రమేయాన్ని Z(x) అని రాస్తారు. ఆయ్‌లర్ Z వాడేడు కనుక రీమాన్ ζ వాడి ఉంటాడు. జీటా ప్రమేయం ζ(s)లో s విలువ జంట సంఖ్య (complex number.) ఈ చరిత్రని పురస్కరించుకుని రీమాన్ జీటా ప్రమేయాన్ని ఆయ్‌లర్-రీమాన్ జీటా ప్రమేయం అని కూడ అంటారు. ఇటుపైన, సౌలభ్యం కొరకు, Z(x) – ζ(s)ల మధ్య ఉన్న తేడా – మౌలికమైనదే అయినా – పట్టించుకోకుండా కథ నడిపిద్దాం. (గణితలోక పండితులు మనలను క్షమింతురు గాక!)

ఆయ్‌లర్ ప్రమేయాన్ని, రీమాన్ జీటా ప్రమేయాన్ని గణిత భాషలో రాసినప్పుడు – జంట తలంలో ఎక్కడ ఉన్నామో దానిని బట్టి – ఎన్నో రూపాలలో రాయవచ్చు. కొన్ని రూపాలు తేలికగా అర్థం అవుతాయి, కొన్ని గభీమని అర్థం కావు. వీటిలో తేలిక రూపం చూసే ముందు, ఈ ప్రమేయం ఈ దిగువ చూపించిన విధంగా, అనగా, కొన్ని రాశుల మొత్తంగా, ఉంటుందని ఊహించుకోవచ్చు:

ζ(s) = a + b + c + …

ఇదే ప్రమేయాన్ని కొన్ని రాశుల లబ్దంగా, అనగా – ఈ కింది విధంగా, కూడ రాయవచ్చని ఆయ్‌లర్‌కి తోచింది:

ζ(s) = (A).(B).(C)…

ఇలా తిరగ రాసినప్పుడు A, B, C, …, వంటి రాశులలో ‘ప్రధాన సంఖ్యల శ్రేణులు’ వచ్చేటట్లు చెయ్యవచ్చని ఆయ్‌లర్‌కి తట్టింది. అంటే జీటా ప్రమేయానికి ప్రధాన సంఖ్యలకి మధ్య ఏదో అవినాభావ సంబంధం ఉన్నట్లే కదా! ఆయ్‌లర్‌ చేసిన ఈ గమనిక ప్రధాన సంఖ్యల పరిశోధనలో ఒక కీలక ఘట్టం అయింది. జీటా ప్రమేయపు అనంత శ్రేణిలో ప్రధాన సంఖ్యల లబ్దాలు అంతర్గతంగా ఇమిడి ఉన్నాయనే విషయమే ఆయ్‌లర్‌ నిర్వచించిన Z(x) అనే ప్రమేయాన్ని తీసుకుని, సంస్కరించి, ζ(s) అని రాయాలనే కోరికని రీమాన్‌కి పుట్టించిందని మనం చెప్పుకోవచ్చు.

ఉదాహరణకి రీమాన్ జీటా ప్రమేయాన్ని, ఒక విధంగా రాస్తే, 3వ బొమ్మలో చూపెట్టినట్లు కనబడుతుంది.

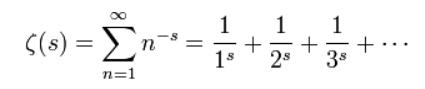
3. ఒక అవతారంలో రీమాన్ జీటా ప్రమేయం

ఇక్కడ s అనేది జంట చలనరాశి (complex variable). అంటే, s = a + bi లా ఉంటుంది. ఇందులో a అన్నది నిజ అక్షం మీద దూరం, b అన్నది కల్పన అక్షం మీద దూరం.

ఇప్పుడు జీటా ప్రమేయం యొక్క ప్రవర్తన అర్థం చేసుకోడానికిగాను sకి రకరకాల విలువలు ఇచ్చి ఈ ప్రమేయం విలువలు కట్టి చూద్దాం.

ఉదాహరణకి s = 1 అయితే –

ζ(1) = 1/1 +1/2+ 1/3 + 1/4 + …

కళాశాలలో మొదటి సంవత్సరం లెక్కల విద్యార్ధిని ఎవ్వరిని అడిగినా పైన చూపిన శ్రేణిని (లేదా శ్రేఢిని) హరాత్మక శ్రేణిగా (harmonic series) గుర్తు పట్టి దాని మొత్తం అనంతం (∞) అవుతుందని చెప్పగలడు. అనగా జీటా ప్రమేయానికి s = 1 దగ్గర అస్తిత్వం లేదు. శూన్యస్థానాన్ని ఇంగ్లీషులో జీరో (zero) అన్నట్లే ఈ s = 1 అనే బిందువు సూచించే అనంత స్థానాన్ని ఇంగ్లీషులో పోల్ (pole) అని అంటారు. రెండింటిని తేలికగా శూన్యాలు, అనంతాలు (zeros and poles) అంటారు.

మరొక ఉదాహరణగా s = 2 అయితే, ζ(2) = (π * π)/6 అవుతుందని రుజువు చెయ్యవచ్చు. ఆయ్‌లర్ ఇచ్చిన రుజువు పాఠ్య పుస్తకాలలో దొరుకుతుంది. నిజానికి s విలువ 1 కానంత సేపూ ζ(s) విలువ ఇంత అని నిర్ధారించడం పెద్ద కష్టం కాదు.

మరొక ఉదాహరణగా s = – 2 అయితే ζ(-2) = 0 అవుతుందని రుజువు చెయ్యవచ్చు. నిజానికి s విలువ -2, – 4, – 6, … అయినంత సేపూ ζ(s) విలువని ‘సున్న’ అని నిర్ధారించడం కూడ పెద్ద కష్టం కాదు. (ఇక్కడ ఉన్న సూక్ష్మం కేవలం కళాశాల కేలుక్యులస్ మాత్రమే పరిచయం ఉన్న వారికి అర్థం కాకపోవచ్చు. దీనికి కారణం ζ(s) రూపం జంట తలం అంతా ఒకేలా ఉండదు; s < 0 అయినప్పుడు దాని రూపు రేఖలు వేరేగా ఉంటాయి. కనుక గుడ్డిగా లెక్క చేసుకుంటూ పోతే అపార్థాలు వస్తాయి.) మూడవ ఉదాహరణగా s = -1 అయితే, ζ(-1) = 1 +2+ 3 + 4 + ... అనగా 1 నుండి నిర్విరామంగా వచ్చే పూర్ణ సంఖ్యలన్నిటిని కూడితే వచ్చే మొత్తం ఎంతో అంత అన్నమాట. అలా దూరం వెళుతూన్న కొద్దీ మొత్తం పెరుగుతూనే ఉంటుంది కదా. ఈ అంక శ్రేణి (arithmetic series) విలువ అనంతం (∞) అవుతుందని అనిపిస్తుంది కాని అలా అవనక్కర లేదని ఇప్పుడు రుజువు చేద్దాం. ఇటువంటి పరిస్థితి ఎదురయినప్పుడు ఫలితం అనంతం (∞) అయితే ఆ చేస్తూన్న లెక్క ఎందుకూ పనికి రాకుండా పోతుంది. ఆ పరిస్థితిని 'ఫలితం పేలిపోయింది' అంటారు. అందుకని ఈ రకం శ్రేణి ఎదురయితే దానికి ముందు ఒక పేరు పెడతారు. ఉదాహరణకి అపసరణం, అగణ్యం, అపశృతం (divergent) వంటి సంస్కృత విశేషణాలు వాడొచ్చు. లేదా - అలవికాని, పత్తా లేకుండా పెడసరించి పెరిగిపోయే, వంటి తెలుగు పదబంధాలు వాడొచ్చు. కనుక మనం కూడ ఈ రకం శ్రేణికి (series) అపసరణ శ్రేణి లేదా అపసృత శ్రేణి లేదా పెడసరించిన శ్రేణి (divergent series) అని పేరు పెడదాం. ఈ విషయం గురించి ఈమాటలో వచ్చిన ఆచార్య సుబ్బరామయ్య మీనాక్షిసుందరం వ్యాసంలో సమబిలిటీ అనే అంశం కింద కొంత చర్చ చూడవచ్చును.

భౌతిక శాస్త్రంలో – ప్రత్యేకించి గుళిక వాదం (quantum theory) లోనూ, పోగుల వాదం (string theory) లోనూ – ఇటువంటి శ్రేణి ఎదురయితే ఏదో పేరు పెట్టేసి తప్పించుకు తిరగడానికి వీలు పడదు. వారు సాధించదల్చుకున్న సమస్యకి పరిష్కారం కావాలనుకుంటే పైన చూపించిన శ్రేణిని కూడగా వచ్చిన మొత్తాన్ని వాడాలి. కాని ఆ మొత్తం అనంతం (∞) అయితే దానిని వాడలేరు. ఏదో ఒక పరిమితమైన సంఖ్యని వాడి రోజు గడుపుకోవాలి. ఏమిటా పరిమితమైన సంఖ్య?

ఇటువంటి పెడసర శ్రేణులని ఎలా మచ్చిక చేసుకుని ఉపయోగించుకోవచ్చో రామానుజన్ (Ramanujan Iyengar) తన నోటుపుస్తకాలలో చెప్పేడు (రామానుజన్ సమ్మేషన్ అంటారు ఈ పద్ధతిని.)

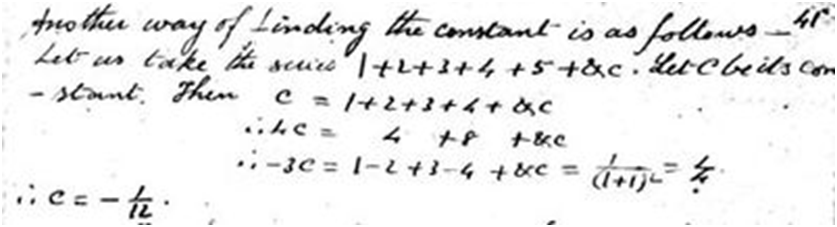
4. అపసృత శ్రేణి గురించి రామానుజన్ వివరణ.

3. రీమాన్ ౙీటా ప్రమేయం విలువ

భౌతిక శాస్త్రవేత్తలకి లెక్కలు లేక పోతే రోజు గడవదు. కాని లెక్కల మేష్టారు చెప్పినట్లు లెక్క చేస్తే ఆశించిన సమాధానం రాకపోతే లెక్క ‘కిట్టించడానికి’ జంకరు. ఈ రకం ‘కిట్టించడం’ అనే ప్రక్రియకి పరిభాషలో, సందర్భానుసారంగా, రెగ్యులరైజేషన్, సమబిలిటీ వగైరా పేర్లు వాడుతూ ఊంటారు. అదే జరిగింది. పైన రాసిన శ్రేణి విలువ ఎంతకి కిట్టించడం? రామానుజన్ నోటు పుస్తకాలలో దీని విలువ – (1/12) అని ఉంది కనుక ఆ విలువ అయితే అన్ని విధాలా నప్పుతుందని ఒకరు అన్నారు. అందరూ సై అంటే సై అన్నారు. అనగా, ఇప్పటి నుండి

S = 1 + 2 + 3 + 4 + ….= – (1/12)

ధన సంఖ్యలన్నిటిని కలిపితే రుణ సంఖ్య ఎలా వస్తుందండీ? కలికాలం కాకపోతే. పూర్ణాంకాలన్నిటినీ కలిపితే భిన్నాంకం ఎలా వస్తుందండీ, విడ్డూరంగా లేదూ?

ఎవ్వరు ఎన్ని అభ్యంతరాలు చెప్పినా ఈ స్థావర జంగమాత్మకమైన సృష్టిలో S = (-1/12) అయితేనే ఈ విశ్వం ఊష్! కాకీ! అంటే ఎగిరిపోయిన కాకిలా ఎగిరిపోకుండా ఏదో ఇలా నడుస్తుందిట. అందుకని ఈ సందర్భంలో అహం దెబ్బ తిన్న ఒక లెక్కల మేష్టారు ఈ కింది విధంగా ఒక రుజువు తయారు చేసేరు.

3.1 ౙీటా ప్రమేయం విలువ: తేలిక పధ్ధతి

ముందు S1 అనే మరొక శ్రేణితో మొదలు పెడదాం.

(పిట్ట కథ: ఈ S1 శ్రేణి విలువ ½ అని కూడ రామానుజన్ నోటు పుస్తకాలలో ఉంది. ఈ రకం అపసరణ శ్రేణిని మొత్తం చెయ్యడానికి ఇది ప్రత్యేకమైన పద్ధతి అని కాని, దీని గురించి ఆయన ఇతర ఆలోచనలు కాని ఏవీ ఆ పుస్తకాలలో లేవు. ఈ రకం కూడిక పద్ధతిని రామానుజన్ పద్ధతి అంటారు. ఇప్పుడు ఈ విలువ భౌతిక శాస్త్రంలో విశ్వాన్ని అర్థం చేసుకునే పోగుల వాదంలో (string theory) చాల ప్రాముఖ్యత వహిస్తోంది.)

S1 = 1 – 1 + 1 – 1 + 1 – 1 + …

ఈ శ్రేణిలో ఒకే ఒక అంశం (పదం) ఉంటే ఆ పాక్షిక మొత్తం (partial sum) విలువ 1. రెండు అంశాలు ఉంటే పాక్షిక మొత్తం విలువ 1 – 1 = 0. మూడు అంశాలు ఉంటే పాక్షిక మొత్తం విలువ 1 – 1 + 1 = 1. అంటే ఏమిటన్న మాట? మనం అనంతం వైపు చేసే ప్రయాణంలో ఈ పాక్షిక మొత్తాలు 0కీ 1కీ మధ్య ఊగిసలాడుతున్నాయి తప్ప ఒక విలువ దగ్గరకి అభిసరించడం (converge అవడం) లేదు. కనుక ‘అనంతం’ వరకు వెళ్ళగలిగితే మొత్తం ఎంత? తుని తగవులా ఇటూ అటూ కాకుండా (1/2) అని ఒప్పేసుకుందాం (రామానుజన్ వెనకాతల దన్నుగా ఉన్నాడనే ధీమాతో). ఈ ఫలితాన్ని ఇంకా రకరకాలుగా సాధించవచ్చు. (కుతూహలం ఉన్న వాళ్ళు ప్రయత్నించండి. ఊహాశక్తి ఉంటే ఉన్నత పాఠశాల విద్యార్థులు ఈ సమస్యని సాధించగలరు!) ఈ ఫలితం తర్వాత మెట్టులో వాడబోతున్నాం.

ఇప్పుడు S2 అనే మరొక శ్రేణిని తీసుకుందాం.

S2 = 1 – 2 + 3 – 4 + 5 – 6 + …

ఈ S2కి మరొక S2ని కలుపుదాం. ఈ కలపడం ఈ దిగువ చూపిన విధంగా, ‘పక్కకి జరిపి’ కలుపుదాం. (రెండూ అనంత శ్రేణులే కనుక ఇలా పక్కకి జరిపి కలపడంలో ప్రమాదం లేదు.)

2S2 = 1 – 2 + 3 – 4 + 5 – 6 + …
           + 1 – 2 + 3 – 4 + 5 – 6 + …

2S2 = 1 – 1 + 1 – 1 + 1 – 1 + … = (1/2)

ఆఖరి మెట్టులో కుడి పక్క వేసిన (1/2) మొదటి మెట్టులో వచ్చిన ఫలితమే!

కనుక 2S2 = (1/2)

లేదా S2 = 1/4

రుజువుని పూర్తి చెయ్యడానికి S నుండి S2ని ఈ దిగువ చూపిన విధంగా తీసివేద్దాం:

S – S2 = 1 + 2 + 3 + 4 + …
           – [1 – 2 + 3 – 4 + 5 – …]

= 0 + 4 + 0 + 8 + 0 + 12 …

1 నుండి 1 తీసేస్తే 0 వచ్చింది. 2 నుండి –2 తీసేస్తే +4 వచ్చింది, అలా ఉంటుందీ లెక్క.

ఇప్పుడు 4ని కుండలీకరణాల బయటకి లాగేసి, దీనిని ఈ దిగువ విధంగా రాయవచ్చు:

S – S2 = 4 (1 + 2 + 3 +…) = 4S

అనగా 3S = – S2.

పైన చేసిన లెక్క ప్రకారం S2 = ¼ కనుక S = – (1/12)

అనగా 1 + 2 + 3 + 4 + … = – (1/12)

ఇదంతా కిట్టించినట్లు కనబడుతోందా? ఈ ఫలితం నమ్మడానికి వీలుగా లేదు కదూ? ధన సంఖ్యలని అలా కలుపుకుంటూ పోతే మొత్తం ధన సంఖ్యే రావాలి. అలా జరగలేదు. పూర్ణాంకాలని అలా కలుపుకుంటూ పోతే ఫలితం పూర్ణాంకమే అవాలి. ఇక్కడ భిన్నాంకం వచ్చింది. అసలు ఈ అంకెలని అనంతం వరకు అలా కలుపుకుంటూ పోతే మొత్తం విలువ పాపం పెరిగినట్లు పెరిగి, పెరిగి, చివరికి ‘పేలిపోవాలి.’ అలా జరగలేదు. కాని మనం చేసిన పద్ధతిలో ఎక్కడా లోపం లేదు.

ఇదే లెక్కని మరికొంచెం పకడ్బందీగా, అంటే కలన గణితం (calculus) ఉపయోగించి, చూపెడతాను. ఈ రుజువు మహా మేధావి ఆయ్‌లర్ చలవ. దీనిని అర్థం చేసుకుందుకి అవకలనంతో (differentiation) కొద్ది పరిచయం ఉంటే చాలు.

3.2 జీటా ప్రమేయం విలువ: దిట్టమైన పధ్ధతి

ఈ దిగువ చూపిన అనంత గుణోత్తర శ్రేణి (geometric series) మొత్తంతో మొదలు పెడదాం. ఈ ఫలితం లెక్కలు నేర్చిన ప్రతి విద్యార్థికీ తెలిసే ఉంటుంది. ఈ విషయం ఇంతకు పూర్వమే తెలిసి ఉండకపోతే మరేమీ ప్రమాదం లేదు; నేను చెబుతూన్నది నిజమే అని నమ్మి ముందుకి కదలండి.

1 + x + x² + x³ + … = 1/(1- x), |x| < 1 ఇక్కడ x విలువ 1 కంటె తక్కువ అయి ఉన్నంత సేపూ ఈ ఫలితం పని చేస్తుంది. ఇప్పుడు అవకలనం (differentiate) చెయ్యడానికి వాడే సూత్రాన్ని ఇక్కడ చెబుతాను. ఇది ఈ రోజుల్లో ఉన్నత పాఠశాలలోనే చెబుతున్నారు. d/dx (xⁿ) = n x^(n-1)

ఇప్పుడు పైన చూపిన అనంత శ్రేణిలోని అంశాలని, ఒకటీ, ఒకటీ అవకలించుకుంటూ పోదాం. ముందుగా స్థిరాంకమైన 1ని అవకలించగా 0 వస్తుంది. x అన్నా x¹ అన్నా ఒక్కటే కనుక అవకలన సూత్రాన్ని బట్టి xని అవకలిస్తే 1 వస్తుంది. అదే విధంగా x²ని అవకలిస్తే 2x వస్తుంది. (ఈ రకం గణితం లెక్కలతో ఏ మాత్రం పరిచయం ఉన్నా తెలుస్తుంది.) ఈ అవకలన సూత్రాన్ని కుడి పక్క కూడా ప్రయోగించాలి. అది ప్రయోగించే విధానం మీద ఒక కప్పదాటు వేస్తే అవకలనం పూర్తి అయిన తరువాత మనకి మిగిలిన సమీకరణం ఈ దిగువ చూపిన విధంగా ఉంటుంది.

0 + 1 + 2 x + 3 x² + ….= 1 / (1-x)(1-x)

ఇప్పుడు x = -1 అనుకుంటే (ఇక్కడ పైన చెప్పిన |x| < 1 అనే నియమాన్ని అతిక్రమిస్తూన్నట్లు కనిపిస్తుంది. వివరణ పాఠకుల ఊహకి వదిలేస్తున్నాం.) 1 – 2 + 3 – 4 + 5 - + ... = ¼ ఈ ఫలితం తరువాత ఉపయోగపడుతుంది. ప్రస్తుతానికి పక్కన పెడదాం. ఇప్పుడు జీటా ప్రమేయాన్ని రంగంలోకి దింపుదాం: ζ(s) = 1^-s + 2^-s + 3^-s + 4^-s + …

దీనిని రెండు పక్కలా 2^-sతో గుణిస్తే: (ఎందుకని అడగకండి. ఇటువంటి గారడీలు కల్పన తలంలో చేసే గణితంలో సాధారణమే. Analytic continuation వంటి మాటలు వాడకుండా అసలు కారణం టూకీగా చెప్పటం కష్టం.)

(2^-s) ζ(s) = (2^-s) (1^-s + 2^-s + 3^-s + 4^-s + …)

కుడిపక్క కుండలీకరణాలని విప్పితే, అంటే, చూపించిన గుణకారాన్ని చేసేస్తే, (ఈ అంచె చెయ్యడానికి బీజగణితంతో కొద్దిగా పరిచయం ఉండాలి)

(2^-s) ζ(s) = 2^-s + 4^-s + 6^-s + 8^-s …

ఇప్పుడు పై సమీకరణాన్ని 2 చేత మళ్ళా గుణించి, వచ్చిన లబ్దాన్ని ζ(s) నుండి తీసేద్దాం. అందరికీ సుబోధకంగా ఉండడానికి ఈ పనిని రెండు అంచెలలో చేద్దాం: ముందు ζ(s)ని ఈ దిగువ విధంగా రాసి, దాని కింద (2^-s) ζ(s)ని తిరగ రాద్దాం.

ζ(s) = 1^-s + 2^-s + 3^-s + 4^-s + …
           = 1 + 2^-s + 3^-s + 4^-s + ….

2 (2^-s) ζ(s) = 2 {2^-s + 4^-s + 6^-s + 8^-s …}

ఇప్పుడు మొదటి సమీకరణం నుండి రెండవ సమీకరణాన్ని తీసివేద్దాం.

(1 – 2 (2^-s) ζ(s)) = 1 + 2^-s + 3^-s + 4^-s + …
                     – 2 {2^-s + 4^-s + 6^-s + 8^-s …}

ఇది పైకి చూడ్డానికి గాభరాగా కనిపిస్తూన్నా ఇక్కడ గణితపరంగా చేసిన బ్రహ్మ విద్య ఏమీ లేదు. ముందు, కుడి పక్క 1 వేసేం. తరువాత పైవరుసలో 2^-s ఉంది, కింది వరుసలో 2^-s రెండు సార్లు రుణ సంజ్ఞతో ఉంది. రెండూ కలపగా మిగిలేది ఒక రుణ సంజ్ఞతో ఉన్న 2^-s. తరువాత పైవరుసలో ఉన్న 3^-sని యథాతథంగా దింపేసుకుందాం. ఇలా చేసుకుంటూ పోతే మిగిలేది:

(1 – 2 (2^-s) ζ(s)) = 1 – 2^-s + 3^-s – 4^-s + …

ఇప్పుడు s = -1 అయితే దీని విలువ ఎంత అవుతుందో లెక్క కడదాం.

కుడిపక్క:

1 – 2⁺¹ + 3⁺¹ – 4⁺¹ + … = 1 – 2 + 3 – 4 + 5 …

ఎడం పక్క:

ఇప్పుడు s = -1 అయినప్పుడు 2^-s కాస్తా 2⁺¹ అవుతుంది. కనుక ఎడం పక్క (1- (2)(2)) ζ(s) = – 3ζ(s). ఇక ఎడం పక్క చెయ్యవలసినదల్లా s = -1 అయినప్పుడు ζ(s) విలువ కూడా కట్టడమే.

ζ(s = -1) = 1 + 2⁺¹ + 3⁺¹ + 4⁺¹ + …
= 1 + 2 + 3 + 4 + 5 + …
– 3 ζ(s = -1) = – 3 (1 + 2 + 3 + 4 + 5 + …)

ఎడమ కుడి చేర్చితే:

– 3 (1 + 2 + 3 + 4 + 5 + …) = 1 – 2 + 3 – 4 + …

కాని ఈ కుడి పక్క ఉన్న అనంత శ్రేణి విలువ (1/4) అని మొట్టమొదటే లెక్కగట్టేం. ఆ విలువ ఉపయోగించి,

– 3 (1 + 2 + 3 + 4 + 5 + …) = ¼

లేదా

(1 + 2 + 3 + 4 + 5 + ….) = – 1/12

ఇందాకటి ఫలితమే వచ్చింది. అందరికీ అందుబాటులో లేని కొద్దిపాటి క్లిష్టత ఉన్న గణితం వాడేం. కనుక ఇప్పుడు ఈ ఫలితం నమ్మడానికి వీలవుతుందా?

మొదటి భాగంలో ఇచ్చిన రుజువులో లోపం ఏదీ లేదు కానీ ఏదో లోపం ఉందేమో అని అనిపిస్తుంది. ఈ రెండవ భాగంలో ఇచ్చిన రుజువు మరికొంచెం పకడ్బందీగా ఉన్నట్లు కనిపిస్తుంది. ఏ రుజువు నచ్చితే దానినే తీసుకోండి. గణితంలో ప్రవేశం అత్యల్పంగా ఉన్న వారికి మొదటి రుజువు చాలు. ఏదో వానాకాలపు కేలుక్యులస్ వరకు చదువుకున్నవారికి ఈ రెండవ రుజువు పని చేస్తుంది.

ఇంత ప్రయాసపడి ఎందుకు ఈ రుజువులు ఇక్కడ చూపించేమూ? ఒకే ఒక్క బిందువు, అనగా s = 1 దగ్గర, ఈ ప్రమేయం అనంతం అవుతుంది తప్ప మిగిలిన జంట తలంలో మరెక్కడైనా సరే ζ(s) విలువ నిర్ధారించడం సాధ్యమే అని రుజువు చెయ్యడానికి. (ఈ పద్ధతి రీమాన్ చలవ!)

4. రీమాన్ ప్రమేయం యొక్క శూన్యాలు

మిలియను డాలర్లు గెలుచుకోడానికి మీ రుజువు బాణసంచాలతో మిలమిల మెరవాలంటే శాఖాచంద్రన్యాయంలా దారి చూపెడతాను. అనగా, ఆకాశంలో చంద్రుడు ఎక్కడున్నాడు? అని అడిగితే, అదిగో! ఆ చెట్టు కొమ్మ వెంబడే చూడు! అని గురువు చెప్పగలడు కాని చంద్రుడి దగ్గరకి చెయ్యి పట్టుకుని తీసుకెళ్ళలేడు కదా. అలాగే ఆ దూరం మీతో ప్రయాణించే ఓపిక, స్థోమత నాలో లేవు. కాసుకోండి!

ముందుగా గౌస్, లెజాండర్ల పద్ధతులని మెరుగు పరచడానికి రీమాన్ ఒక సూత్రసమీకరణాన్ని తయారు చేసేడు. ఆ సూత్రం మనం ఇచ్చిన అవధికి లోపుగా ఎన్ని ప్రధాన సంఖ్యలు ఉన్నాయో చెప్పి, అప్పుడు మనకి కావలసిన సమాధానం ‘అసలు సత్యం’ నుండి ఎంత దూరం మేరకు ‘ఊగిసలాడుతూ ఉండవచ్చో’ కూడ చెబుతుంది. సూత్రసమీకరణంలో ఈ విధంగా ప్రకంపనాల డోలాయమానం గురించి చెప్పే భాగం ౙీటా ప్రమేయం యొక్క సున్నల (zeros of Riemann function) విలువల మీద ఆధారపడి ఉంటుంది. కనుక ఒక ప్రమేయం యొక్క శూన్యాల గురించి కొంచెం తెలుసుకుందాం.

ఏదైనా ఒక ప్రమేయాన్ని, f(x) ని, ఇచ్చి దాని శూన్యాలు (zeros) కనుక్కోమంటే మనం చెయ్యవలసిందల్లా f(x) = 0 అని రాసి, x ఏ విలువ తీసుకుంటే ఈ సమీకరణం చెల్లుతుందో లెక్క కట్టాలి. ఆ x విలువలు ఆ సమీకరణానికి శూన్యాలు అవుతాయి. ఉదాహరణకి f(x) = x – 2 అయితే x = 2 అయినప్పుడు f(x) = 0 చెల్లుతుంది. కనుక x = 2 అనేది f(x) = x – 2 = 0 అనే ప్రమేయానికి శూన్యం అవుతుంది. మరొక ఉదాహరణగా, f(x) = x³ + 2x² -13x + 10 అయితే x = 1 అయినా, x = 2 అయినా, x = -5 అయినా f(x) = 0 చెల్లుతుంది. కనుక x = 1, x = 2, x = – 5 అనేవి f(x) = x³ + 2x² -13x + 10 = 0 అనే ప్రమేయానికి శూన్యాలు అవుతాయి. ఈ శూన్యాలని మూలాలు (roots) అని కూడ అంటారు.

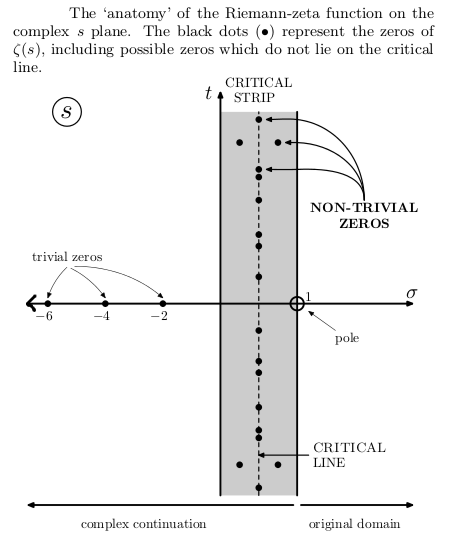
2. రీమాన్ జీటా ప్రమేయం శూన్యస్థానాలు, కీలక రేఖ, కీలక బద్దీ

ఇప్పుడు మనకి కావలసినది రీమాన్ నిర్వచించిన జీటా ప్రమేయం యొక్క శూన్యాలు. జీటా ప్రమేయానికి s = – 2, – 4, – 6, – 8,….. వగైరాలన్నీ శూన్యాలని మనం ఓపికగా లెక్క కట్టి నిర్ణయించవచ్చు అని చెప్పుకున్నాం. అనగా, ζ(s = – 2) = ζ(s = – 4) = ζ(s = – 6) = … = 0. ఇవి మన ప్రస్తుత అవసరాలకి పనికిరావు. కనుక వీటికి ‘పనికిమాలిన’ లేక అల్పశూన్యాలు (trivial zeros) అని పేరు పెట్టి పక్కన పెడదాం. మిగిలినవన్నీ ‘పనికొచ్చే’ లేక కార్యకార శూన్యాలు (nontrivial zeros.) మనకి తెలుసున్నంత వరకు, ఈ కార్యకార శూన్యాలు అన్నీ s = ½ + b i అనే రేఖ మీదనే ఉన్నాయి. ఈ రేఖ జంట తలంలో కల్పన అక్షానికి సమాంతరంగా, నిజ రేఖ మీద 1/2 దూరంలో గీసిన గీత (బొమ్మ 5 చూడండి). రీమాన్ వ్యక్తపరచిన శిష్టాభిప్రాయం ఏమిటంటే కార్యకార శూన్యాలు s = ½ + bi అనే ఈ కీలక రేఖ (critical line) మీద తప్ప మరెక్కడా ఉండవని. కీలక బద్దీ (critical strip) మీద ఉంటే సరిపోదు; కీలక రేఖ మీద తప్ప మరెక్కడా ఉండకూడదు. ఈ విషయం రుజువు చెయ్యాలి.

జీటా ప్రమేయం యొక్క సున్నా విలువలన్నీ కీలక రేఖ మీదే ఉన్నాయనిన్నీ, మరెక్కడా లేవనిన్నీ మనకి ఖచ్చితంగా తెలిస్తే రీమాన్ ఇచ్చిన ఫార్ములాలో ‘సత్యం నుండి ప్రకంపనాల డోలాయమాన దూరాన్ని అంచనా వేసే భాగాన్ని’ నమ్మ వచ్చు. సున్నాలు ఇంకెక్కడైనా ఉండే అవకాశం పొంచి ఉన్నంత కాలం శ్రీమాన్ రీమాన్ వారి సూత్రం (formula for prime number count) ఇవ్వాలనుకున్న ఫలితాన్ని ఖచ్చితంగా ఇవ్వజాలదు.

5. ఆసక్తికరమైన విషయాలు

5. 1 రామానుజన్, హార్డీ

రీమాన్ వ్యక్తపరచిన శిష్టాభిప్రాయానికి ఒక రకమైన రుజువుని 1914లో హార్డీ కనుక్కున్నాడు. (రామానుజన్ హార్డీకి రాసిన మొదటి ఉత్తరం 1913లో అని మరచిపోకండి.) హార్డీ పైన చెప్పిన s = ½ + bi అనే కీలక రేఖ మీద ζ(s)కి అనంతమైనన్ని శూన్యాలు ఉన్నాయని రుజువు చేసేరు కాని s = 0 + bi నుండి s = 1 + bi వరకు ఉన్న కీలక బద్దీలో (critical strip) మరే శూన్యాలు పొంచి ఉండలేదని రుజువు చెయ్యలేదు. కనుక హార్డీ కనుక్కున్న రుజువు రీమాన్ సమస్యకి పరిష్కారం కాదని తేలిపోయింది.

రామానుజన్‌తో పరిచయం అయిన తరువాత హార్డీ తెలుసుకున్నది ఏమిటంటే రీమాన్ సాధించిన ఫలితాలు దరిదాపుగా అన్నీ రామానుజన్ నోటు పుస్తకాలలో ఉండడం. రామానుజన్ గురుముఖంగా ఏదీ నేర్చుకోలేదు. రామానుజన్‌కి అంత వరకు గణిత ప్రపంచంలో ఏమిటి జరిగిందో తెలియదు. అయినా సరే రీమాన్‌కి తెలిసిన విషయాలన్నీ రామానుజన్‌కి తెలిసే ఉండాలి. కనుక రీమాన్ ప్రతిపాదించిన సమస్య పరిష్కారానికి కావలసిన స్థోమత రామానుజన్ దగ్గర ఉండే ఉండాలి. అప్పటికే ఈ సమస్యతో కుస్తీ పడుతున్న హార్డీ ఈ విషయాన్ని రామానుజన్‌తో ముచ్చటించే ఉండాలి. రామానుజన్ కూడ ఈ సమస్య పరిష్కరించడానికి ప్రయత్నం చేసేడేమో. కాని ఒకటి మాత్రం నిజం. రీమాన్ సమస్యని కొంతవరకు పరిష్కరించిన తరువాత హార్డీ మనోవ్యాకులతకి లోనై మాత్రలు మింగి ఆత్మహత్య చేసుకుందుకి ప్రయత్నం చేసేడు. లండన్‌లో ఉన్న రోజులలో రామానుజన్ కూడ మనోవ్యాకులతకి లోనై రైలుబండి కింద పడి చచ్చిపోడానికి ప్రయత్నం చేసేడు. అదృష్టవశాత్తు ఇంజనీరు బండికి బ్రేకు వేసి ఆపగలిగేడు కనుక రామానుజన్ గండం నుండి బయట పడ్డారు. ఈ రెండూ కేవలం కాకతాళీయం కావచ్చు, ఈ రెండు సంఘటనలకి రీమాన్ సమస్యని పరిష్కరించడానికి వీరిరువురు చేసిన ప్రయత్నాలకి మధ్య ఉన్నది బాదరాయణ సంబంధమే కావచ్చు. కాని ఈ సమస్యే వీరి మతిని చలింపజేసిందని అభిజ్ఞ వర్గాల్లో అనుకున్న వాళ్ళు లేకపోలేదు.

5.2 నా శిష్టాభిప్రాయం ఒకటి!

ఇంత రాసినాక కూడా నేను కూడ ఒక శిష్టాభిప్రాయం వెలిబుచ్చుతాను. నా విద్యార్థి దశ ఇంకా లేతగా ఉన్న రోజులలో ఒక వ్యవస్థ స్థిరత్వం (stability of a system) గురించి విచారణ చేసేటప్పుడు ఒక బహుపది (polynomial) శూన్యాలు ఎక్కడ ఉన్నాయో తెలుసుకోవడం ఒక కీలకమైన అంశంగా ఉండేది. ఈ శూన్యస్థానాల విలువలు గణన చేసి కనుక్కోవడం తేలిక కాదు. అందుకని అవి జంట తలంలో కల్పన రేఖకి ఎడం పక్క ఉన్నాయో, కుడి పక్క ఉన్నాయో ముందు అంచనా వేసే వాళ్ళం. కుడి పక్క ఉంటే గోవిందా! ఎడం పక్క ఉంటే, అవి నిజ అక్షం మీదనే ఉన్నాయా, లేక జంట తలంలో అక్కడక్కడ జంటలుగా (conjugate pairs) ఉన్నాయా అన్న విషయం తెలిస్తే అప్పుడు ఆ వ్యవస్థ నిశ్చలత గురించి వ్యాఖ్యానం చెయ్యవచ్చు. నిశ్చలత అంటే? ఆ వ్యవస్థని కదిలిస్తే విరామ స్థలం నుండి ఎలా ‘ఊగిసలాడుతుందో,’ ఎంతసేపు ఊగిసలాడుతుందో తెలుసుకోవడం. ఇదంతా విరళ (non-linear) సమీకరణాలకి అనువర్తించదు. రీమాన్ పద్ధతిని ఈ సందర్భంలో వాడి విరళ వ్యవస్థల స్థిరత్వం అధ్యయనం చెయ్యగలిగితే ప్రధాన సంఖ్యల ‘ఉపయోగం’ యొక్క పరిధి విపరీతంగా పెరుగుతుంది.

[కృతజ్ఞత: ఈ వ్యాసాన్ని నలుగురి చేత పునరావలోకనం చేయించి, వారి అభిప్రాయాలని సేకరించి నాకు అందచేసిన సంపాదకులకి, చదివి సలహాలు ఇచ్చిన సహాధ్యాయులందరికీ హృదయపూర్వక ధన్యవాదాలు. ప్రత్యేకించి రాజా పిడూరి గారు తీసుకున్న శ్రద్ధకీ, వెచ్చించిన సమయానికీ ఎంతగానో కృతజ్ఞుణ్ణి. వారి సహకారం వల్ల ఈ వ్యాసం ఎంత మెరుగుపడిందో మాటల్లో చెప్పలేను – ర.- ]

ఆధారాలు

1. du Sautoy, Marcus, The Music of the Primes: Searching to Solve the Greatest Mystery in Mathematics. ISBN 0-066-21070-4. HarperCollins. 2003.
2. B. Riemann, “Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse,” (“On the Number of Prime Numbers Less Than a Given Quantity”), Monatsberichte der Berliner Akademie (Monthly Review of the Berlin Academy), November 1859.
3. Ramanujan wrote in his second letter to G. H. Hardy, dated 27 February 1913:

   “Dear Sir, I am very much gratified on perusing your letter of the 8th February 1913. I was expecting a reply from you similar to the one which a Mathematics Professor at London wrote asking me to study carefully Bromwich’s Infinite Series and not fall into the pitfalls of divergent series. … I told him that the sum of an infinite number of terms of the series: 1 + 2 + 3 + 4 + · · · = −1/12 under my theory. If I tell you this you will at once point out to me the lunatic asylum as my goal. I dilate on this simply to convince you that you will not be able to follow my methods of proof if I indicate the lines on which I proceed in a single letter. …”

4. Thomas Wright, A Friendly Introduction to the Riemann Hypothesis.(PDF)